近期省选题思路整理

「过难」的定义是目前洛谷上通过人数 19/20 年 \(100\) 左右（或更少），18 年 \(200\) 左右（或更少）的黑题 （因为早年题做的人多）

「过水」的定义是我不用思考就直接会做的题目

「过偏」的定义是考察点大概率不会出现/过于奇葩，没有做的意义的题目

标记了 AC 的题目代表写了代码；没标的代表没写代码，只是看了思路

因为众所周知 AH 是山区 ，所以太难的题目就不做了（

每道题目的关键思想/算法加粗。

2020

• P6619 [省选联考 2020 A/B 卷] 冰火战士 AC
  求的是两个单调函数的 \(\min\)，本质上是单峰函数。
  三分法对非严格单峰函数不适用，可以换成二分+二分。
  树状数组套二分或许可以换为直接在树状数组上二分，\(O(\log^2 n) \to O(\log n)\)。
• P6620 [省选联考 2020 A 卷] 组合数问题 AC
  组合恒等式 \(k\binom{n}{k}=n\binom{n-1}{k-1}\)。
  可以在下降幂形式上推广：\(k^{\underline l} \binom{n}{k} = n^{\underline l} \binom{n - l}{k - l}\)。
  普通多项式转下降幂多项式：\(x^k = \sum\limits_{i=0}^{k} \left\{ \begin{matrix} k \\ i \end{matrix} \right\} x^{\underline i}\)。
• P6621 [省选联考 2020 A 卷] 魔法商店 过难
• P6622 [省选联考 2020 A/B 卷] 信号传递 AC
  状压 DP，要懂得可以把两者之间的贡献分拆到两者身上去计算。
  经典结论：\(1 \sim n\) 的比特位的变化是 \(O(n)\) 的。
• P6623 [省选联考 2020 A 卷] 树 AC
  异或要尝试用 trie 去维护。
  全局 \(+1\) 这种与低位有关的操作可以尝试从低位到高位建 trie。
  trie 合并和线段树合并的复杂度都是均摊 \(O(\log n)\) 的。
• P6624 [省选联考 2020 A 卷] 作业题 AC
  生成树一类的计数一定要考虑 Matrix-tree 定理。
  看到 \(\gcd\) 上来一定要反演。
  矩阵维护一次多项式来统计贡献，本质上是出于 OGF 的考虑，并不影响行列式的计算。
  \(\bmod x^2\) 下的多项式除法一类的推导，可以用设逆元然后解方程的方式。
• P6625 [省选联考 2020 B 卷] 卡牌游戏 过水
• P6626 [省选联考 2020 B 卷] 消息传递 AC
  裸的点分治，注意同时均摊复杂度处理所有的询问。
• P6627 [省选联考 2020 B 卷] 幸运数字 AC
  异或也可以差分。
• P6628 [省选联考 2020 B 卷] 丁香之路 AC
  神仙推性质题。
  这类构造环的问题以后可以考虑从点的度数下手，毕竟环的本质是欧拉回路。
• P6629 [ZJOI2020] 字符串 过难
• P6630 [ZJOI2020] 传统艺能
  线段树操作时候点可以分为五类（图是 Sooke 的）
  
  对于这五类点分别设计转移方程就很显然，处理其他问题也要考虑将对象分类。
• P6631 [ZJOI2020] 序列 AC
  注意到最边上的点的处理是显然的，可以从这里入手。
  “预留” 的思想也很有用。
• P6632 [ZJOI2020] 染色游戏 过难
• P6633 [ZJOI2020] 抽卡 过难
• P6634 [ZJOI2020] 密码 过难
• P6640 [BJOI2020] 封印 AC
  SA 处理 lcp 的方法是将两个字符串拼在一起进行后缀排序。
  \(\text{Height}\) 数组求出来以后用 ST 表维护一下即可。
• P6790 [SNOI2020] 生成树 过难
• P6791 [SNOI2020] 取石子 AC
  博弈问题如果推不出来可以考虑打表。
  打表了以后 Fibonacci 数列就很显然了。
  值得注意的是可能区间可以平移，也就是将贡献区间分段的话，后面的段可能可以等价地平移到开头。
• P6792 [SNOI2020] 区间和 过难
• P6793 [SNOI2020] 字符串 AC
  将修改问题转化为匹配问题，套路地将 \(a, b\) 拼起来后缀排序。
  接下来就可以分治处理，即内部匹配完了以后，将剩余的子串返回到上一层进行匹配。
• P6794 [SNOI2020] 水池 过难
• P6795 [SNOI2020] 排列 过难

2019

• P5279 [ZJOI2019] 麻将 过偏（dp 套 dp）
• P5280 [ZJOI2019] 线段树
  同 P6630 [ZJOI2020] 传统艺能。
• P5281 [ZJOI2019] Minimax 搜索 过偏（动态 dp）
• P5283 [十二省联考 2019] 异或粽子 AC
  使用堆对于每一个右端点，维护左端点的集合。
  每次取出一个数以后进行区间分裂，只会增加至多 \(1\) 个区间，因此堆中的元素个数保持 \(O(n)\) 级别。
  对于区间的异或最大值，可以使用可持久化 trie 树来维护。
• P5284 [十二省联考 2019] 字符串问题
  后缀排序以后很显然需要建图，因为是区间往点连边的形式，所以需要使用线段树优化建图。
  但是因为有长度的限制，所以可以根据长度，将线段树改造为可持久化线段树优化建图，套用线段树优化建图的方式即可。
  代码太长了 /tuu
• P5285 [十二省联考 2019] 骗分过样例 过偏（看数据找规律）
• P5286 [HNOI2019] 鱼
  完全口胡，计算几何应该不会考吧。
  枚举 \(D\)，其他点极角排序。
  枚举 \(A\)，双指针求出鱼尾的数量。
  因为 \(BC\perp AD\)，所以把 \(BC\) 按照斜率分类，每一类再按照中点分类，终点必须在 \(AD\) 上。
  鱼身和鱼尾相乘后相加，\(\times 4\) 得到答案。
• P5287 [HNOI2019] JOJO
  考察对 KMP 的深层次理解。
  可持久化可以离线下来变成回退。
  每次增加一段字符的时候，其实就是要从之前最后一个字符开始跳 \(nxt\) 跳到一个位置后面有连续 \(y\) 个 \(c\)。
  因为 \(c\) 不等于之前最后一个字符，所以如果跳到了一段中间的话是肯定没有用的。
  所以定义 \(nxt_i '\) 表示从第 \(i\) 个字段的最后一个点开始，一直跳 KMP 的 \(nxt\)，跳到的第一个位于某个字段末端的点。
  每次跳 \(nxt_i '\) 时，考虑：
  \(\circ\) 如果当前字符串存在周期，那么跳到所有周期的第一个。
  \(\circ\) 否则，直接跳到 \(nxt'\)。
  不难发现每次操作都使得长度 \(/2\)，复杂度 \(O(n \log n)\)。
• P5288 [HNOI2019] 多边形 过难
• P5289 [十二省联考 2019] 皮配 AC
  观察到阵营和派系的安排其实是独立的，对于没有限制的学校可以分别 DP 后乘起来。在 \(O(nm)\) 的复杂度内得到两个一维数组。
  对于有限制的，因为个数很少，所以可以对阵营和派系分别设计维度来二维 DP。这部分是 \(O(kM^2)\) 的，稍微卡一下上界就是 \(O(k^2 sM)\) 的。
  最终合并统计答案。
• P5290 [十二省联考 2019] 春节十二响 AC
  对一棵子树求解时，开的段数肯定是深度个。
  使用堆启发式合并两棵子树的答案，因为每次合并都会少一个点，总复杂度是 \(O(n \log n)\) 的。
• P5291 [十二省联考 2019] 希望 过难
• P5292 [HNOI2019] 校园旅行
  首先考虑一个简单的 \(O(m^2)\) 的 DP，也就是用 \(f(u, v)\) 表示 \(u, v\) 之间是否存在一条合法路径，转移显然。
  考虑减少边数：
  \(\circ\) 对于一个同色连通块，如果是二分图，那么保留一棵生成树就行了；否则找一个点连一条自环。
  \(\circ\) 将同色连通块缩点后，剩下的连接异色的边必然是二分图，保留一棵生成树即可。
  于是就把边数压到了 \(O(n^2)\) 的级别。
• P5293 [HNOI2019] 白兔之舞 过偏（多项式 + 单位根反演）
• P5294 [HNOI2019] 序列 过难
• P5300 [GXOI/GZOI2019] 与或和 AC
  对于求“全 \(1\)”一类的矩阵可以考虑单调栈。
  使用单调栈维护矩形即可。
• P5301 [GXOI/GZOI2019] 宝牌一大堆 过偏（大 D P）
• P5302 [GXOI/GZOI2019] 特技飞行 过难
• P5303 [GXOI/GZOI2019] 逼死强迫症 AC
  枚举两个 \(1 \times 1\) 的矩阵就会发现中间的方案唯一。
  答案形如 \(Ans(x) = \sum_\limits{i + j \le x} F(i) F(j)\)。
  矩阵优化转移。
• P5304 [GXOI/GZOI2019] 旅行者 AC
  看到最短距离可以考虑枚举一个中间边然后把最短路拆开。
  正反跑两遍 Dijkstra，分别染色。
  枚举中间边求答案即可。
• P5305 [GXOI/GZOI2019] 旧词
  将操作离线下来按照 \(x\) 排序。
  每次插入一个点 \(u\) 时，把 \(u\) 到根的路径上每个点权 \(+ \left(dep^k - (dep - 1)^k\right)\)。
  询问的时候查 \(u\) 到根的权值和即可。
  树链剖分随便维护。
• P5319 [BJOI2019] 奥术神杖 AC
  乘积类型的东西明显炸 long long 的，很可能是取 \(\ln\) 以后变成求和。
  最大化 \(\frac{1}{c} \sum\limits_{i=1}^{c} w\) 是经典的 \(0/1\) 分数规划问题。
  多串匹配惯例使用 AC 自动机。
• P5320 [BJOI2019] 勘破神机 过偏（多项式）
• P5321 [BJOI2019] 送别 过难
• P5322 [BJOI2019] 排兵布阵 过水
• P5323 [BJOI2019] 光线
  一种做法是合并玻璃，等效替代；另一种做法是设方程组然后递推。
• P5324 [BJOI2019] 删数
  不难抽象为数轴上 \(v\) 这个点立着一根长为 \(cnt_v\) 的木棍，修改即是移动任意一个单位长度。
  答案很明显就是所有木棍倒下来后，空位置的个数。
  整体操作使用平移原点的方法。
  因此可以使用线段树维护。
• P5326 [ZJOI2019] 开关 过偏（生成函数 / FWT）
• P5327 [ZJOI2019] 语言
  给定树上若干个点，求其最小斯坦纳树：先假定加入 \(u_1 = 1\)，把给定的点按照 DFS 序排序，答案即为 \(\sum\limits_{i=1}^{k} dep(u_i) - \sum\limits_{i=2}^{k} dep(\text{LCA}(u_{i-1}, u_i)) - dep(\text{LCA}(u_2, u_3, \cdots, u_k))\)。
  使用线段树维护的话，叶子节点 \(tag = 0/1\) 代表其被不被选，辅助维护某一段区间的第一个 \(1\) 的位置和最后一个 \(1\) 的位置即可。
  对于链的修改可以树上差分，继承信息直接线段树合并。
• P5328 [ZJOI2019] 浙江省选 过难
• P5329 [SNOI2019] 字符串 过水
• P5330 [SNOI2019] 数论
  模意义下的数一般要考虑其周期性。
  考虑枚举 \(A\)，预处理 \(kP+b\) 在 \(\bmod Q\) 下的循环情况，前缀和优化即可。
• P5331 [SNOI2019] 通信
  点数不多，所以考虑使用费用流。
  优化建图可以使用累加权值之差的方式。
• P5332 [JSOI2019] 精准预测
  生、死作为两种对立的状态，考虑 2-SAT 模型。
  接下来使用 bitset 压位，求出一个 \(T+1\) 时刻的生点能到达几个 \(T+1\) 时刻的死点即可。
• P5333 [JSOI2019] 神经网络 过难
• P5334 [JSOI2019] 节日庆典 过难
• P5337 [TJOI2019] 甲苯先生的字符串 过水
• P5338 [TJOI2019] 甲苯先生的滚榜 AC
  平衡树维护一个 pair，按照题目说的模拟就行了。
• P5339 [TJOI2019] 唱、跳、rap和篮球 AC
  几个点作为一个整体计数的问题可以考虑把他们缩成一个点来看。
  二项式反演的一种形式：\(f(k) = \sum\limits_{i=k} \binom{i}{k} g(i) \Leftrightarrow g(k) = \sum\limits_{i=k} (-1)^{i-k} \binom{i}{k} f(i)\)。
  \(k\) 个同种颜色的 EGF 是 \(f_k(x) = \sum\limits_{i=0}^{k} \frac{x^i}{i!}\)，卷起来表示带标号乱序插入，就可以得到答案。
• P5340 [TJOI2019] 大中锋的游乐场 AC
  按照两者的差值分层跑最短路即可。
• P5341 [TJOI2019] 甲苯先生和大中锋的字符串
  建出 SAM，统计每个结点的 \(|\text{endpos}|\)，然后对于所有大小为 \(k\) 的结点，将其代表的长度区间 \(+1\) 差分维护即可。
• P5342 [TJOI2019] 甲苯先生的线段树 过难
• P5358 [SDOI2019] 快速查询
  本质不同的询问并不多，所以可以把实际用到的下标存起来离散化。
  对于每一个位置维护一个加法标记和一个乘法标记，单点赋值的时候解方程赋一个适应当前标记的等价值即可。
• P5359 [SDOI2019] 染色 过难
• P5360 [SDOI2019] 世界地图 过难
• P5361 [SDOI2019] 热闹的聚会与尴尬的聚会 AC
  题目的要求其实就是 \(p, q\) 都尽可能大。
  对于第一问，每次删去图中度数最小的点并更新答案即可。
  对于第二问，最大独立集是 NP 的，但这题并不是一定要求最大的，只要尽量大即可。
  于是考虑两问的联系，每次找度数最小的点加入独立集，并把它周围点都删掉。
  因为每次至多删掉 \(p\) 个点，所以 \(q \ge \lfloor\frac{n}{p+1}\rfloor\)。
  注：一般最大独立集问题的随机做法：随机一个排列然后从前往后贪心选点。
• P5362 [SDOI2019] 连续子序列 过偏（找规律）
• P5363 [SDOI2019] 移动金币 AC
  阶梯 Nim 游戏的先手必胜条件：从末端开始编号 \(0, 1, 2, 3 \cdots\)，要求 \(a_0 \oplus a_2 \oplus a_4 \cdots \ne 0\)。
  于是这题考虑枚举每一个比特位出现的次数（偶数次），做一个类似背包的 DP 即可。
• P5371 [SNOI2019] 纸牌
  注意到等价性，如果 \((x-1,x,x+1)\) 出现超过了 \(3\) 次，则完全可以理解为 \(3(x-1)+3x+3(x+1)\)。
  所以 \(f_{i, j, k}\) 表示前 \(i\) 种牌，有 \(j\) 个 \((i-2, i-1)\)，额外还有 \(k\) 个 \((i-1)\)，有意义的状态 \(j, k < 3\)。
  这种轮廓线 DP 的思想也很常用，使用矩阵快速幂优化空档转移即可。
• P5372 [SNOI2019] 积木 过偏（纯构造，也没啥人写）
• P5411 [SNOI2019] 网络 过难
• P5412 [YNOI2019] 排队 过水
• P5413 [YNOI2019] 骑单车 过水
• P5414 [YNOI2019] 排序 过水
• P5415 [YNOI2019] 游戏
  概率 DP 可以考虑列出各量之间的关系，然后高斯消元求解。

2018

• P4337 [ZJOI2018] 线图 过难
• P4338 [ZJOI2018] 历史 过偏（LCT）
• P4339 [ZJOI2018] 迷宫 过难
• P4363 [九省联考 2018] 一双木棋 AC
  博弈问题中，如果一方想最大化某值，另一方想最小化某值，可以考虑 Min-Max 对抗搜索。
  而优化 Min-Max 对抗搜索的常用方法就是记忆化。
  这题状态压缩的方法很巧妙，以后可以考虑用构造全 \(0\) 基量中插入 \(1\) 的方式来状压。
• P4364 [九省联考 2018] IIIDX
  最小化/最大化字典序，一般都是从 \(1\) 开始贪心。
  每个位置放有机会放的最大的数，同时把剩下那部分预留起来。
  预留的实现可以是线段树维护前缀个数 \(\min\)，修改变为单点修改，查值则是线段树二分。
• P4365 [九省联考 2018] 秘密袭击 过偏（多项式 + 线段树合并 + 整体 DP）
• P4382 [八省联考 2018] 劈配
  对于第一问，依次加入第 \(k\) 志愿的边后在残量网络上跑 Dinic，如果存在增广路了就退出
  对于第二问，二分答案 \(mid\)，将前 \(mid\) 个人按照最优方案建图，然后加入第 \(i\) 个人理想的边，跑 Dinic 即可。
  多次建图的复杂度过高，可以直接把前 \(i\) 个人的最优情况的残量图都存下来。
• P4383 [八省联考 2018] 林克卡特树 过偏（wqs 二分/带权二分/DP 凸优化）
• P4384 [八省联考 2018] 制胡窜 过难
• P4424 [HNOI/AHOI2018] 寻宝游戏 AC
  二进制位运算考虑逐位分析。
  把操作中的 \(\land\) 和 \(\lor\) 也看作 \(0/1\) 的话，发现，令操作串代表的数为 \(opt\)，则每一位都是一个 \(opt \le x\) 或 \(opt > x\) 的不等式。
  解这个不等式，解的个数就是答案。
• P4425 [HNOI/AHOI2018] 转盘
  观察到，如果一个点被访问了两次及以上，那么第一次访问毫无意义。
  也就是，可以理解为，在起点等待一段时间，然后完整地走一圈。
  破环为链，枚举起点 \(i\)（\(1 \le i \le n\)），\(Ans = \max\limits_{i \le j < i+n} \left\{ T_j - (j - i) \right\} + (n - 1)\)。
  \(\Rightarrow Ans = (n - 1) + \max\limits_{i \le j \le 2n} \left\{ T_j - j \right\} + i\)。
  于是使用线段树维护单调栈，这是经典的楼房重建模型。
• P4426 [HNOI/AHOI2018] 毒瘤
  普通树的独立集 DP 就是看 \(u\) 选还是不选，\(f(u, 0) = \prod f(v, 0)+f(v, 1); f(u, 1) = \prod f(v, 0)\)。
  接下来枚举每一条非树边是 \((0, 0)\) 还是 \((1, 0)\) 还是 \((0, 1)\)，注意到 \((0, 0)\) 和 \((0, 1)\) 是可以合并的，那么就直接枚举上侧点选不选了，时间复杂度 \(O(2^{m-n}n)\)。
  每次跑 \(n\) 个点的 DP 是很浪费时间的，所以把关键点拉出来建虚树，预处理出转移式中的系数，复杂度就是 \(O(2^{m-n}(m-n))\) 了。
• P4427 [BJOI2018] 求和 AC
  \(k\) 很小，而且不带修，那么对每一种 \(k\) 分别预处理，查询时倍增即可。
• P4428 [BJOI2018] 二进制 过难
• P4429 [BJOI2018] 染色 过难
• P4436 [HNOI/AHOI2018] 游戏 AC
  门一定是单向的，所以图肯定构成一个 DAG，拓扑排序后依次继承式扩散区间，即可把时间复杂度降到 \(O(n)\)。
• P4437 [HNOI/AHOI2018] 排列
  容易得知的性质是形如“选了 \(\textit{fa}(i)\) 下一个一定会选 \(i\)”，所以每次贪心将 \(\textit{fa}(i)\) 和 \(i\) 合并即可。
  至于先选哪个数，使用邻值交换法推导即可。
• P4438 [HNOI/AHOI2018] 道路 AC
  因为 \(dep \le 40\)，干脆把 \(x, y\) 设计到状态里。
  接下来对于每一个 \(u\) 讨论翻修他下方的哪条路，做一个小 DP 即可。
  这题竟然卡空间，要动态开空间。
• P4454 [CQOI2018] 破解 D-H 协议
  原根与 \(P\) 互质。
  求解 \(g^x \equiv A \pmod{P}\) 可以考虑使用 BSGS。
• P4455 [CQOI2018] 社交网络
  求有向图以 \(1\) 为根的叶向树形图的个数。直接上 Matrix-tree 定理就好了。
  \(T^{\textit{leaf}}=\operatorname{Det}(L'^{\textit{in}}),T^{\textit{root}}=\operatorname{det}(L'^{\textit{out}})\)。
  理解：叶向树形图就是每个点选一条入边构成生成树，根向树形图就是每个点选一条入边构成生成树。
• P4456 [CQOI2018] 交错序列
  消元是一个好思想，也就是把 \(x\) 用 \(n - y\) 表示。
  一般来说，指数很小的时候要尝试把指数设计到状态里面。
  然后就是简单的矩阵优化 DP 了。
• P4457 [BJOI2018] 治疗之雨 题目没看懂
• P4458 [BJOI2018] 链上二次求和
  将答案化为二次函数的形式，使用线段树每个位置维护二次函数的 \(a, b, c\) 值即可。
  注意看清题目有没有保证 \(l \le r\)……
• P4459 [BJOI2018] 双人猜数游戏 过难
• P4460 [CQOI2018] 解锁屏幕
  \(n\) 很小，考虑状压，哈密顿路径式 DP，枚举下一个点的时候加一个限制条件即可。
• P4461 [CQOI2018] 九连环
  \(n\) 连环的最小步骤是 \(\lfloor\frac{2^{n+1}}{3}\rfloor\)。
  高精度 FFT 。
• P4462 [CQOI2018] 异或序列 AC
  看到异或，求前缀和，然后使用莫队维护区间内每种异或值的个数就行了。
• P4491 [HAOI2018] 染色 过偏（二项式反演 + NTT）（希望 CCF 考纲是真的
• P4492 [HAOI2018] 苹果树 AC
  树上距离和可以转化为考虑每一条边被经过的次数。
  \(P\) 不是指数的时候可以尝试把 阶乘除阶乘 改成 组合数乘阶乘 的形式。
• P4493 [HAOI2018] 字串覆盖 过难
• P4494 [HAOI2018] 反色游戏 过偏（圆方树）
• P4495 [HAOI2018] 奇怪的背包
  首先模意义下要寻找循环节，物品 \(v\) 在模 \(P\) 意义下可以等价为 \(\gcd(v, P)\)。
  同理，询问也可以进行等价。所以每次询问就是询问有多少种选若干个数的方案使得 \(\gcd = w\)。
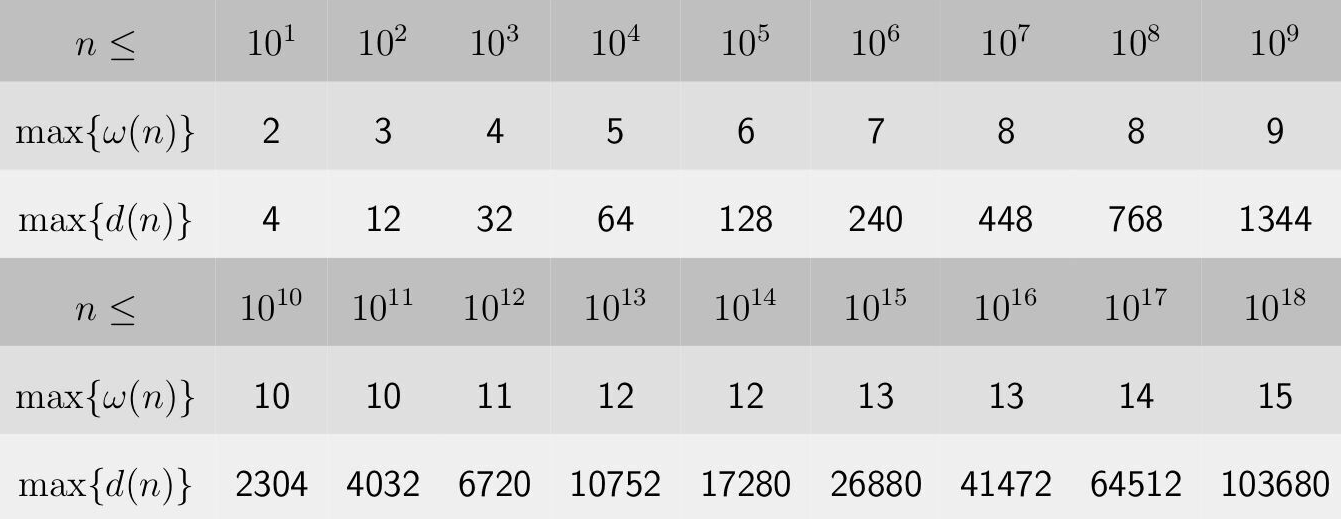
  于是就可以将 \(P\) 质因数分解。
  
  根据这张著名的表知道，本质不同的询问只有 \(10^3\) 级别种，分别预处理即可。
• P4500 [ZJOI2018] 树 过难
• P4501 [ZJOI2018] 胖 过偏（找性质题）
• P4502 [ZJOI2018] 保镖 过难
• P4516 [JSOI2018] 潜入行动
  经典的树形背包，用 \(f(u, i, 0/1, 0/1)\) 表示 \(u\) 这棵子树中选了 \(i\) 个，\(u\) 这个点选没选，\(u\) 这个点有没有被覆盖到，方案数。
  树形背包尽量使用上下界优化，也就是无意义状态要割干净，时间复杂度就是 \(O(nk)\) 的。
• P4517 [JSOI2018] 防御网络 过难
• P4518 [JSOI2018] 绝地反击 过偏（计算几何 + 二分 + 扫描线 + 网络流）
• P4557 [JSOI2018] 战争 过偏（怎么 JSOI 两道计算几何）
• P4558 [JSOI2018] 机器人 过难
• P4559 [JSOI2018] 列队
  看到处理与坐标关联的问题，可以考虑使用权值线段树来维护。
  而这题还有标号的限制，故需要增加一个维度，也就是可以按照标号将权值线段树可持久化。
  一段区间如果全部向右/全部向左就可以直接计算，否则递归。
  显然这样拆分出来的区间个数也是 \(\log\) 级别的。
• P4561 [JXOI2018] 排序问题
  一个关于期望的小结论：每次操作完全相同且随机，成功需要的次数 \(=1/\) 单次操作成功的概率。
  包含相同的元素的排列个数 $ = \frac{n!}{\prod cnt_i !}$。
  最大化下面那个东西其实就是在一个阶梯形的数组上贪心填充。
• P4562 [JXOI2018] 游戏
  问题求的 \(t(p)\) 其实就是 \(p\) 中最后一个“不可以被别人筛掉的数”的出现位置。
  类埃氏筛法可以 \(O(n \log \log n)\) 求出上述数字的个数，然后枚举答案算方案数分别求和即可。
  坑：后 \(n - ans\) 个数也是要乱序排列的！以后一定不能只关心重要部分而漏算了其他部分的贡献。
• P4563 [JXOI2018] 守卫
  看到斜率很容易想到凸包或者单调栈，但是这样就错了（
  对于所有区间都进行询问的题目可以考虑固定 \(l\) 或 \(r\)，移动另一个指针来维护答案。
• P4577 [FJOI2018] 领导集团问题
  树上 LIS 问题，可以考虑类比序列 LIS 问题的做法，对每一个节点开一个 multiset \(f_u\)。
  首先不考虑 \(u\) 本身，\(f_u = \bigcup f_v\)。
  接下来考虑 \(w_u\)，因为 multiset 中本质是维护“当答案为 \(x\) 时的最大转移要求（因为这题是 LDS）”，那么把 \(w_u\) 插入到 \(f_u\) 中后，除非 \(w_u\) 是 \(f_u\) 中最小的一个，否则把 \(w_u\) 的前一个迭代器删除就好了。
  \(f\) 之间的合并要使用启发式合并，时间复杂度是 \(O(n \log^2 n)\) 的。
• P4578 [FJOI2018] 所罗门王的宝藏 AC
  解若干个 \(x + y = z\) 的方程可以拆成 \(x + y \le z, x + y \ge z\)，标准化后使用差分约束算法即可。
• P4579 [FJOI2018] 邮递员问题 过难
• P4588 [TJOI2018] 数学计算 AC
  用线段树维护这个操作过程，无非是两种操作：单点赋值，全局乘积。
• P4589 [TJOI2018] 智力竞赛
  求 DAG 的不可交链覆盖：拆点 + 二分图匹配。
  求 DAG 的可相交链覆盖：Floyd 传递闭包，\(u\) 能到达 \(v\) 则连边 \(u \to v\) 建新图，在这个 DAG 上求不可相交链覆盖。
  最小值的最大值……二分答案。
• P4590 [TJOI2018] 游园会 过偏（DP 套 DP）
• P4591 [TJOI2018] 碱基序列
  经典 DP 分段问题，直接 \(f_{i, j}\) 表示前 \(i\) 个字符划分出前 \(j\) 个字符串就行了。
  至于转移，可以 hash 预处理。
• P4592 [TJOI2018] 异或
  子树的查询是 naive 的，直接按照 DFS 序建一棵可持久化 \(0/1\) trie 就行了。
  链的查询则比较巧妙，我们按照从根到 \(u\) 的路径的顺序建可持久化 \(0/1\) trie（也就是 version \(u\) 的上一个版本是 version \(\textit{fa}(v)\)），查询的时候就查 \(s_u + s_v - s_{lca} - s_{\textit{fa}(lca)}\) 即可。
  经典例题是 P2633 Count on a tree，只不过这题是主席树。
• P4593 [TJOI2018] 教科书般的亵渎
  转化为求自然数幂和的问题。
  \(S(n) = \sum\limits_{i=1}^{n} i^k\) 是一个关于 \(n\) 的 \(k + 1\) 次多项式。
  拉格朗日差值法，暴力计算 \(S(1) \sim S(k+1)\) 即可，有 \(f(x) = \sum\limits_{i=1}^{c} y_i \prod\limits_{j \ne i} \frac{x - x_j}{x_i - x_j}\)。
• P4605 [SDOI2018] 物理实验 过难
• P4606 [SDOI2018] 战略游戏 过偏（圆方树）
• P4607 [SDOI2018] 反回文串 过难
• P4618 [SDOI2018] 原题识别 过偏（虽然是紫题，到现在 AC 人数还不到 \(100\)……）
• P4619 [SDOI2018] 旧试题
  关于约数个数的经典结论：\(d(xy) = \sum_{i|x} \sum_{j|y} [\gcd(i, j) = 1]\)，以及它的多元推广形式 \(d(\prod\limits_{i=1}^{n} x_i) = \sum\limits_{i_k | x_k} \prod\limits_{1 \le p < q \le n} [\gcd(i_p, i_q) = 1]\)。
  三元组计数问题可以考虑联想三元环计数，无向图的三元环计数的做法是将边由度数较小的点连向度数较大的点，复杂度是 \(O(m \sqrt{m})\)。
• P4620 [SDOI2018] 荣誉称号
  看到 \(\lfloor \frac{x}{2^{k}} \rfloor\) 可以联想到满二叉树上的 \(k\) 级祖先，于是不难发现按照 \(dep \bmod k\) 分类，这些层的先在模意义下应当是相等的，所以可以对前 \(k\) 层 DP。
  预处理代价复杂度不应和 \(n\) 有关，可以递推 “全部修改为 \(m\) 的倍数” 和 “全部修改为 \(m+1\) 的倍数” 之间的关系。