CSP-S 2022 复赛题解
退役选手口胡 /oh /oh /oh，有问题敬请指出
假期计划（holiday）
首先进行 \(n\) 次 BFS 预处理出 \(dist(i, j)\)，表示两两之间的最少中转点个数（最短路）。
直觉告诉我们应该枚举 \(B, C\)。那么 \(B-C\) 能不能 \(k\) 步到达直接利用 \(dist(B, C) \le k\) 来判断即可。接下来考虑对于已经确定的 \(B, C\)，应该如何选择合理的 \(A, D\)。
\((A, B)\) 和 \((D, C)\) 应该是完全等价的，这里不妨考虑前者。如果不考虑“点不重复”的限制，那么 \(A\) 应该是所有满足 \(dist(1, A) \le k\) 且 \(dist(A, B) \le k\) 的点中权值最大的。预处理这个最优的决策点为 \(A_1[B]\)。同理预处理出次优点、次次优点，分别记为 \(A_2[B]\)、\(A_3[B]\)。
那么，在枚举 \(B, C\) 之后，调用所有 \(9\) 组 \(A_i[B]\) 和 \(D_j[C]\)，判断合法性（是否重复）并计算权值最大的方案即可。显然这 \(9\) 种方案里必然存在一种方案是四个点互不相同的。
最短路、预处理、计算答案的时间复杂度均为 \(O(n^2)\)。
策略游戏（game）
首先分析当先手已经把 \(A_i\) 选定时，后手应该怎么选择 \(B_j\) 去使得答案最小：
- 能取异号的，那必然选异号的，而且要取绝对值最大的那个；
- 没有异号的，考虑取 \(0\)；
- 如果只能取同号的，那么一定取绝对值最小的那个。
总结一下以上几条策略，发现需要用到的量包括：区间内「负数」「正数」的“最大”和“最小”值以及「\(0\)」。在这样的情形下，考虑先手应该如何应对，不难发现，先手要取的数也必然是以上几种之一。
因此，使用线段树 / ST 表维护区间的以上几种信息。对于一次询问，先查询到 \(A[l_1, r_1]\) 和 \(B[l_2, r_2]\) 的这 5 个信息后，依次枚举先手决策、后手决策，对每个先手决策取最小值的最大值即是答案。
时间复杂度 \(O(n \log n)\)。
星战（galaxy）
先把题面要求的东西翻译成人话：有一些删边、加边操作，查询是不是每个点的出度都恰好为 \(1\)（因为如果每个点都有出度的话，必然可以永远地走下去）。
既然如此，考虑维护每个点的出度。设集合 \(S\) 表示目前存在的所有边的起点构成的可重集，那么，答案是 YES 当且仅当 \(S = \{1, 2, \cdots, n\}\)。这里只需要判断集合是否相等，可以采用维护哈希值的方法，比如维护集合内元素的一次方和、二次方和、异或和之类的，看看两边是不是相同。
问题转化为了，在题目给定的加边、删边的条件下，动态维护 \(S\) 的一些哈希值 \(H\)。对于只有单点加、删，可以直接对哈希值 \(H\) 进行修改。对于带有加、删以一个点 \(i\) 为终点的所有边的时候情形稍复杂，可以预处理 \(U_i\) 表示 \(i\) 的所有入边对应起点的哈希值（比如一次方和、二次方和、异或和），动态维护 \(C_i\) 表示当前时刻 \(i\) 存在的所有入边对应起点的哈希值，以此来辅助更新。比如 \(H\) 如果设定为一次方和，那么此时对 \(v\) 进行第四类修复即可以表示为 \(H \gets H + (U_v - C_v)\)、\(C_v \gets U_v\)。其他同理。
时间复杂度 \(O(n)\)。
数据传输（transmit）
\(k=1\) 的时候直接退化为求带权距离，再一来这是个静态问题，这启发我们使用树上倍增。
对于 \(k=2\)，考虑求 \(s, t\) 的答案的时候，把 \(s, t\) 之间的链按顺序写下来，记作 \(u_1 = s, u_2, u_3, \cdots, u_m = t\)，答案就应该是，选定其中的若干项，相邻两项之间的下标差不超过 \(2\)，然后求对应权值和的最小值。暴力做法可以是 dp，比如 \(f_{i}\) 表示最后一个当前落在 \(i\)，最小权值和，转移的时候往前枚举至多两项（\(f_{i-1}, f_{i-2}\)）来更新即可。
现在魔改这个东西变成树上倍增，用 \(f(u, p, i, j)\)（\(0 \le i, j < k\)）表示考虑从 \(u\) 开始往上 \(2^p\) 个点构成的数列，从距离 \(u\) 为 \(i\) 的点走到距离 \(2^{p}\text{-th father}(u)\) 为 \(j\) 的点的答案。初始化为 \(f(u, 0, 0, 1) = v_u\)。对每组 \((i, j)\)，转移的时候 \(O(k^2)\) 枚举跨越中线的一步是经过哪两个点来暴力合并，形式化来说就是 \(f(u, p, i, j) = \min \{ f(u, p-1, i, x) + f(2^{p-1}\text{-th father}(u), p-1, y, j) \}\)。然后类似求距离的方法，在 LCA 处也是 \(O(k^2)\) 暴力合并计算答案。
而对于 \(k=3\)，上述做法可能会出现问题，具体表现为可以“折返”：
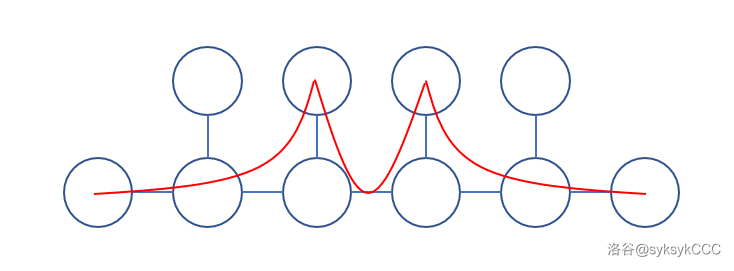
其实这个问题通过改变 \(f\) 的初始化方式就可以解决。除了初始化 \(f(u, 0, 0, 1)\) 为 \(v_u\) 之外，我们还额外地初始化 \(f(u, 0, t,t+1)\)（\(t < k\)）为距离 \(u\) 不超过 \(t\) 的点的 \(v\) 的最小值（可以通过递推实现）。回顾上述 \(k=2\) 的流程，发现所有的“折返”都被解决了。
时间复杂度 \(O(n k^4 \log n)\)，感觉有点卡？
