Codeforces 1517G Starry Night Camping

将点按照 \(x\) 坐标的奇偶性，\(y\) 坐标的奇偶性分为 \(4\) 类，可以发现如下性质：

1. 每一个不满足题意的平行四边形都包含了 \(4\) 类点恰好一个。
2. 每一个不满足题意的平行四边形都可以表示为 \(\text{(odd, odd)} \to \text{(even, odd)} \to \text{(even, even)} \to \text{(odd, even)}\) 的一条道路。

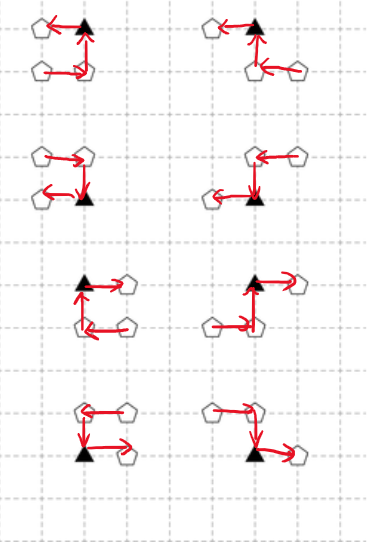
于是题目转化为，丢掉总权值最小的点，使得不存在这样的道路，这是一个最小割模型。

具体的，删点的话可以考虑拆点，将每个点 \(u\) 表示为 \(u_{in}, u_{out}\) 两个点。

根据路径经过的顺序，将上面那 \(4\) 类点分为 \(A, B, C, D\)，同时建立源点 \(S\) 和汇点 \(T\)。

图为：

• \(u_{in} \to u_{out}\) 连容量为 \(w_u\) 的边。
• \(S \to a_{in}\ (a \in A)\) 连容量为 \(+\infty\) 的边。
• \(a_{out} \to b_{in}\ (a \in A, b \in B, \text{dist}(a, b) = 1)\) 连容量为 \(+\infty\) 的边。
• \(b_{out} \to c_{in}\ (b \in B, c \in C, \text{dist}(b, c) = 1)\) 连容量为 \(+\infty\) 的边。
• \(c_{out} \to d_{in}\ (c \in C, d \in D, \text{dist}(c, d) = 1)\) 连容量为 \(+\infty\) 的边。
• \(d_{out} \to T\ (d \in D)\) 连容量为 \(+\infty\) 的边。

求最小割即可，边数和点数都是 \(O(n)\) 级别的。

#include <bits/stdc++.h>
#define int long long
#define Get(x) ((x % 2 + 2) % 2)
using namespace std;
const int N = 2005, M = 10005;
struct edge
{
	int v, w, nxt;
} e[M << 1];
int cnt = -1, n, m, s, t, maxflow, h[N], lev[N], cur[N];
inline void AddEdge(int u, int v, int w)
{
	e[++cnt] = (edge){v, w, h[u]}; h[u] = cnt;
	e[++cnt] = (edge){u, 0, h[v]}; h[v] = cnt;
}
int DFS(int u, int canflow)
{
	if(u == t) return canflow;
	int resflow = 0;
	for(int& i = cur[u]; ~i; i = e[i].nxt)
	{
		int v = e[i].v;
		if(lev[v] == lev[u] + 1 && e[i].w > 0)
		{
			int willflow = DFS(v, min(e[i].w, canflow));
			canflow -= willflow;
			resflow += willflow;
			e[i].w -= willflow;
			e[i ^ 1].w += willflow;
			if(!canflow) break;
		}
	}
	if(!resflow) lev[u] = -1;
	return resflow;
}
bool BFS()
{
	memset(lev, -1, sizeof lev);
	queue<int> que;
	que.push(t);
	lev[t] = 998244353;
	while(!que.empty())
	{
		int u = que.front(); que.pop();
		for(int i = h[u]; ~i; i = e[i].nxt)
		{
			int v = e[i].v;
			if(lev[v] != -1 || e[i ^ 1].w <= 0) continue;
			lev[v] = lev[u] - 1;
			if(v == s) return true;
			que.push(v); 
		}
	}
	return lev[s] != -1;
}
void Dinic()
{
	while(BFS())
	{
		memcpy(cur, h, sizeof h);
		maxflow += DFS(s, INT_MAX);
	}
}
int x[N], y[N], w[N], type[N], sum;
signed main()
{
	ios::sync_with_stdio(false);
	memset(h, -1, sizeof h);
	cin >> n;
	for(int i = 1; i <= n; i++) { cin >> x[i] >> y[i] >> w[i]; sum += w[i]; }
	s = 1; t = n * 2 + 2;
	for(int i = 1; i <= n; i++)
	{
		if(Get(x[i]) == 1 && Get(y[i]) == 1) type[i] = 1;
		if(Get(x[i]) == 0 && Get(y[i]) == 1) type[i] = 2;
		if(Get(x[i]) == 0 && Get(y[i]) == 0) type[i] = 3;
		if(Get(x[i]) == 1 && Get(y[i]) == 0) type[i] = 4;
	}
	for(int i = 1; i <= n; i++) AddEdge(i << 1, i << 1 | 1, w[i]);
	for(int i = 1; i <= n; i++) if(type[i] == 1) AddEdge(s, i << 1, LLONG_MAX / 64);
	for(int i = 1; i <= n; i++) if(type[i] == 1)
		for(int j = 1; j <= n; j++) if(type[j] == 2)
			if(abs(x[i] - x[j]) + abs(y[i] - y[j]) == 1)
				AddEdge(i << 1 | 1, j << 1, LLONG_MAX / 64);
	for(int i = 1; i <= n; i++) if(type[i] == 2)
		for(int j = 1; j <= n; j++) if(type[j] == 3)
			if(abs(x[i] - x[j]) + abs(y[i] - y[j]) == 1)
				AddEdge(i << 1 | 1, j << 1, LLONG_MAX / 64);
	for(int i = 1; i <= n; i++) if(type[i] == 3)
		for(int j = 1; j <= n; j++) if(type[j] == 4)
			if(abs(x[i] - x[j]) + abs(y[i] - y[j]) == 1)
				AddEdge(i << 1 | 1, j << 1, LLONG_MAX / 64);
	for(int i = 1; i <= n; i++) if(type[i] == 4) AddEdge(i << 1 | 1, t, LLONG_MAX / 64);
	Dinic();
	cout << sum - maxflow << endl;
	return 0;
}