Codeforces 1508D Swap Pass
可以发现，无论原本平面上的点是长成啥样、原本排列是长成啥样，我们都可以构造出一种方案，如下。
分析平面上的点的位置显然比分析排列要复杂得多，所以我们不妨从排列入手，做这么两件事：
1. 所有 $a_i = i$ 的点都可以被忽略掉（显然）。
2. 把 $i \to a_i$ 连边，排列会被划分为若干个置换环。
接下来可以关注到如下事实：
性质 1：对于一个环，我们可以选择一个点 $u$，不断 $\operatorname{swap}(u, a_u)$，最终所有的标签都会归位，并且这么做并不会产生任何交点。最终产生的将是一张菊花图，$u$ 是菊花图的花心。
那么，如果这整张图都只有一个环的话，题目就已经解决了。现在尝试解决多个环的情况。
性质 2：如果我们有两个不同的环，$u$ 属于第一个环中，$v$ 属于第二个环中，那么我们执行 $\operatorname{swap}(u, v)$，这两个环就会被缩为一个环。
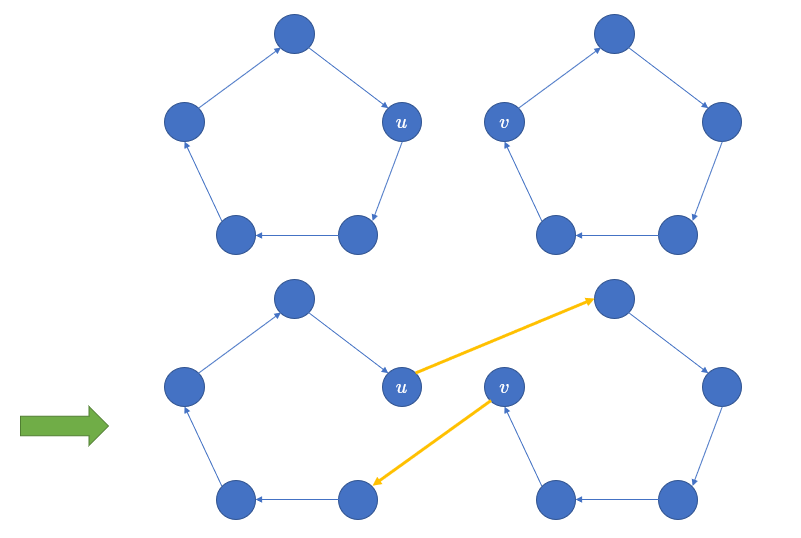
通过综合利用上面两个性质，我们可以得到一般的处理方式：
1. 首先，对于不同的环之间进行 $\text{swap}$，直到它们缩为一个环。
2. 然后，再利用性质 1 的方式，把所有的标签归位。
接下来需要处理的问题是，如何使得交换产生的边互不相交。不妨从这些点构成一个凸多边形的情况着手分析。
任意选取一个中枢点 $\text{pivot}$，现在，把其他所有点按照和中枢点的连线斜率排序，用 $\text{Border Segments}$（边界线段）表示两个相邻点之间的连线，用 $\text{Central Segments}$（中心线段）表示中枢点和其他点的连线。现在只使用边界线段来合并环，用中心线段来还原排列，这个问题就解决了。
这个做法对于非凸多边形适不适用呢？
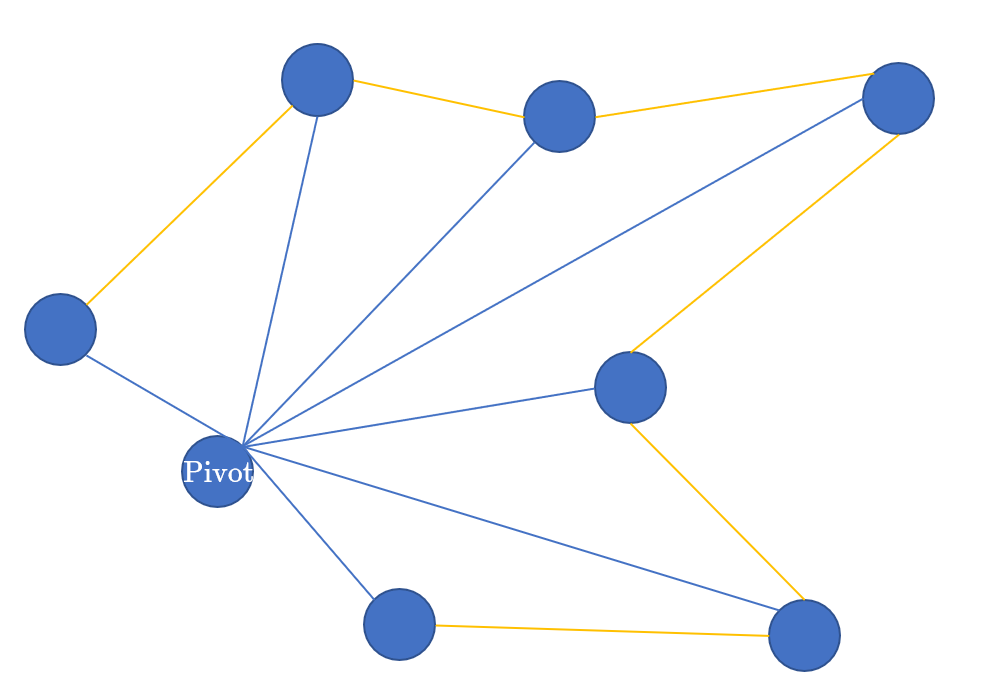
好像也可以！
但中枢点真的也可以随便选取吗？
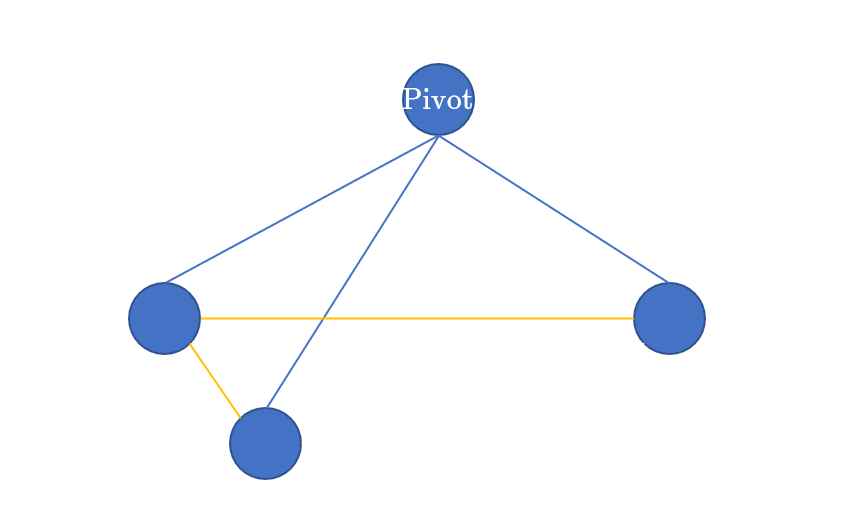
上图便是一个反例，出现边相交的原因其实是，出现了两个点的夹角大小 $>180^{\circ}$。
于是，我们钦定最左下方的那个点为中枢点即可。
在实现中，可以通过并查集维护点是否在同一个环中。因为需要极角排序，所以时间复杂度 $O(n \log n)$。
#include <bits/stdc++.h>
#define pb push_back
#define mp make_pair
#define fir first
#define sec second
using namespace std;
const int N = 2005;
int n, m, pos[N];
vector<pair<int, int>> ans;
struct disjoint_sets_union {
int fa[N];
void Init() {
for(int i = 1; i <= n; i++) {
fa[i] = i;
}
}
int Query(int p) {
if(fa[p] == p) return p;
return fa[p] = Query(fa[p]);
}
void Merge(int p, int q) {
fa[p] = q;
}
} dsu;
int pvtx, pvty, pvt;
struct point {
int x, y, a, id;
double agl;
bool operator < (const point &oth) const {
return agl < oth.agl;
}
} p[N], q[N];
int main() {
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> p[i].x >> p[i].y >> p[i].a;
p[i].id = i;
if(p[i].a != i) {
q[++m] = p[i];
}
}
if(!m) {
cout << "0\n";
return 0;
}
dsu.Init();
pvtx = q[1].x;
pvty = q[1].y;
pvt = 1;
for(int i = 2; i <= m; i++) {
if(q[i].x < pvtx) {
pvtx = q[i].x;
pvty = q[i].y;
pvt = i;
} else if(q[i].x == pvtx && q[i].y < pvty) {
pvty = q[i].y;
pvt = i;
}
}
if(pvt != 1) {
swap(q[1], q[pvt]);
}
for(int i = 2; i <= m; i++) {
q[i].agl = atan2(q[i].y - pvty, q[i].x - pvtx);
}
sort(q + 2, q + m + 1);
for(int i = 1; i <= m; i++) {
int u = dsu.Query(q[i].id);
int v = dsu.Query(q[i].a);
if(u != v) {
dsu.Merge(u, v);
}
}
for(int i = 2; i < m; i++) {
int u = dsu.Query(q[i].id);
int v = dsu.Query(q[i + 1].id);
if(u != v) {
ans.pb(mp(q[i].id, q[i + 1].id));
swap(q[i].a, q[i + 1].a);
dsu.Merge(u, v);
}
}
for(int i = 1; i <= m; i++) {
pos[q[i].id] = i;
}
while(q[1].a != q[1].id) {
int u = pos[q[1].a];
ans.pb(mp(q[1].id, q[u].id));
swap(q[1].a, q[u].a);
}
cout << ans.size() << endl;
for(unsigned i = 0; i < ans.size(); i++) {
cout << ans[i].fir << ' ' << ans[i].sec << endl;
}
return 0;
}
