Codeforces 1401E Divide Square

Description

给定一个 $10^6×10^6$ 的正方形，$n$ 条横线和 $m$ 条竖线穿过了它，求这些线把正方形分成了多少个部分。

注意: 每条线的两个端点之一一定在正方形的边上

Solution

只有两种情况，会产生一个新的块：

1. square 的对边被一条 segment 连接，如图：

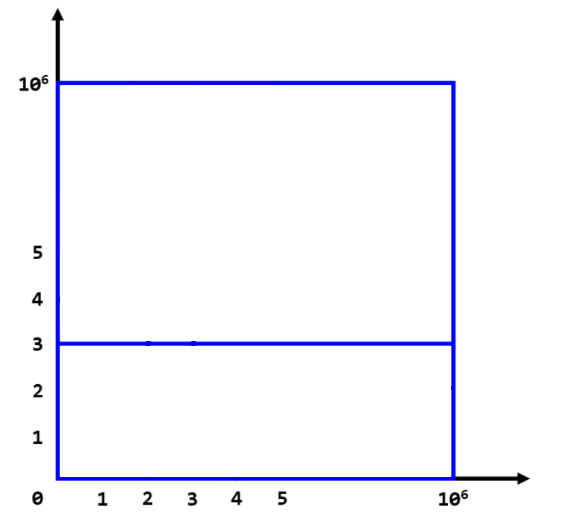
2. 两条 segment 相交，如图：

注意，因为每条 segment 必然有一段与 square 的一边相连，则两条相交必会产生一个新的块。

所以，我们可以分这两种情况来计算所有的块。

首先，$ans \gets 1$（没有 segment 也有初始的一个块）。

第一种情况是很好处理的，对于读入的某条横边或者竖边，如果它的两个端点分别为 $0$ 和 $10^6$，则 $ans \gets ans + 1$。

对于第二种情况，我们可以抽象为一个单点修改，区间查询的问题。

比如，我们把横边看作「修改」，竖边看作「查询」。

下面，我们依次处理横坐标位于 $1, 2, \cdots 10^6-1$ 的交点（也就是从左往右扫描），可以抽象为 $1-$时刻，$2-$时刻……，在每一个时刻，先处理查询操作，再处理修改操作。

尝试动态维护一个数组 $\text{cover}$，$\text{cover}_i = 0/1$ 表示在当前时刻下，纵坐标 $i$ 上面是否被线段覆盖。

• 定义操作 $\operatorname{\large{M}\small{ODIFY}}\normalsize{(t, p, v)}$ 表示在 $t$ 时刻，将 $\text{cover}_p$ 增加 $v$；
• 定义操作 $\operatorname{\large{Q}\small{UERY}}\normalsize{(t, l, r)}$ 表示询问在 $t$ 时刻，查询 $\sum\limits_{i=l}^{r}\text{cover}_i$。

描述一下一条横边 $(y, lx, rx)$，它表示，在时刻 $[lx, rx]$ 中，把 $\text{cover}_y$ 赋值为 $1$。那么，通过差分的方法，我们可以把每一条横边抽象为两个修改操作：$\operatorname{\large{M}\small{ODIFY}}\normalsize{(lx-1, y, 1)}$ 和 $\operatorname{\large{M}\small{ODIFY}}\normalsize{(rx, y, -1)}$。因为是先查询后修改，所以，$lx$ 时刻就应该被计入的贡献应该在 $lx-1$ 时刻修改，同理，$rx$ 时刻以后就要被撤销的影响应该在 $rx$ 时刻修改。

描述一下一条竖边 $(x, ly, ry)$，它会与在 $x$ 时刻，$\text{cover}_i = 1(ly \le i \le ry)$ 的那些纵坐标上的线段相交。那么，总量就是一个查询操作，即 $\operatorname{\large{Q}\small{UERY}}\normalsize{(x, ly, ry)}$，将其累加到 $ans$ 中。

那么，将所有操作按照「时间不同时，按照时间升序；时间相同时，先修改后查询」的方式排序，这就成为了一个标准的单点修改，区间查询的问题，可以用树状数组/线段树解决。

时间复杂度 $\mathcal O(n \log n)$，代码中用的是树状数组，将坐标范围平移到了 $[1, 10^6 + 1]$ 防止越界，并且将修改和查询分开了，当然也可以存在一起排序。

#include <bits/stdc++.h>
#define int long long
#define AddModification(t, p, v) mdfy[++m0] = (modification){t, p, v};
#define AddQuery(t, l, r) qry[++q0] = (query){t, l, r};
using namespace std;
const int N = 1e5 + 5, S = 1e6 + 5;
int y[N], lx[N], rx[N], x[N], ly[N], ry[N];
int ans = 1, n, m, o[S], m0, q0;
struct modification
{
	int t, p, v;
	bool operator < (const modification &oth) const { return t < oth.t; }
} mdfy[N << 1];
struct query
{
	int t, l, r;
	bool operator < (const query &oth) const { return t < oth.t; }
} qry[N << 1];
void Modify(modification &opt)
{
	for(int p = opt.p; p < S; p += p & -p)
		o[p] += opt.v;
}
int Query(query &opt)
{
	int res = 0;
	for(int p = opt.r; p; p -= p & -p)
		res += o[p];
	for(int p = opt.l - 1; p; p -= p & -p)
		res -= o[p];
	return res;
}
signed main()
{
	scanf("%lld %lld", &n, &m);
	for(int i = 1; i <= n; i++)
	{
		scanf("%lld %lld %lld", &y[i], &lx[i], &rx[i]);
		if(lx[i] == 0 && rx[i] == 1000000) ans++;
		y[i]++; lx[i]++; rx[i]++;
		AddModification(lx[i] - 1, y[i], 1);
		AddModification(rx[i], y[i], -1);
	}
	for(int i = 1; i <= m; i++)
	{
		scanf("%lld %lld %lld", &x[i], &ly[i], &ry[i]);
		if(ly[i] == 0 && ry[i] == 1000000) ans++;
		x[i]++; ly[i]++; ry[i]++;
		AddQuery(x[i], ly[i], ry[i]);
	}
	sort(mdfy + 1, mdfy + m0 + 1);
	sort(qry + 1, qry + q0 + 1);
	int nowm = 1, nowq = 1;
	for(; nowm <= m0 && mdfy[nowm].t == 0; nowm++) Modify(mdfy[nowm]);
	for(int t = 1; t < S; t++)
	{
		for(; nowq <= q0 && qry[nowq].t == t; nowq++) ans += Query(qry[nowq]);
		for(; nowm <= m0 && mdfy[nowm].t == t; nowm++) Modify(mdfy[nowm]);
	}
	printf("%lld\n", ans);
	return 0;
}