Codeforces 1364D Ehab's Last Corollary

Description

给出一张 $n$ 个点的无向连通图和一个常数 $k$。

你需要解决以下两个问题的任何一个：

1. 找出一个大小为 $\lceil\frac{k}{2}\rceil$的独立集。
2. 找出一个大小不超过 $k$ 的环。

独立集是一个点的集合，满足其中任意两点之间在原图上没有边直接相连。

$3 \le k \le n \le 10^5$，$n - 1\le m \le 2 \times 10^5$

Solution

想一想，「简单环」和「独立集」有什么关系？

如果一个大小为 $s$ 的环是不可分割的，那么，把环上的元素隔一位取一个，就可以分为两个大小为 $\lfloor\frac{s}{2}\rfloor$ 的独立集。

下图展示的是 $s = 5$ 的一种分法，分割出了 $\{1, 3\}$ 和 $\{ 2, 4\}$ 两个独立集：

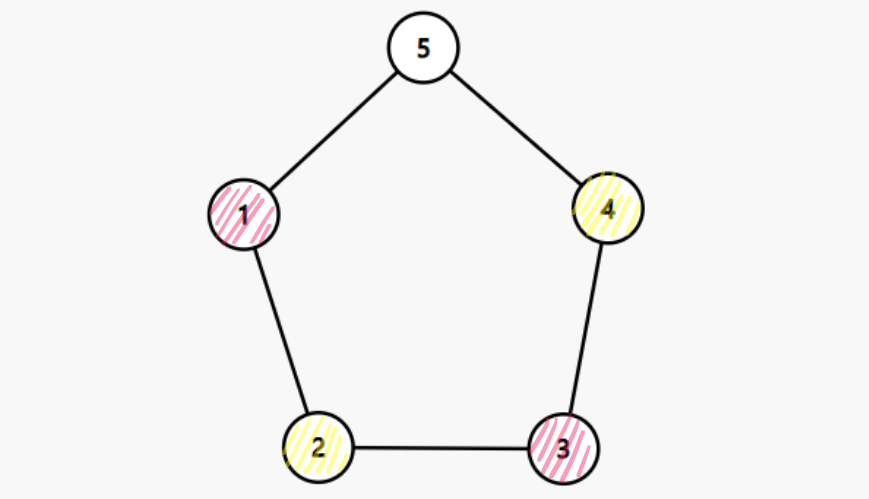
关键在于找出一个「不可分割的环」，比方说它的大小为 $a$，要是 $a \le k$，那么我们就完成任务 2 了，直接输出它就好，否则（$a > k$），必然有 $\lfloor\frac{a}{2}\rfloor \ge \lceil\frac{k}{2}\rceil$，这意味着，在这个分割出来的独立集中再分割一个大小为 $\lceil\frac{k}{2}\rceil$ 的独立集就可以完成任务 1 了。

所以，如果求出一个不可分割的环呢？

我们可以先在这个图中随便找出一个环，把点集按照顺序存在一个  deque （双端队列）里面。

然后，遍历每一条边 $\left<u, v\right>$，如果 $\left<u, v\right>$ 切割了现有的环，那么，就再割出来的两个小环中任选一个保留，$m$ 条边都割完为止。

具体的实现方法是，如果 $u, v$ 都在当前环中，且 $\left<u, v\right>$ 不是一条环上的边（可以比较 $u$ 和 $v$ 在环中的位置差是不是 $1$ 来确定），则 $\left<u, v\right>$ 必然切割当前环，如图：

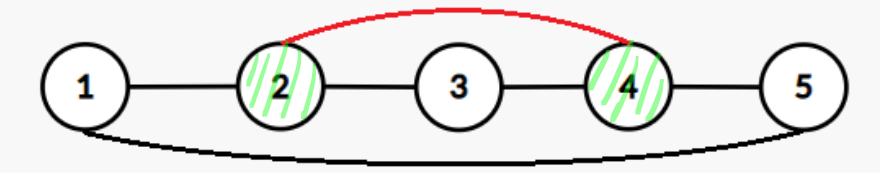
原来  deque 当中的元素依次是 $\{1, 2, 3, 4, 5\}$，现在来了条边 $\left<2, 4 \right>$ 切割，那么，必然有一个新的小环端点为 $u = 2$ 和 $v = 4$，那么把两端其余的元素弹出，就可以得到新的小环 $\{ 2, 3, 4 \}$。

当然，如果这张图一个环都没有，则这张图是树，树必然是二分图，直接二分图染色后在较大的颜色集中提取 $\lceil\frac{k}{2}\rceil$ 个来完成任务 1 就好了。

初始 DFS 找环是 $\mathcal O(n)$ 的，遍历边集是 $\mathcal O(n)$ 的，环中最多有 $n$ 个元素，所以弹出次数的总和也是 $\mathcal O(n)$ 的，所以总时间复杂度 $\mathcal O(n)$（这里不区分 $n$ 和 $m$）。

代码仅供参考：

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
vector<int> G[N];
deque<int> circ;
vector<int> s, col[2];
int n, m, k, pos[N], u[N], v[N];
bool in_circ[N];
void DFS(int u)
{
	pos[u] = s.size();
	s.push_back(u);
	col[pos[u] & 1].push_back(u);
	for(int v : G[u])
	{
		if(pos[v] == -1) DFS(v);
		else if(circ.empty() && pos[u] > pos[v] + 1)
		{
			for(int i = pos[v]; i <= pos[u]; i++)
			{
				circ.push_back(s[i]);
				in_circ[s[i]] = true;
			}
		}
	}
	s.pop_back();
}
int main()
{
	memset(pos, -1, sizeof pos);
	cin >> n >> m >> k;
	for(int i = 1; i <= m; i++)
	{
		cin >> u[i] >> v[i];
		G[u[i]].push_back(v[i]);
		G[v[i]].push_back(u[i]);
	}
	DFS(1);
	if(circ.empty())
	{
		cout << 1 << endl; 
		if(col[0].size() < col[1].size()) swap(col[0], col[1]);
		for(int i = 0; i < (k + 1) / 2; i++) cout << col[0][i] << ' ';
		return 0;
	}
	for(int i = 1; i <= m; i++)
	{
		if(in_circ[u[i]] && in_circ[v[i]] && abs(pos[u[i]] - pos[v[i]]) != 1)
		{
			while(circ.front() != u[i] && circ.front() != v[i]) 
				in_circ[circ.front()] = false, circ.pop_front();
			while(circ.back() != u[i] && circ.back() != v[i]) 
				in_circ[circ.back()] = false, circ.pop_back();
		}
	}
	if(circ.size() <= k)
	{
		cout << 2 << endl;
		cout << circ.size() << endl;
		for(int i = 0; i < circ.size(); i++) cout << circ[i] << ' ';
	}
	else
	{
		cout << 1 << endl;
		for(int i = 0; i < (k + 1) / 2; i++) cout << circ[i * 2] << ' ';
	}
	return 0;
}