Codeforces 1333E Road to 1600

Description

给一个 $n\times n$ 的棋盘，上面有 $n\times n$ 个 $[1,n\times n]$ 之间的整数且互不相同。

棋盘上有一个车和一个后，初始都在数字 $1$ 处。

走法如下：

• 车能到达同一行或同一列的任何（没有被自己访问过的）位置，后能到达同一行，同一列或同一斜线上任何（没有被自己访问过的）位置;
• 每次车和后都会走到能到达的数字中最小的。如果不存在，那么会花费 $1$ 的代价传送到整个棋盘中没有被自己访问过的数字最小的位置。

求一种方案，满足车走完的代价严格小于后走完的代价 ,或者输出 $-1$ 表示不存在这样的方案。

Solution

首先发现 $n \le 2$ 是没法做的。

然后 $n = 3$ 可以暴力算一下，比如下面这种方案就是合法的：

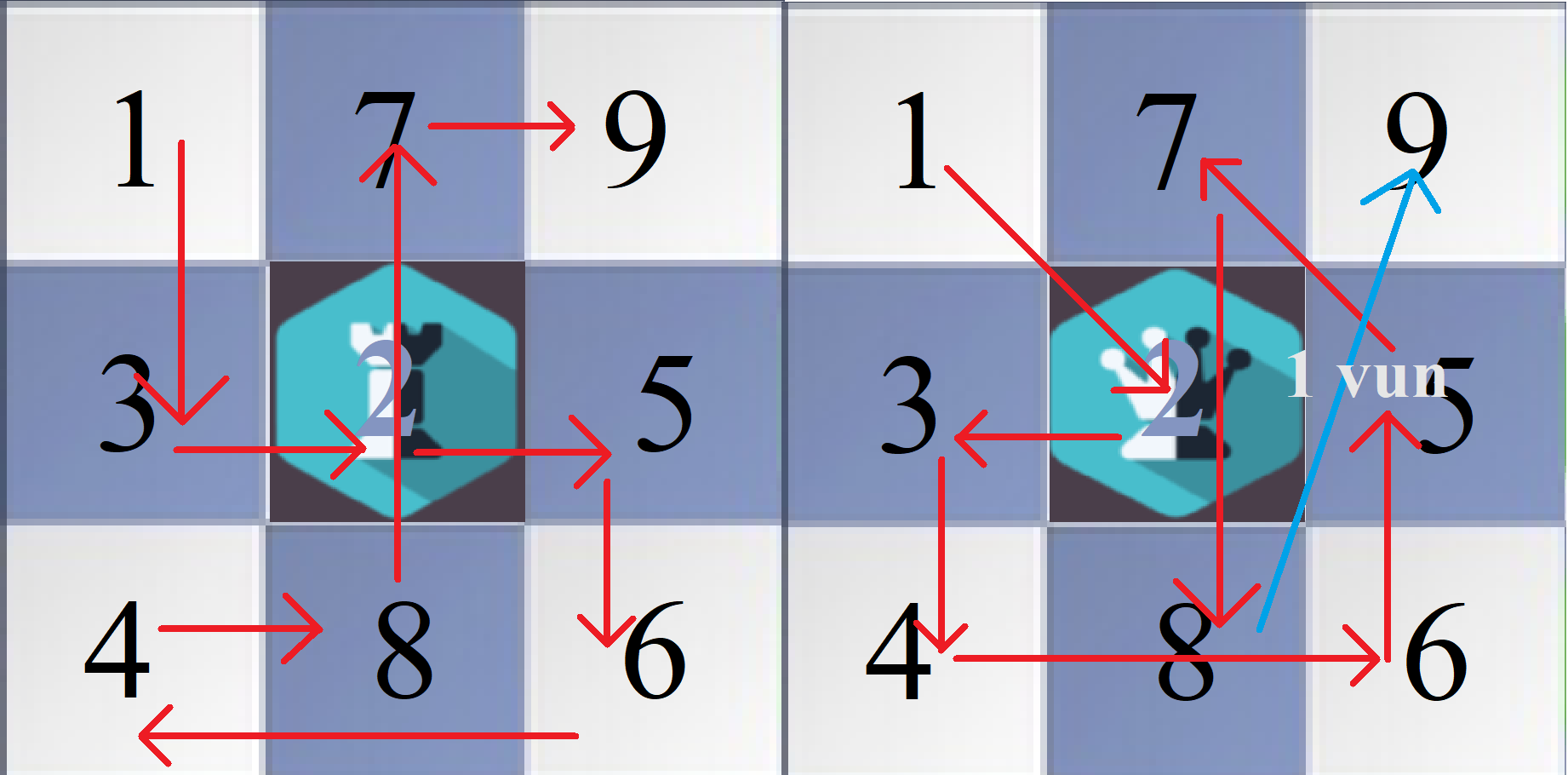
那么，如果 $n > 3$，能不能转化一下变成 $n = 3$ 的问题呢？

一种方法是使得外面的位置都不造成作用，只有最左上角的九格才发挥作用。

也就是我们只要确保两个棋子都能恰好将外面的绕完，然后进入最左上角的九宫格就行了，比如下面这样就是 $n = 5$ 的构造方法：

$$\begin{matrix} \color{red} 1 \color{blue} {+ 16} & \color{red} 7 \color{blue} {+ 16} & \color{red} 9 \color{blue} {+ 16} & 7 \to & 8 \downarrow \\ \color{red} 3 \color{blue} {+ 16} & \color{red} 2 \color{blue} {+ 16} & \color{red} 5 \color{blue} {+ 16} & 6\uparrow & 9 \downarrow \\ \color{red} 4 \color{blue} {+ 16} & \color{red} 8 \color{blue} {+ 16} & \color{red} 6 \color{blue} {+ 16} & 5\uparrow & 10 \downarrow \\ 1 \to \ & 2 \to & 3 \to & 4\uparrow & 11 \downarrow \\ 16 \gets & 15 \gets & 14 \gets & 13 \gets & 12 \gets \end{matrix}$$

于是就是一个普及组的填数问题了。

代码仅供参考。

#include <bits/stdc++.h>
using namespace std;
const int N = 505;
int n, a[N][N];
int main()
{
	scanf("%d", &n);
	if(n <= 2) return puts("-1") && 0;
	int cnt = 0, outmax = n * n - 9;
	a[1][1] = 1 + outmax; a[1][2] = 7 + outmax; a[1][3] = 9 + outmax;
	a[2][1] = 3 + outmax; a[2][2] = 2 + outmax; a[2][3] = 5 + outmax;
	a[3][1] = 4 + outmax; a[3][2] = 8 + outmax; a[3][3] = 6 + outmax;
	for(int i = 1; i <= n - 3; i++)
	{
		if(i & 1)
		{
			for(int j = 1; j <= i + 2; j++) a[i + 3][j] = ++cnt;
			a[i + 3][i + 3] = ++cnt;
			for(int j = i + 2; j >= 1; j--) a[j][i + 3] = ++cnt;
		}
		else
		{
			for(int j = 1; j <= i + 2; j++) a[j][i + 3] = ++cnt;
			a[i + 3][i + 3] = ++cnt;
			for(int j = i + 2; j >= 1; j--) a[i + 3][j] = ++cnt;
		}
	}
	for(int i = 1; i <= n; i++, puts(""))
		for(int j = 1; j <= n; j++) printf("%d ", a[i][j]); 
	return 0;
}