Codeforces 1294E Obtain a Permutation

Description

描述

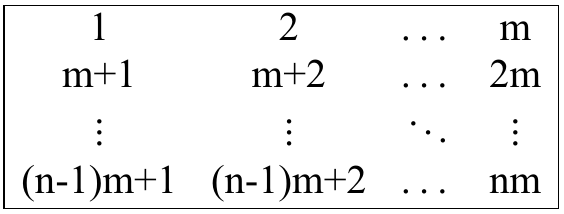
给一个 $n \times m$ 的矩阵，你想要把它还原成如下的矩阵：

你有两种操作：

• 选择一个数，修改它的值。
• 选择一列，每个元素上移一位，第一行的元素移到第 $n$ 行。

求还原的最小操作次数。

输入

第一行两个正整数 $n, m$（$1 \le n, m \le 2\times 10^5$，$n \times m \le 2 \times 10^5$）。

接下来是一个 $n \times m$ 的矩阵 $a_{i, j}$（$1 \le a_{i, j} \le 2\times 10^5$）。

输出

一个数表示答案。

样例

输入1

3 3
3 2 1
1 2 3
4 5 6

输出1

6

输入2

4 3
1 2 3
4 5 6
7 8 9
10 11 12

输出2

0

输入3

3 4
1 6 3 4
5 10 7 8
9 2 11 12

输出3

2

解释

样例1：$a_{1,1}\gets 7$，$a_{1,2} \gets 8$，$a_{1,3} \gets 9$，然后每列上移一次。

样例2：矩阵已经还原。

样例3：上移第 $2$ 列 $2$ 次。

Solution

先观察一下两种操作：

• 单点修改
• 整列上移

发现了什么？不同列之间互不影响，所以我们可以对于每一列分开处理。

那么，对于一列 $j$，因为“先修改，后上移”和“先上移，后修改”没有本质区别，所以我们定义 $same_{j, i}$（$0\le i <n$）表示将第 $j$ 列上移 $i$ 个单位后，有几个数是不用变的。那么上移了 $i$ 个单位以后，自然还有 $n - same_{j, i}$ 个数是需要变的，那么就要花费 $n - same_{j,i}$ 次修改操作，上移也花费了 $i$ 次操作，那第 $j$ 列的最优方案就是 $\min\limits_{0 \le i < n } \left(i + n - same_{j, i} \right)$，最终答案就是：

$$ans = \sum_{j = 1}^{m}\left( \min\limits_{0 \le i < n } \left(i + n - same_{j, i} \right) \right)$$

现在唯一的问题就是如何求出 $same$ 了。我们发现，如果一个数 $a_{i, j}$ 是 应该出现在第 $\boldsymbol{j}$ 列 的数字，那么一定有 $j \le a_{i,j} \le n \times m$，同时 $a_{i, j} \equiv j \pmod{m}$（后者在代码里写作了  (a[i][j] - j) % m ）。

如果上面的条件满足了，那我们就可以算一下 $a_{i,j}$ 这个数字应该出现在哪一行。显然，它应该出现在 $\dfrac{a_{i,j} - j}{m} + 1$ 行（记作 $k$）。

那如果我们把 $a_{i,j}$ 移到第 $k$ 行，它就不用变了。回顾 $same$ 的定义，从第 $i$ 行移到第 $k$ 行，要移动几次呢？

• 如果 $i \ge k$，移动 $i - k$ 个单位即可；
• 如果 $i < k$，那首先把它移到第 $1$ 行需要 $i - 1$ 次，然后再移 $1$ 次到第 $n$ 行，从第 $n$ 行移到第 $k$ 行需要 $n - k$ 次，加起来，就是 $i - 1 + 1 + n - k$，化简得 $i - k + n$。

如果合并的话，就是要移动 $(i - k + n) \bmod n$ 次，那么我们就可以把 $same_{j, (i - k + n) \bmod n}$ 增加 $1$ 了。

注意 $n, m$ 都有可能达到 $2 \times 10^5$，所以需要开不定长数组，时间复杂度 $\mathcal O(nm)$。$same$ 可以每列重复使用，舍去前一个维度。

代码贴出，仅供参考。

+ View Code?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

#include <bits/stdc++.h> using namespace std; const int NM = 2e5 + 5; int n, m, same[NM], ans; vector<int> a[NM]; int main() {     ios::sync_with_stdio(false);     cin >> n >> m;     for(int i = 1; i <= n; i++)     {         a[i].push_back(0); // 下标凑成从 1 开始         for(int j = 1; j <= m; j++)         {             int val;             cin >> val;             a[i].push_back(val);         }     }     for(int j = 1; j <= m; j++)     {         int tans = INT_MAX;         for(int i = 0; i < n; i++) same[i] = 0;         for(int i = 1; i <= n; i++)         {             if(a[i][j] < j || a[i][j] > n * m || (a[i][j] - j) % m != 0) continue;             int k = (a[i][j] - j) / m + 1;             same[(i - k + n) % n]++;         }         for(int i = 0; i < n; i++) tans = min(tans, i + n - same[i]);         ans += tans;     }     cout << ans << endl;     return 0; }