Codeforces 1292C Xenon's Attack on the Gangs
Description
描述
给一个 $n$ 个点的树,要求你将 $0 \sim n - 2$ 不重不漏的放在这 $n - 1$ 条边上,求 $S = \sum\limits_{1 \le u < v \le n} \operatorname{mex}(u, v)$ 的最大值,$\operatorname{mex}(u, v)$ 表示 $<\! u \to v \!>$ 的路径上所经过的边权集合中最小的没出现的非负数。
输入
第一行一个正整数 $n$($2 \le n \le 3000$)。
接下来 $n - 1$ 行,每行两个数 $u, v$,表示一条边($1 \le u, v \le n$,$u \neq v$)。
输出
一个数 $S$ 表示答案。
样例
输入1
3
1 2
2 3输出1
3
输入2
5
1 2
1 3
1 4
3 5输出2
10
解释
样例1:
- $\operatorname{mex}(1,2)=0$
- $\operatorname{mex}(1,3)=2$
- $\operatorname{mex}(2,3)=1$
所以 $S = 0 + 2 + 1 = 3$。
样例2:
- $\operatorname{mex}(1, 3) = 1$
- $\operatorname{mex}(1, 5) = 2$
- $\operatorname{mex}(2, 3) = 1$
- $\operatorname{mex}(2, 5) = 2$
- $\operatorname{mex}(3, 4) = 1$
- $\operatorname{mex}(4, 5) = 3$
所以 $S = 1 + 2 + 1 + 2 + 1 + 3 = 10$。
Solution
观察一下答案式子:
$$ \large
\begin{array}{rl}
S = & \!\! \sum\limits_{1\le u<v \le n} \operatorname{mex}(u, v) \\
= & \!\! \sum\limits_{x = 1}^{n} \left( \sum\limits_{\operatorname{mex}(u, v) = x} x \right) \cdots\cdots(1)\\
= & \!\! \sum\limits_{x = 1}^{n} \left( \sum\limits_{\operatorname{mex}(u, v) \ge x} 1 \right)\cdots\cdots(2)
\end{array}$$
$(1) \Rightarrow (2)$ 是怎么推的呢?
考虑一个 $\operatorname{mex}(u, v)$,比如它等于 $y$,原本它对答案只产生一次为 $y$ 的贡献;现在,它对于 $\forall 1\le x\le y$ 都会产生 $1$ 的贡献,正好和还是 $y$。
于是我们定义一个函数 $\operatorname{F}()$,$\operatorname{F}(x) = \sum_{1 \le u < v \le n}[\operatorname{mex}(u, v) \ge x]$。那么答案式子又可以化为:
$$ \large \begin{array}{rl} S = & \!\! \sum\limits_{x = 1}^{n} \left( \sum\limits_{\operatorname{mex}(u, v) \ge x} 1 \right)\cdots\cdots(2) \\
= & \!\! \sum\limits_{x = 1}^{n} \operatorname{F}(x)
\end{array} $$
$\operatorname{F}(x)$ 说通俗一点,就是 $< \! u \to v \! >$ 至少包含了 $0 \sim x - 1$ 的所有数的路径数量。
现在我们从 $0$ 开始,依次放每一个数。比如现在我们要放 $x$,$0 \sim x - 1$ 已经放好了,那么我们一定会把 $x$ 和它们放在同一条路径上,要不然 $x$ 放了以后对答案没有影响。这是因为,放在同一条路径上的话,这里的 $\operatorname{mex}$ 就要变成 $x+ 1$ 了;否则 $0 \sim x - 1$ 已经有数字缺失,那就保持那个缺失的最小数字不变。
那么我们就可以找一个 $<\!u \to v\!>$,它的长度为 $l$,我们要把 $0 \sim l - 1$ 都放在这一条路上。$l \sim n - 2$ 放的位置我们不管,因为它们不会使得答案变劣,更优的方法在后面也一定能枚举到。
想一想,一个最佳的方案一定不仅是完整的一段,而且它的一部分也要是完整的。
比如我们现在选了 $<\!u \to v\!>$:
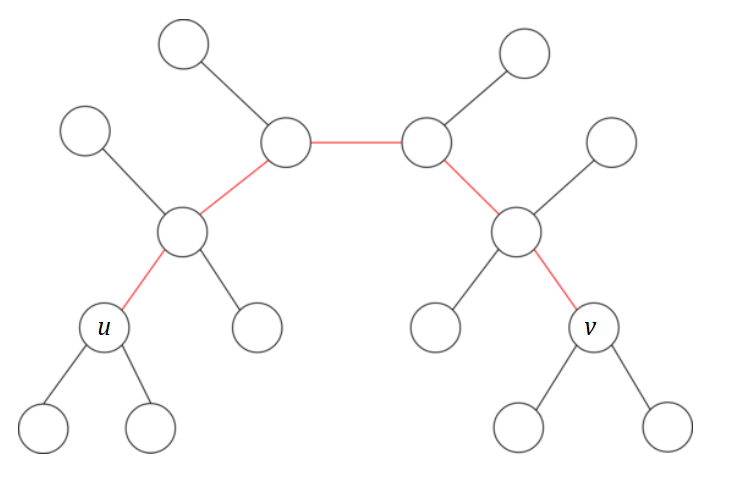
然后 $0$ 我们随便放一下:
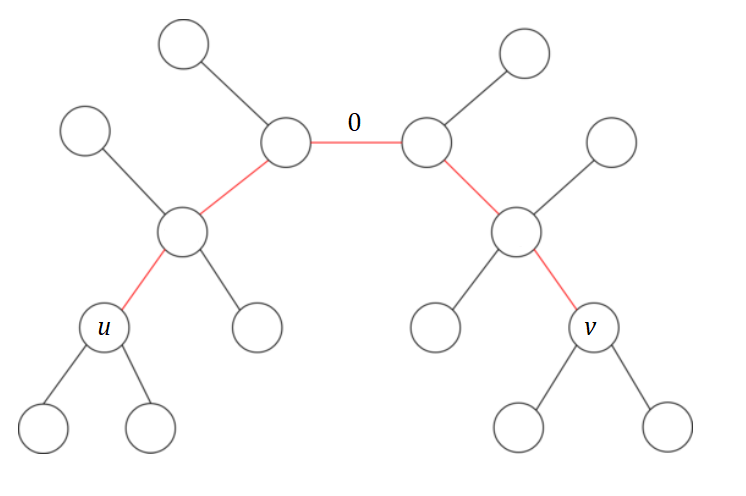
下面我们要放 $1$,为了利益最大化,显然,$1$ 和 $0$ 要在一起(这样我们在构造 $0 \sim l - 1$ 的同时也顺便构造了一个 $0 \sim 1$ 的路径)。
比如 $1$ 放在左边:
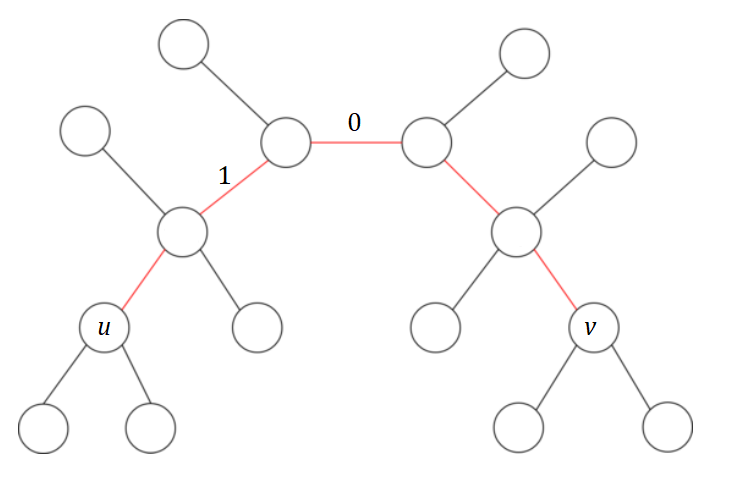
然后我们放 $2$,这时我们不管放在 $1$ 的左边还是 $0$ 的右边,都可以顺便构成 $0 \sim 2$ 的路径。
依次类推放完:
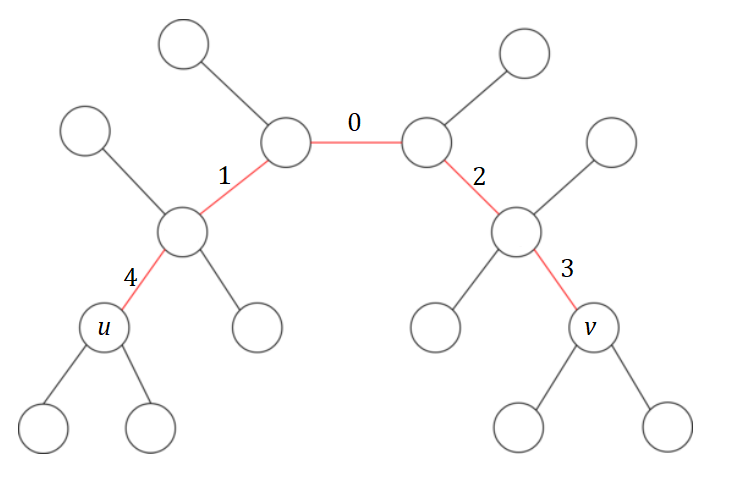
发现了什么?从 $u$ 到 $v$ 依次写下来,正好是一个 单谷序列,也就是比如把这个序列叫做 $a$,则有一个位置 $p$,使得 $a_1 > a_2 > \cdots > a_p < \cdots < a_{l-1} <a_l$。
- 用 $dp(u, v)$ 表示把 $0 \sim l - 1$ 放在 $<\!u \to v\!>$ 上,$\sum_{i =1}^{l} \operatorname{F}(i)$ 的最大可能值;
- 用 $s_{root, u}$ 表示以 $root$ 为根时,$u$ 为根的子树大小;
- 用 $p_{root, u}$ 表示以 $root$ 为根时,$u$ 的父亲。
现在我们要计算 $dp(u, v)$,根据单谷序列的性质,$l - 1$ 要么在最左边,要么在最右边,那我们分类讨论一下:
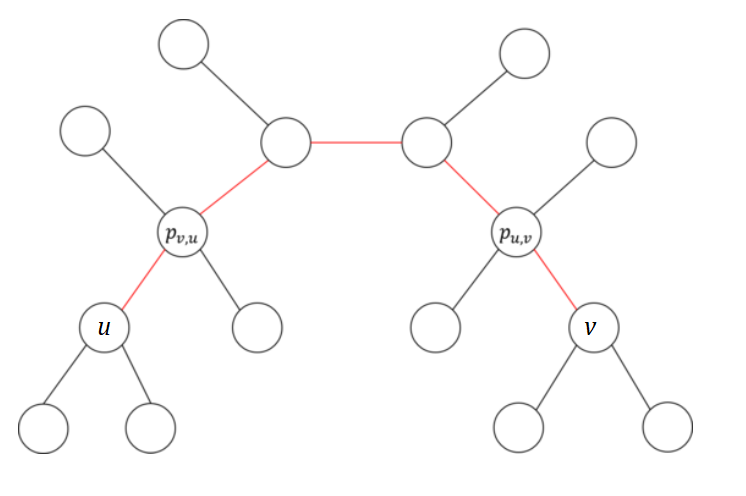
- 如果 $l - 1$ 放在最左边,那么剩下的部分就是 $dp(p_{v, u}, v)$ 的答案,而享受到 $0 \sim l - 1$ 的路径的个数就是 $\operatorname{F}(l) = s_{u, v} \times s_{v,u}$,所以 $dp(u, v) = dp(p_{v, u}, v) + s_{u, v} \times s_{v,u}$;
- 如果 $l - 1$ 放在最右边,那么剩下的部分就是 $dp(u, p_{u, v})$ 的答案,而享受到 $0 \sim l - 1$ 的路径的个数依然是 $\operatorname{F}(l) = s_{u, v} \times s_{v,u}$,所以 $dp(u, v) = dp(u, p_{u, v}) + s_{u, v} \times s_{v,u}$。
综上所述:
$$\large dp(u, v) = \max(dp(u, p_{u, v}), dp(p_{v, u}, v)) + s_{u, v} \times s_{v,u} $$
我们可以记忆化搜索,$dp(u, v)$ 就可以 $\mathcal O(1)$ 求了,总时间复杂度就是枚举 $u, v$ 的 $\mathcal O(n^2)$。至于 $p_{root, u}$ 和 $s_{root, u}$,可以在之前通过枚举 $root$,每次 $\mathcal O(n)$ 预处理出来。总时间复杂度 $\mathcal O(n^2)$。
代码贴出,仅供参考:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 3005;
int n, rt, p[N][N], s[N][N];
LL f[N][N], ans;
vector<int> G[N];
void build(int u)
{
s[rt][u] = 1;
for(int v : G[u]) if(v ^ p[rt][u])
{
p[rt][v] = u;
build(v);
s[rt][u] += s[rt][v];
}
}
LL dp(int u, int v)
{
if(u == v) return 0;
if(f[u][v]) return f[u][v];
return f[u][v] = max(dp(u, p[u][v]), dp(v, p[v][u])) + s[u][v] * s[v][u];
}
int main()
{
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1; i < n; i++)
{
int u, v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
for(int i = 1; i <= n; i++) { rt = i; build(i); }
for(int u = 1; u <= n; u++)
for(int v = 1; v <= n; v++)
ans = max(ans, dp(u, v));
cout << ans << endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号