Codeforces 1292B Aroma's Search
Description
描述
给定平面上无限个点,$\text P_0$ 的坐标为 $(x_0, y_0)$,$\text P_i$ 的坐标为 $(x_i, y_i)$,则对于任意 $i \ge 1$,有:
- $x_i = a_x \cdot x_{i - 1} + b_x$
- $y_i = a_y \cdot y_{i - 1} + b_y$
现在你在 $(x_s, y_s)$,每秒你可以上下左右移动一个单位长度,求 $t$ 秒内你最多能走到几个点。
输入
第一行六个整数 $x_0, y_0, a_x, a_y, b_x, b_y$($1 \le x_0, y_0 \le 10^{16}$,$2 \le a_x, a_y \le 100$,$0 \le b_x, b_y \le 10^{16}$)。
第二行三个正整数 $x_s, y_s, t$($1 \le x_s, y_s, t \le 10^{16}$)。
输出
一个整数表示答案。
样例
输入1
1 1 2 3 1 0
2 4 20输出1
3
输入2
1 1 2 3 1 0
15 27 26输出2
2
输入3
1 1 2 3 1 0
2 2 1输出3
0
解释
前五个点为 $(1, 1)$,$(3, 3)$,$(7, 9)$,$(15, 27)$ 和 $(31, 81)$。
样例1:收集 $(3, 3)$,$(1, 1)$,$(7, 9)$,用时 $2 + 4 + 14 = 20$ 秒。
样例2:收集 $(15, 27)$,$(7, 9)$,用时 $0 + 26 = 26$ 秒。
样例3:无法收集。
Solution
首先,很容易观察到点的一些特征:
- 都在第一象限;
- 点的分布越来越稀疏。
以样例为例:
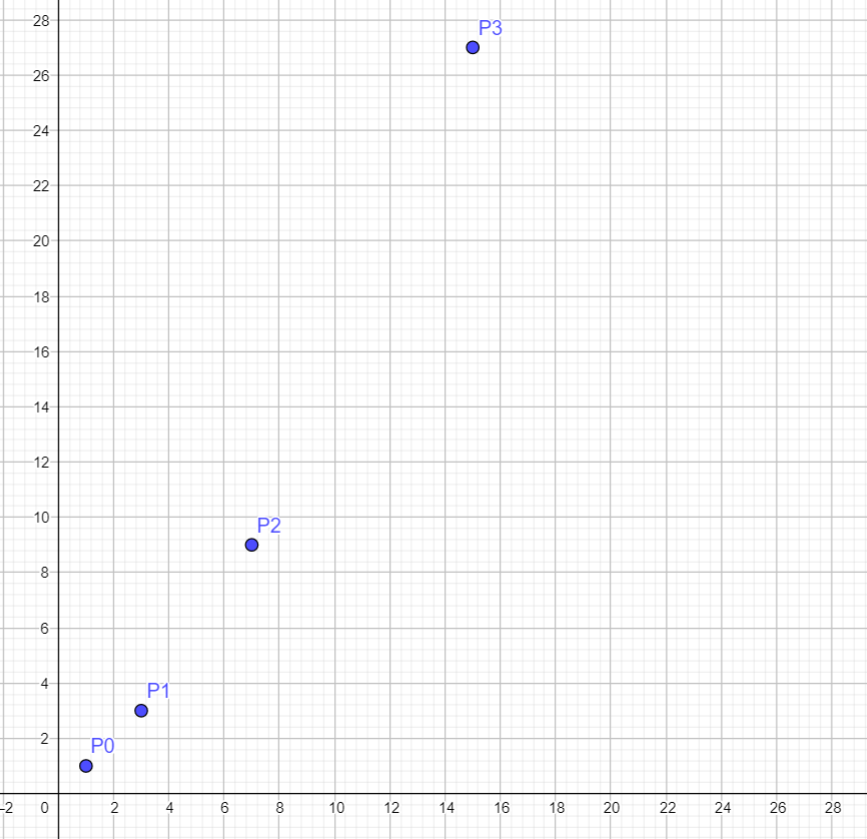
还有无限个点没有画出来。
根据点的分布越来越稀疏的特性,能不能发现收集点的规律呢?
比如我们可以先枚举一个点 $i$,直接从 $(x_s, y_s)$ 出发去收集 $\text P_i$。
然后呢?如果往 $\text P_0$ 的方向收集,点会非常密集;如果往 $\text P_\infty$ 的方向收集,点就会非常稀疏。
当然,我们往 $\text P_0$ 的方向收集!
但是,这边的点是有限的,如果全部收集完了时间还绰绰有余呢?
那就原路返回,再往 $\text P_\infty$ 的方向收集!
有人可能会疑惑,为什么这里都原路返回了,答案还是最优呢?
首先,因为随着 $j$ 的增大,$x_j, y_j$ 都在增大,所以 $\sum_{j = 1}^{i}\operatorname{dist}(\text P_{j-1}, \text P_j)$(也就是从 $\text P_i$ 收集到 $\text P_0$ 的总距离)就等于 $\operatorname{dist}(\text P_0 ,\text P_i)$($\operatorname{dist}$ 表示曼哈顿距离)。
下面为了分析方便只看 $x$ 坐标($\operatorname{Xdist}$ 表示 $x$ 坐标之差)。
点最密集的时候应该是什么时候?很显然,$a_x$ 和 $b_x$ 都最小的时候,也就是 $a_x = 2, b_x = 0$。
$$ \operatorname{Xdist}(\text P_{i+1}, \text P_{i}) = (a_x \cdot x_{i} + b_x) - x_{i} = (a_x - 1)\cdot x_{i} + b_x = x_i $$
$$ \operatorname{Xdist}(\text P_{0}, \text P_{i}) = x_i - x_0 $$
$\because x_0 \ge 1 \qquad \therefore \operatorname{Xdist}(\text P_{i+1}, \text P_{i}) > \operatorname{Xdist}(\text P_{0}, \text P_{i})$
现在 $y$ 坐标也加进来,就可以得到 $\operatorname{dist}(\text P_{i+1}, \text P_{i}) > \operatorname{dist}(\text P_{0}, \text P_{i})$。
这说明什么?收集 $\text P_0 \sim \text P_{i - 1}$ 的时间比只收集一个 $\text P_{i + 1}$ 的时间还要少!
如果当初选择向右走,那再去收集 $\text P_{i + 2}$ 的时候,显然 $\operatorname{dist}(\text P_{i+1}, \text P_{i +2}) > \operatorname{dist}(\text P_{i}, \text P_{i+1})$,那么 $\operatorname{dist}(\text P_{i+1}, \text P_{i +2}) + \operatorname{dist}(\text P_{i}, \text P_{i+1}) > 2 \operatorname{dist}(\text P_{0}, \text P_{i})$。说明向 $\text P_{\infty}$ 方向收集 $2$ 个点的时候,$\text P_0$ 方向已经回来了,并收集了 $i$ 个点,如果 $i \ge 2$ 那么直接可以知道答案更优了,还剩两种情况:
- $i=0$,这时没什么左右之分,那不影响答案;
- $i=1$,直接带入算一算,$x_1 = 2 x_0$,$x_2 = 4 x_0$,那么左边加上返回的时间是 $2 x_0$,直接去 $\text P_2$ 的时间也是 $2 x_0$,因为越往后点越稀疏,而两种方案当前耗时相同,起点不同,所以 $\text P_0$ 方向还是更优。
还有一个小问题,就是数组开多大,因为 $2^{64} > 10^{18}$,所以数组开到 $70$ 就绰绰有余了。
时间复杂度 $\mathcal O(n^2)$,$n$ 是要用到的点数,算到 $x_n > x_s, y_n > y_s, \operatorname{dist}(\text P_n, \text S) > t$ 即可。
#include <bits/stdc++.h>
#define max(a, b) a > b ? a : b
typedef long long LL;
const int N = 70;
LL ax, ay, bx, by, ans, n;
LL x[N], y[N], xs, ys, t;
LL dist(LL x1, LL y1, LL x2, LL y2) { return llabs(x1 - x2) + llabs(y1 - y2); }
int main()
{
scanf("%lld %lld %lld %lld %lld %lld", x, y, &ax, &ay, &bx, &by);
scanf("%lld %lld %lld", &xs, &ys, &t);
while(++n)
{
x[n] = ax * x[n - 1] + bx; y[n] = ay * y[n - 1] + by;
if(x[n] > xs && y[n] > ys && dist(xs, ys, x[n], y[n]) > t) break;
}
for(int i = 0; i <= n; i++)
{
LL tans = 0, tt = t;
if(dist(xs, ys, x[i], y[i]) <= tt) tt -= dist(xs, ys, x[i], y[i]), tans++; // S -> Pi
else { ans = max(ans, tans); continue; }
for(int j = i; j; j--) // Pi -> P0
{
if(dist(x[j], y[j], x[j - 1], y[j - 1]) <= tt)
tt -= dist(x[j], y[j], x[j - 1], y[j - 1]), tans++;
else break;
}
for(int j = 1; j <= n; j++) // P0 -> Pi -> P∞
{
if(dist(x[j], y[j], x[j - 1], y[j - 1]) <= tt)
tt -= dist(x[j], y[j], x[j - 1], y[j - 1]), tans += j > i; // 注意 j > i 的时候才能算入
else break;
}
ans = max(ans, tans);
}
printf("%lld\n", ans);
return 0;
}





