Codeforces 1285E Delete a Segment
Description
描述
给一个数轴上的 $n$ 条线段,第 $i$ 条覆盖了 $[l_i, r_i]$(如果 $l_i = r_i$ 的话就是一个点)。一个线段集的 并集 是一个与原线段集所覆盖点一样的线段集,例如 $n = 5$,$5$ 条线段分别为 $[1,2]$,$[2,3]$,$[4,5]$,$[4,6]$,$[6,6]$,那么它们的 并集 就是 $[1,3]$ 和 $[4,6]$ 两条线段。现在,你要求出 正好删去一条线段后,并集 最多包括多少条线段。
如果两条线段重合,你依然只能删去一条。
输入
第一行是一个正整数 $t(1 \le t \le 10^4)$,表示数据组数。
每组数据的第一行是一个正整数 $n(2 \le n \le 2 \cdot 10^5, \sum n \le 2 \cdot 10^5)$,接下来 $n$ 行每行两个整数 $l_i, r_i(-10^9 \le l_i, r_i \le 10^9)$,含义如描述所示。
输出
对于每组数据输出一个数,表示 正好删去一条线段后,并集 最多包括多少条线段。
样例
输入
3
4
1 4
2 3
3 6
5 7
3
5 5
5 5
5 5
6
3 3
1 1
5 5
1 5
2 2
4 4输出
2
1
5解释
样例解释:
- 删去 $[1,4]$,剩下 $[2,3]$,$[3,6]$,$[5,7]$,并集 大小为 $1$;
- 删去 $[2, 3]$,剩下 $[1, 4]$,$[3,6]$,$[5,7]$,并集 大小为 $1$;
- 删去 $[3, 6]$,剩下 $[1, 4]$,$[2, 3]$,$[5,7]$,并集 大小为 $2$;
- 删去 $[5, 7]$,剩下 $[1, 4]$,$[2, 3]$,$[3, 6]$,并集 大小为 $1$。
故输出为 $2$。
Solution
看到负数,首先考虑 离散化,然后就很自然地想到用 $d_i$ 来表示坐标(离散化后)为 $i$ 的点被几条线段覆盖,然后姑且不说删去一条线段,就是原线段集的 并集 怎么求呢?
画个图看看(图中为了防止线段重叠将线段进行了竖直平移,一条线段的实际覆盖区域即为其竖直投影):
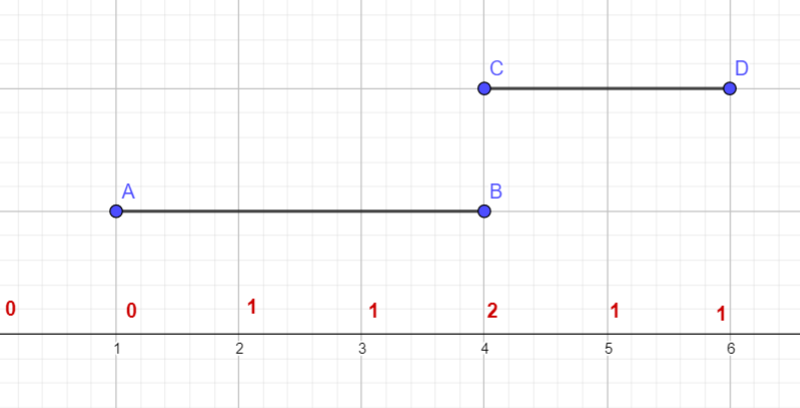
简单!连续非零段的个数就是 并集 大小!
真的是这样吗?

似乎……不太对?
于是就有了一种神仙的方法:既然我们的标号都在点上,第二张图不能很好处理,那么,我们给边也来个 $d$!
怎么实现呢?只要把所有的 $l_i, r_i$ 都 $\times 2$ 即可!
于是我们就能很好地处理了:
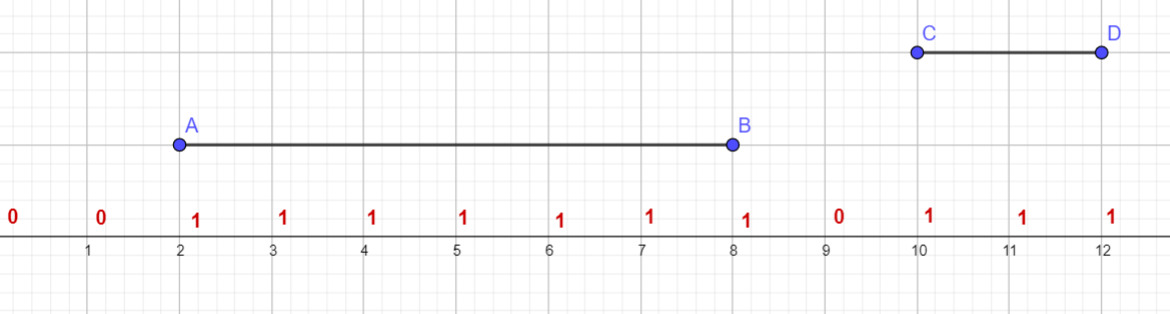
那么 $\mathcal O(n^2)$ 的做法就呼之欲出了:删去线段 $i$ 时,就把 $[l_i, r_i]$ 的 $d$ 都减去 $1$,然后重新统计一遍求最大值!
显然是过不了的,还需要优化。
把 $[l_i, r_i]$ 的 $d$ 都减去 $1$ 后,有能力成为新的空段的条件,显然是 $d = 1$,我们不妨大胆的假设一下,$[l_i, r_i]$ 中 $d = 1$ 的连续段数(显然这里的 $d$ 不会为 $0$,至少有线段 $i$ 覆盖呢),就是删去线段 $i$ 后 新增的段数。
试一下?
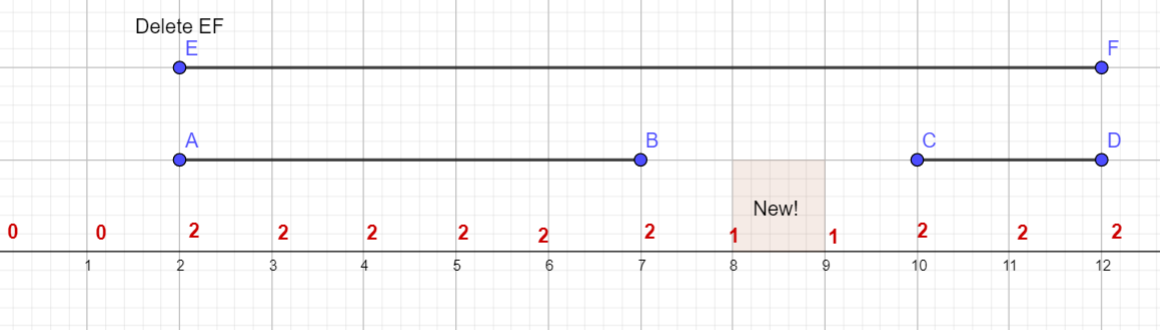
好像是对的?
那要是这样呢?
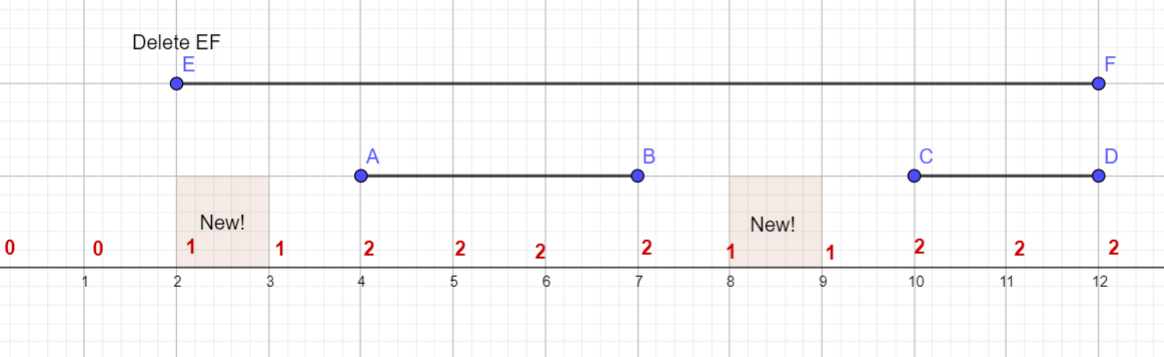
可是显然答案是增加 $1$,而不是增加 $2$ 呀?
再举个最简单的例子:
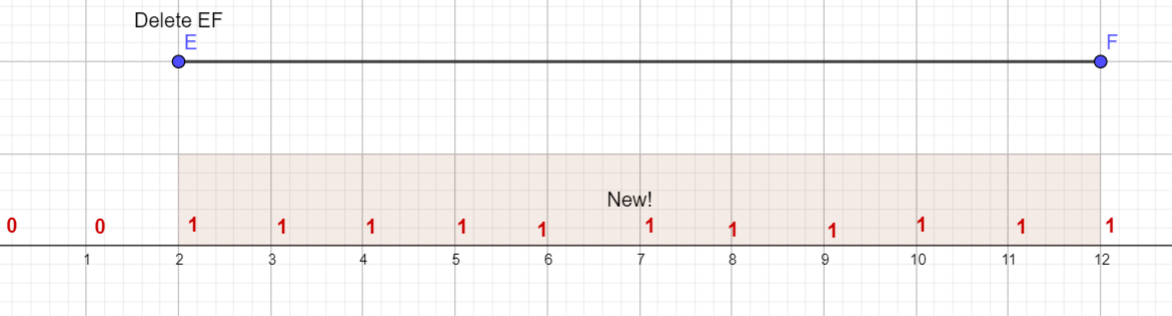
这时,显然答案是减去 $1$ 了,而不是离谱地增加 $1$。(虽然 $n \ge 2$,但这里姑且认为那个 $l$ 和 $r$ 非常大)
发现了什么?当新增段和 $l_i$ 相通时,答案要 $-1$,和 $r_i$ 相通时也要 $-1$,实现上只要判断一下 $d_{l_i}$ 和 $d_{r_i}$ 是不是等于 $1$ 就好了。
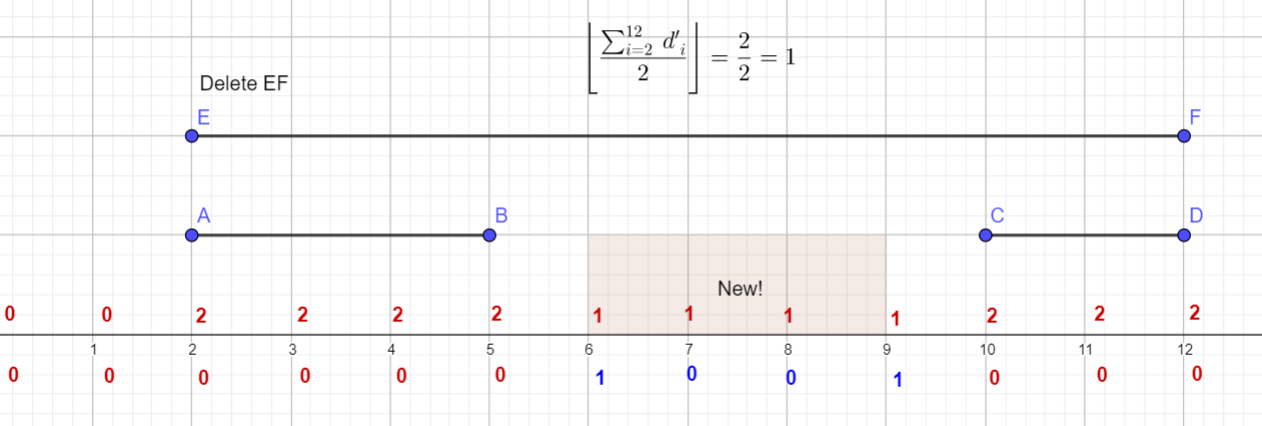
然后怎么求新增段呢?很简单,把每一个连续 $1$ 段的最左边的 $d' + 1$,最右边的 $d' + 1$,我们就可以用 $\left \lfloor \dfrac{\sum_{i = l}^{r} d'_i}{2} \right \rfloor $ 来计算段数了(想一想,为什么?),如果加上前缀和优化,那么去掉 $\mathcal O(n \log n)$ 的离散化,代码就是 $\mathcal O(n)$ 的了。
下面是一个直观的演示:
代码贴出,仅供参考。(代码中用 d_ 来表示 $d'$)
#include <bits/stdc++.h>
#define REP(i, x, y) for(register int i = x; i <= y; i++)
using namespace std;
typedef long long LL;
const int N = 2e5 + 5;
struct segment { LL l, r; } s[N];
int n;
LL ans0, ans1, tmp[N << 1], d_[N << 2], d[N << 2];
int main()
{
ios::sync_with_stdio(false);
int T;
cin >> T;
while(T--)
{
ans0 = 0; ans1 = INT_MIN;
cin >> n;
REP(i, 1, n)
{
cin >> s[i].l >> s[i].r;
tmp[(i << 1) - 1] = s[i].l;
tmp[i << 1] = s[i].r;
}
sort(tmp + 1, tmp + (n << 1) + 1);
int tot = unique(tmp + 1, tmp + (n << 1) + 1) - tmp - 1;
REP(i, 1, n)
{
s[i].l = lower_bound(tmp + 1, tmp + tot + 1, s[i].l) - tmp;
s[i].r = lower_bound(tmp + 1, tmp + tot + 1, s[i].r) - tmp;
s[i].l <<= 1LL; s[i].r <<= 1LL;
d[s[i].l]++; d[s[i].r + 1]--; // 差分算原始数组
}
tot <<= 1LL;
REP(i, 1, tot + 5) d[i] += d[i - 1];
REP(i, 0, tot + 5) ans0 += d[i] && !d[i + 1];
REP(i, 0, tot + 4) if(d[i] == 1 && d[i + 1] != 1) d_[i]++;
REP(i, 1, tot + 5) if(d[i] == 1 && d[i - 1] != 1) d_[i]++;
REP(i, 1, tot + 5) d_[i] += d_[i - 1]; // d_[] 上前缀和
REP(i, 1, n)
{
LL t = (d_[s[i].r] - d_[s[i].l - 1]) / 2;
t -= (d[s[i].r] == 1) + (d[s[i].l] == 1);
ans1 = max(ans1, t);
}
cout << ans0 + ans1 << endl; // 初始答案加上新增答案
REP(i, 0, tot + 10) d[i] = d_[i] = 0; // 用多少清多少,避免 memset 浪费时间
}
return 0;
}


