李宏毅2021春机器学习课程笔记——自注意力机制（Self-Attention）

本文作为自己学习李宏毅老师2021春机器学习课程所做笔记，记录自己身为入门阶段小白的学习理解，如果错漏、建议，还请各位博友不吝指教，感谢！！

全连接网络的输入是一个向量，但是当输入是一个变长的向量序列时，就不能再使用全连接网络了。这种情况通常可以使用卷积网络或循环网络进行编码来得到一个相同长度的输出向量序列。

基于卷积或循环网络的序列编码都是一种局部的编码方式，只建模了输入信息的局部依赖关系。虽然循环网络理论上可以建立长距离依赖关系，但是由于信息传递的容量以及梯度消失问题，实际上也只能建立短距离依赖关系。

要建立输入序列之间的长距离依赖关系，可以通过如下两种方法：

  1. 增加网络的层数，通过一个深层网络来获取远距离的信息交互；
  2. 使用全连接网络。

全连接网络是一种非常直接的建模远距离依赖的模型，但是如上边所说无法处理变长的输入序列。不同的输入长度（此处指的是向量序列的长度），其连接权重的大小也是不同的。这种情况我们就可以利用注意力机制来“动态”地生成不同连接地权重，即自注意力模型（Self-Attention Model）。

输入/输出

  1. 自注意力模型输入：如下图所示，左侧的变长的输入序列即是自注意力模型的输入数据，注意这个向量序列的长度不是固定的。
  1. 自注意力模型输出：自注意力模型的输出有三种情况：
  • 输出序列长度和输入序列长度一样，这种情况下，输入序列中的向量和结果序列中的元素一一对应，也就是为每一个输入序列中的向量给出一个label。如下图所示：
  • 输出序列的长度为1,此时相当于一个分类人物，比如像对正面/负面评论的分析。如下图所示：
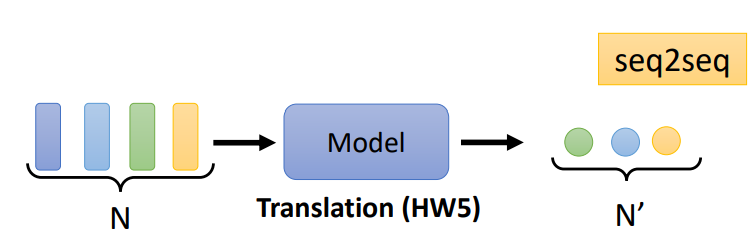
  • 输出序列的长度是不定的，这种情况其实也就是Seq2Seq模型，比如机器翻译。如下图所示：

Attention函数

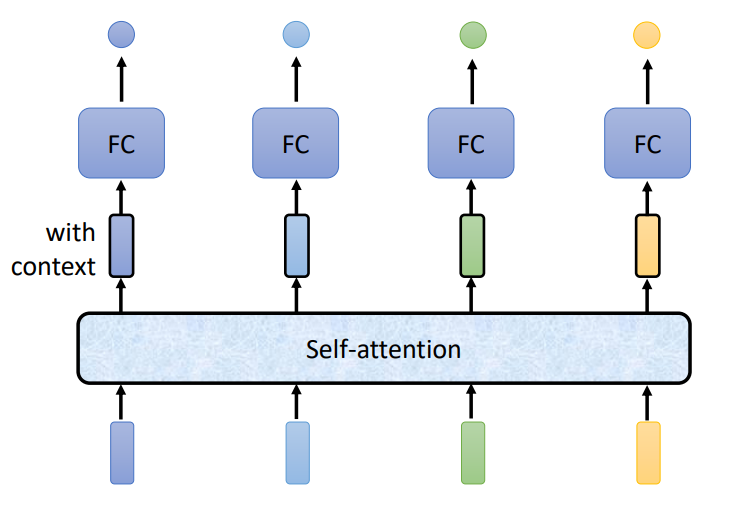
因为要建立输入向量序列的长依赖关系，所以模型要考虑整个向量序列的信息。如下图所示，Self-Attention的输出序列长度是和输入序列的长度一样的，对应的输出向量考虑了整个输入序列的信息。然后将输出向量输入到Fully-Connected网络中，做后续处理。

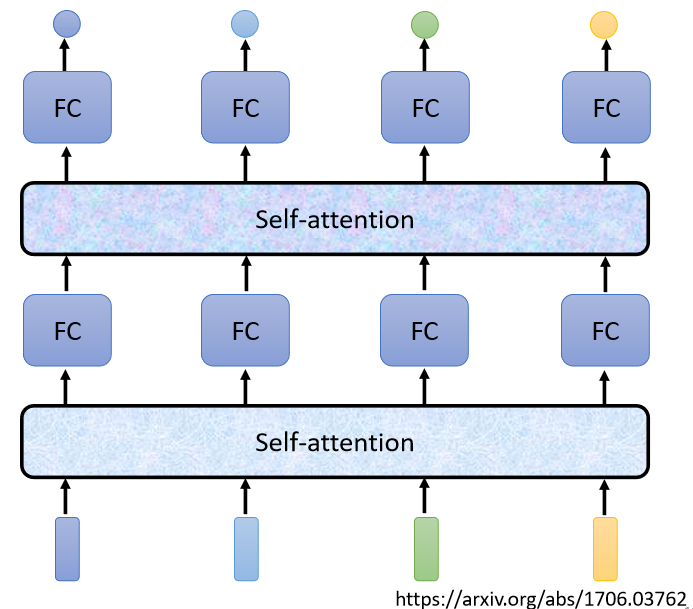
当然Self-Attention可以和Fully-Connected交替使用多次以提高网络的性能，如下图所示。

上边我们提到，Self-Attention可以使用多次，那么输入可能是整个网络的输入，也可能是前一个隐藏层的输出，这里我们使用\([a^1, a^2, a^3, a^4]\)来表示输入，使用\(b^1\)表示输出为例。

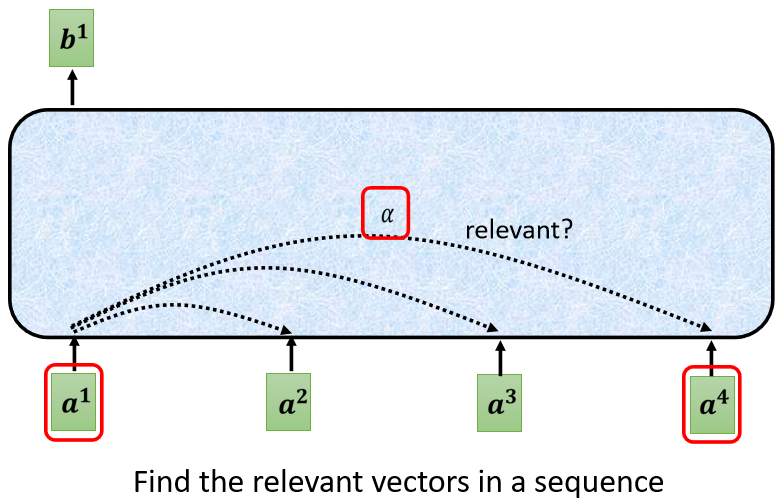
首先Self-Attention会计算\(a^1\)分别与\([a^1, a^2, a^3, a^4]\)的相关性\([\alpha_{1,1}, \alpha_{1,2}, \alpha_{1,3}, \alpha_{1,4}]\)。相关性表示了输入\([a^1, a^2, a^3, a^4]\)对\(a^1\)是哪一个label的影响大小。而相关性\(\alpha\)的计算方式共有Dot-product和Additive两种。

Dot-product

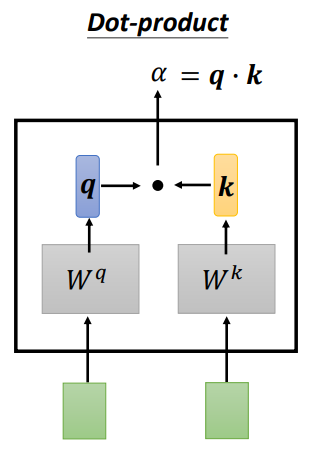
在Dot-product中，输入的两个向量，左边的向量乘上矩阵\(W^q\)得到矩阵\(q\)，右边的向量乘上矩阵\(W^k\)得到矩阵\(k\)，然后将矩阵\(q\)和矩阵\(k\)对应元素相乘并求和得到相关性\(\alpha\)。

Additive

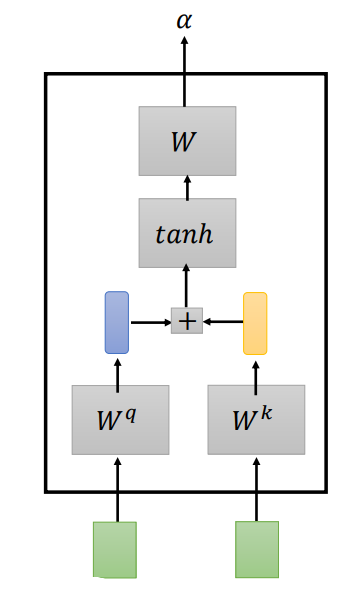
在Additive中同样也是先将两个输入向量与矩阵\(W^q\)和矩阵\(W^k\)相乘得到矩阵\(q\)和\(k\)。然后将矩阵\(q\)和\(k\)串起来输入到一个激活函数（tanh）中，在经过Transform得到相关性\(\alpha\)。

Self-Attention计算过程

为了提高模型能力，自注意力模型经常采用查询-键-值（Query-Key-Value，QKV）模型，其计算过程如下所示：

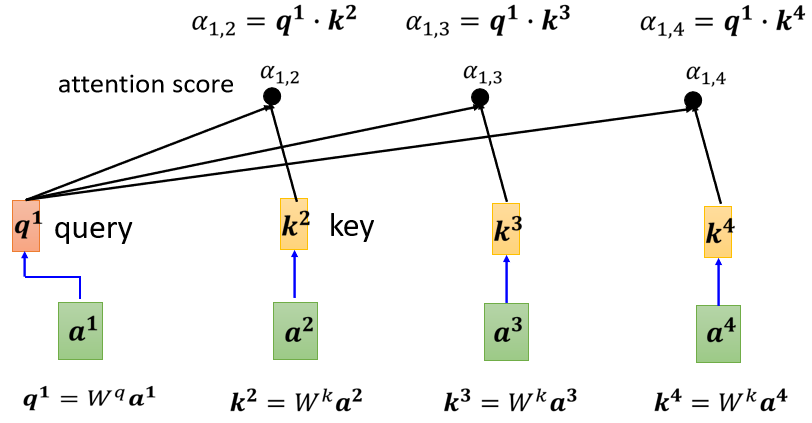
  1. 首先计算\(a^1\)与\([a^2, a^3, a^4]\)的关联性\(\alpha\)（实践时一般也会计算与\(a^1\)自己的相关性）。以Dot-product为例，我们分别将\([a^1, a^2]\),\([a^1, a^3]\),\([a^1, a^4]\)作为Dot-product的输入，求得对应的相关性\([\alpha_{1,2}, \alpha_{1,3}, \alpha_{1,4}]\)，如下图所示：
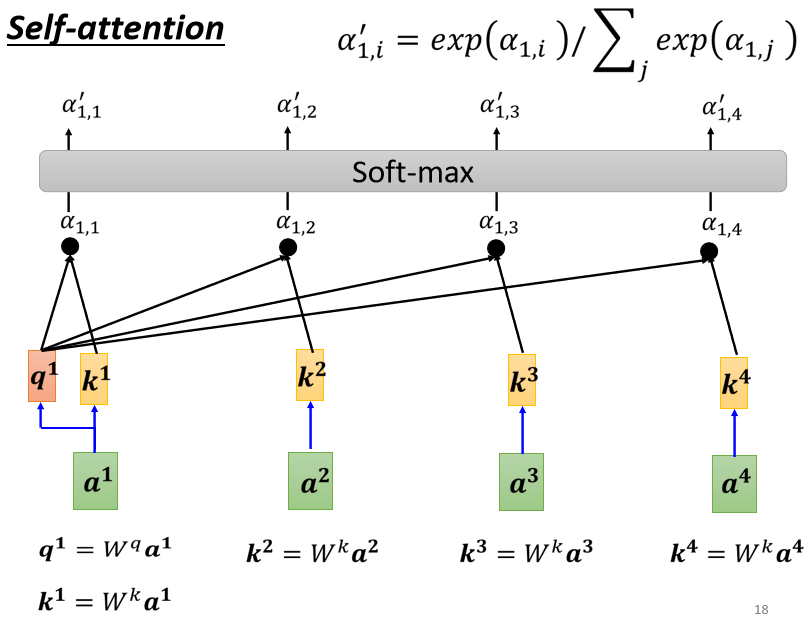
  1. 计算出\(a^1\)跟每一个向量的关联性之后，将得到的关联性输入的softmax中，这个softmax和分类使用的softmax时一样的，得到对应数量的\(\alpha'\)。（当然这里使用ReLU或其他激活函数代替softmax也是可以的，根据实际效果来）
  1. 先将\([a^1, a^2, a^3, a^4]\)每一个向量分别乘上矩阵\(W^v\)得到新的向量\(v^1, v^2, v^3, v^4\)，然后把\(v^1, v^2, v^3, v^4\)都乘上Attention的分数\(\alpha'\)，然后相加得到\(b^1 = \sum_{i} \alpha'_{1, i}v^i\)

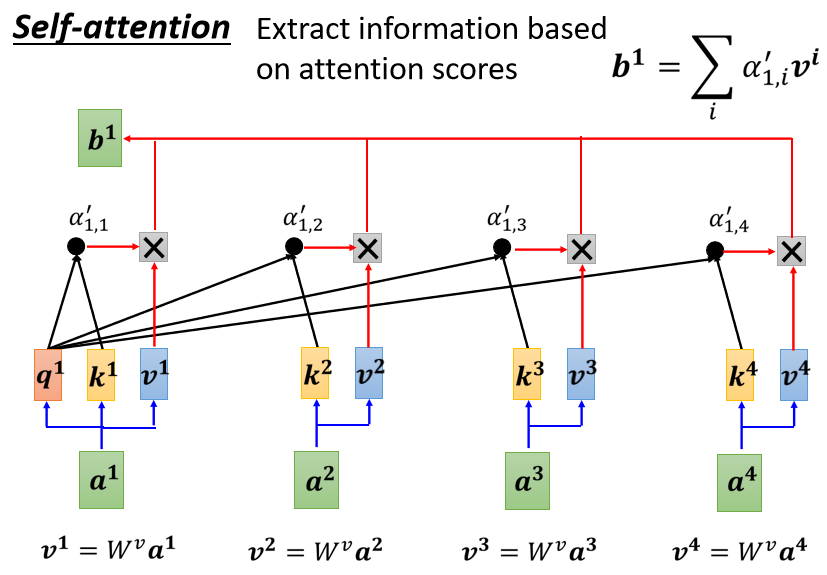
假设\(a^1\)和\(a^2\)的关联性很强，则由这两个向量计算得到的\(\alpha'_{1,2}\)的值就很大，最后求得的\(b^1\)的值，就可能会比较接近\(v^2\)。所以哪一个向量的Attention的分数最大，那一个向量的\(v\)就会主导最后计算出来的结果\(b\)。

Self-Attention计算矩阵

由上边计算过程可知，每个输入\(a\)都会产生\(q\)、\(k\)和\(v\)三个矩阵。这里还是以\([a^1, a^2, a^3, a^4]\)为输入为例：

  1. 我们将\([a^1, a^2, a^3, a^4]\)按照公式\(q^i = W^q a^i\)依次乘以矩阵\(W^q\)得到\([q^1, q^2, q^3, q^4]\)，那我们将\([a^1, a^2, a^3, a^4]\)作为4列拼成一个矩阵\(I\)，将\([q^1, q^2, q^3, q^4]\)作为4列拼成一个矩阵\(Q\)得到计算矩阵如下：（矩阵\(k\)和\(v\)的计算方式一样）
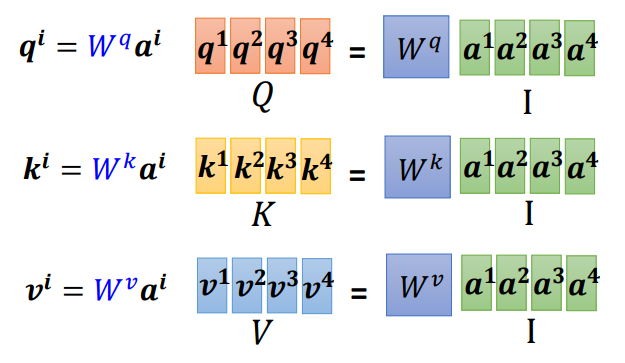
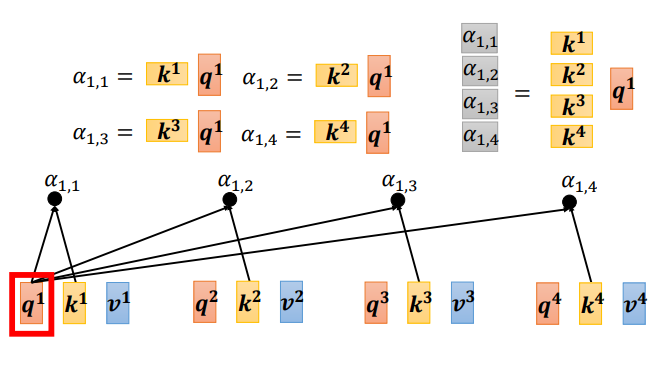
  1. 我们得到\(Q\)、\(K\)和\(V\)三个矩阵之后，下一步就是由矩阵\(Q\)和\(K\)计算关联性\(\alpha\)，先以计算\(q^1\)的关联性为例，将矩阵\(q^1\)分别与矩阵\([k^1, k^2, k^3, k^4]\)相乘得到\([\alpha_{1,1}, \alpha_{1,2}, \alpha_{1,3}, \alpha_{1, 4}]\)(我们现在是看作矩阵运算，为了方便计算，我们先对矩阵\(k^i\)进行转置，在和矩阵\(q^1\)相乘)：
  1. 我们将第一步中得到的矩阵\(K\)整体转置，与矩阵\(Q\)相乘，得到所有的相关性矩阵\(A\)；然后对attention分数（相关性）做normalization，即每次对\(A\)中的一列（每列对应着一个\(q^i\)）做softmax(也可以是其他激活函数)，让每一列的值相加为1，得到矩阵\(A'\)，如下图所示：
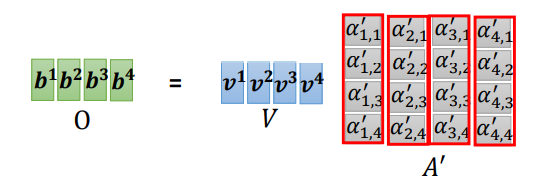
  1. 我们将矩阵\(V\)依次乘以矩阵\(A'\)中的每一列得到输出\([b^1, b^2, b^3, b^4]\)，如下图所示：

综上所述，矩阵计算公式如下：

  1. 计算\(Q\)、\(K\)和\(V\)三个矩阵

\[\begin{aligned} & Q = W^qI \\ & K = W^kI \\ & V = W^vI \\ \end{aligned} \]

  1. 计算相关性并使用softmax作normalization：

\[\begin{aligned} & A = K^TQ \\ & A' = softmax \left(A \right) \end{aligned} \]

  1. 计算最后的输出

\[O = VA' \]

通过上述计算过程，我们可以看出只有\(W^q\)、\(W^k\)和\(W^v\)三个矩阵是未知的，需要我们通过训练资料将他们学习出来。

Multi-head Self-Attention

Self-Attention有一个使用非常广泛的的进阶版Multi-head Self-Attention，具体使用多少个head，是一个需要我们自己调节的超参数（hyper parameter）。

在Self-Attention中，我们是使用\(q\)去寻找与之相关的\(k\)，但是这个相关性并不一定有一种。那多种相关性体现到计算方式上就是有多个矩阵\(q\)，不同的\(q\)负责代表不同的相关性。我们以2 heads为例，先使用\(a\)计算得到\(q\)，然后让\(q\)乘以两个矩阵\(W^{q,1}\)和\(W^{q,2}\)得到\(q^{i,1}\)和\(q^{i,2}\)，代表2 heads，以同样的方式处理\(k\)和\(v\)，如下图所示：

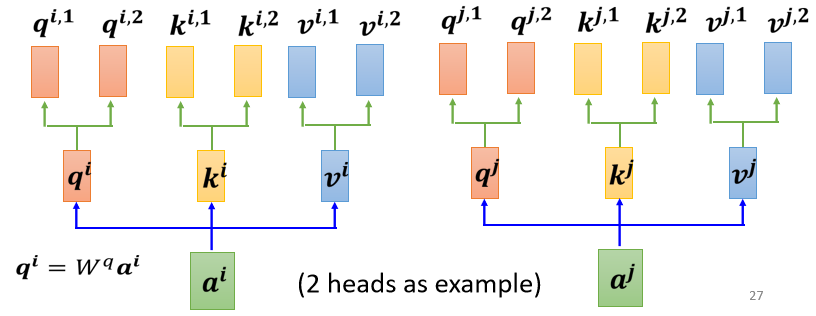
在后续的计算中，我们只将属于相同相关性的矩阵进行运算，如下图所示：

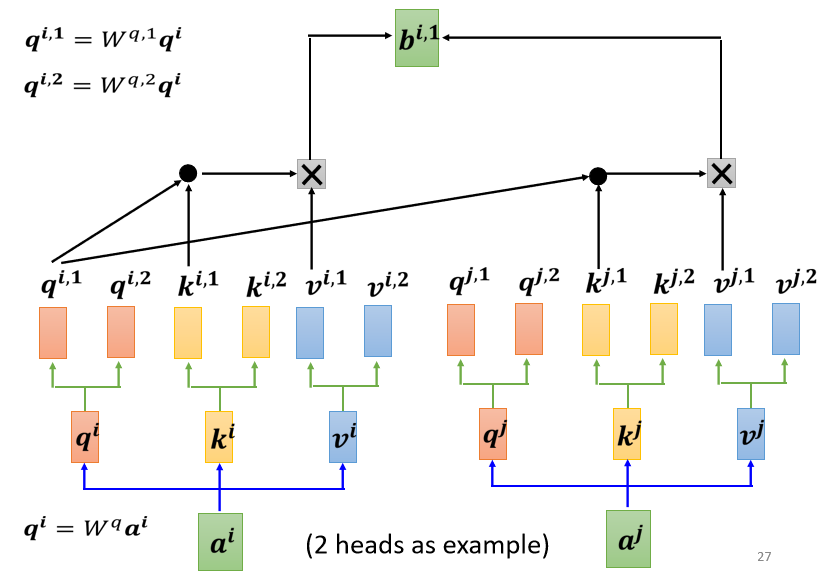
  1. \(q^{i,1}\)分别与\(k^{i,1}\)和\(k^{j,1}\)计算得到\(\alpha_{1,1}^1\)和\(\alpha_{1,2}^1\)。
  2. 然后将\(\alpha_{1,1}^1\)和\(\alpha_{1,2}^1\)分别与\(v^{i,1}\)和\(v^{j,1}\)相乘得到\(b^{i,1}\)。
  3. 我们以同样的方式，得到矩阵\(b^{i,2}\)，将\(b^{i,1}\)和\(b^{i,2}\)拼起来乘以一个矩阵\(W^O\)得到最后的输入\(b^i\)。

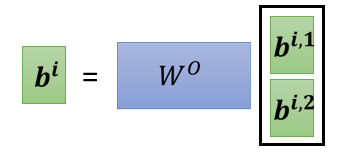
Positional Encoding

通过前边的了解，可以发现对于每一个input是出现在sequence的最前面，还是最后面这样的位置信息，Self-Attention是无法获取到的。这样子可能会出现一些问题，比如在做词性标记（POS tagging）的时候，像动词一般不会出现在句首的位置这样的位置信息还是非常重要的。

我们可以使用positional encoding的技术，将位置信息加入到Self-Attention中。

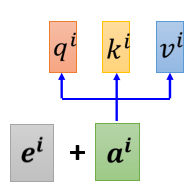
如上图所示，我们可以为每个位置设定一个专属的positional vector，用\(e^i\)表示，上标\(i\)代表位置。我们先将\(e^i\)和\(a^i\)相加，然后再进行后续的计算就可以了。\(e^i\)向量既可以人工设置，也可以通过某些function或model来生成，具体可以查阅相关论文。

参考资料：
《神经网络与深度学习》 邱锡鹏

posted @ 2021-05-04 19:13  sykline  阅读(2654)  评论(2)  编辑  收藏  举报