6-1 最小生成树（普里姆算法）

试实现普里姆最小生成树算法。

函数接口定义：

 

void Prim(AMGraph G, char u);

 

其中 G 是基于邻接矩阵存储表示的无向图，u表示起点

裁判测试程序样例：

 

#include <iostream>
#define MVNum 10
#define MaxInt 32767 
using namespace std;

struct edge{
    char adjvex;
    int lowcost;
}closedge[MVNum];

typedef struct{ 
    char vexs[MVNum];   
    int arcs[MVNum][MVNum]; 
    int vexnum,arcnum;
}AMGraph;
int LocateVex(AMGraph G , char v);//实现细节隐藏
int Min(AMGraph G);//实现细节隐藏
int CreateUDN(AMGraph &G);//实现细节隐藏

void Prim(AMGraph G, char u);

int main(){
    AMGraph G;
    CreateUDN(G);
    char u;
    cin >> u;
    Prim(G , u);
    return 0;
}

/* 请在这里填写答案 */

 

输入样例：

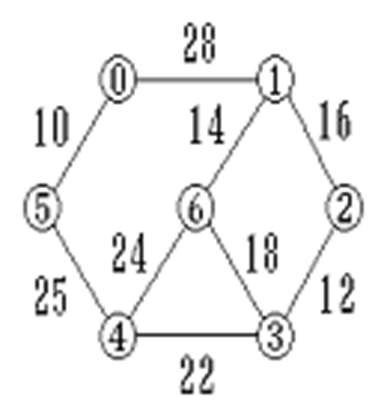
第1行输入结点数vexnum和边数arcnum。第2行输入vexnum个字符表示结点的值，接下来依次输入arcnum行，每行输入3个值，前两个字符表示结点，后一个数表示两个结点之间边的权值。最后一行输入一个字符表示最小生成树的起始结点。

7 9
0123456
0 1 28
0 5 10
1 2 16
1 6 14
2 3 12
3 6 18
3 4 22
4 5 25
4 6 24
0

 

输出样例：

按最小生成树的生成顺序输出每条边。

0->5
5->4
4->3
3->2
2->1
1->6

 

void Prim( AMGraph G, char v )
    { 
        int distance[G.vexnum];
        int parent[G.vexnum];
        //记录v的下标
        int index=0;
        int i,min=MaxInt,imin,count=0;
        // 1.初始化这棵树，即以v为起始点，同时初始化数组distance[]
        //     注：distance数组表示该树的任意一点到该点的最小距离

        //寻找v的下标
        for (i = 0; i < G.vexnum; i++)
        {
            if (G.vexs[i]==v)
            {
                index=i;
            }
            
        }
        for (i = 0; i < G.vexnum; i++)
        {
            if (i==index)
            {
                distance[i]=0;
                parent[i]=index;
            }else
            {
                distance[i]=G.arcs[index][i];
                parent[i]=index;
            }       
        }
        while (1)
        {
            if (count==G.vexnum-1)
            {
                break;
            }
            
            // 2.从小树现有的结点出发，寻找边权值最小的点：
            for ( i = 0; i < G.vexnum; i++){
                if (min>distance[i]&&distance[i]!=0)
                {
                    //记录最小值及其下标
                    min=distance[i];
                    imin=i;
                    
                }
                
            }
            //更新已到达过得节点数
            
            count++;
            // 3.找到后输出该边
            if (count<G.vexnum-1)
            {
                printf("%c->%c\n",G.vexs[parent[imin]],G.vexs[imin]);
            }else
            {
                printf("%c->%c",G.vexs[parent[imin]],G.vexs[imin]);
            }
            
            
            
            
            //初始化min以便下次寻找
            min=MaxInt;
            // 4.将该点的distance数组中的值赋值为0，标记已经遍历过
            distance[imin]=0;
            // 5.循环遍历结点，更新distance[]数组
            for ( i = 0; i < G.vexnum; i++){
                if (distance[i]!=0&&G.arcs[i][imin]<MaxInt)
                {
                    if (distance[i]>G.arcs[i][imin])
                    {
                        distance[i]=G.arcs[i][imin];
                        parent[i]=imin;
                    }                   
                }
            }            
        }
    }