[双栈实现计算器-基于C语言]
双栈实现计算器-基于C语言
数据结构结课了,结课题目中有一道使用栈实现计算器。刚开始看见这道题目就感觉这是一到LeetCode题目,果不其然是LeetCode的227题,基本计算器II。由于我只会一点C语言,所以只能硬着头皮上了。
0.实现思路
先看一个算式的计算过程,例如式子2*(2+2^2-1),这个式子的计算过程当然的先计算'^'的左右操作数,然后再计算'+'左右操作数,再‘-’,最后计算‘*’。根据这个流程,我们可以将算式中的数字依次压入数据栈,将运算符压入运算符栈。
在运算符压栈过程中,需要保持栈顶运算符为当前栈内优先级最高的,换言之就是比当前栈内运算符优先级高的运算符已经完成了运算操作。
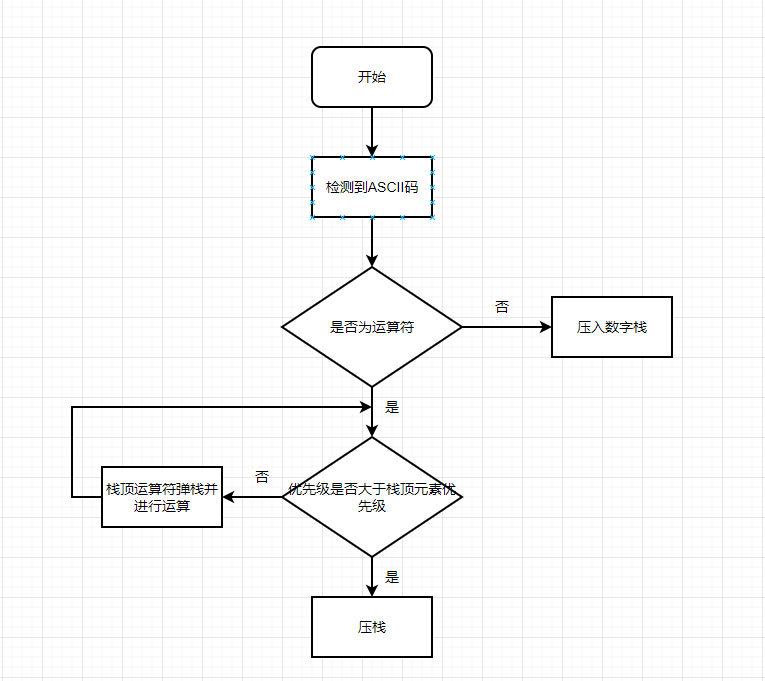
运算操作指的就是根据弹栈得到的运算符,将数字栈进行两次出栈操作的到源数和目的数,根据这三个量进行相应的运算后将结果再压入栈内。
显然,由于括号的存在,括号内运算符的优先级要有顺序并且整体大于括号外运算符的优先级。因此,我在‘(’时将接下来遇到的所有运算符的优先级进行提升,遇见‘)’时将所有运算符优先级恢复,并在检测时对栈顶优先级和当前运算符进行优先级更新。
1.动手开干
1.1构建一个栈
c语言并没有一个类或者一个库包含栈这个数据结构,所以得先从构造一个栈开始。幸好之前我闲的没事把队列和栈都已经写好了,虽然有很多弊端,但也够这次实验使用。
首先,定义一个stack结构体
//file name stack.h
#define STACK_SIZE 50
typedef struct stack
{
int DATA[STACK_SIZE];
int TOP; //栈顶指针
}STACK;
int stack_push(STACK *S,int data);
int stack_pop(STACK *S);我这里只写了入栈和出栈这样的基础操作函数
//file name stack.c
#include "stack.h"
/*压栈
*如果栈已满,则直接返回
*未满则入栈并返回自身
* */
int stack_push(STACK* S,int data)
{
if(S->TOP==(STACK_SIZE-1))
{
printf("this stack is full,cannot to push\r\n");
return -1 ;
}
S->DATA[++S->TOP]=data;
return 0;
}
/*弹栈
*如果栈满,返回-1并报告错误
*
* */
int stack_pop(STACK* S)
{
if(S->TOP == -1)
{
printf("this stack is empty,cannot to pop\r\n");
return -1 ;
}
return S->DATA[S->TOP--];
}
1.2计算器本体
#include "stack.h"
/*
使用两个栈实现四则运算计算器
解题思路如下
创建两个栈,分别用来储存运算符和数字
从左到右遍历整个等式,将整数存入整数栈,
如果当前运算符的优先级不大于栈顶运算符的优先级,将栈顶运算符出栈,从数字栈提取左右操作数
执行运算后将结果进行数字栈压栈,然后再进行优先级对比操作
4+5*(9-6)=
*/
#define equa_length 128
void main_task(char elem); //主任务,完成线程分流
int check_oper(char temp_cache); //判断是否为运算符,返回值为0/1
int oper_process(char temp_cache); //对运算符进行处理,返回值为-1/运算符
int cal_task(int instruct); //根据不同种类运算符进行弹栈后运算
int updata_pri(int pri); //更新当前栈顶运算符的优先级并返回该优先级
void display_out(void); //显示输出
void display_init(void); //初始化显示
/*创建全局变量*/
STACK oper; //创建两个栈,数字栈和操作符栈
STACK num;
STACK* oper_p; //创建两个结构体指针,分别传参用
STACK* num_p;
char temp_cache; //缓冲区临时数据
char equa_arr[equa_length]; //输入等式缓冲
int add_pri=0; //附加优先级,由 '(' ')' 调用
int main()
{
oper_p = &oper; //指针指向结构体
num_p = #
oper.TOP=-1; //栈顶指针初始化
num.TOP=-1;
int p=0;
display_init();
gets(equa_arr); //缓存输入的等式
while(equa_arr[p]!='\0')
{
temp_cache=equa_arr[p++];
main_task(temp_cache);
}
display_out();
return 0 ;
}
/*主流程
*对等式的元素进行分流操作
*无返回值
* */
void main_task(char elem)
{
if(check_oper(elem)) //检测到运算符
{
if(elem=='(') //检测到括号,直接压栈
{
stack_push(oper_p,elem);
}
else{
oper_process(elem);
}
}
else
{
stack_push(num_p,elem-48);
}
}
/*判断实参数据是否为运算符
*如果是,返回true
* */
int check_oper(char oper)
{
switch(oper)
{
case '=' :
return 1;
break;
case '+' :
return 1;
break;
case '-' :
return 1;
break;
case '*' :
return 1;
break;
case '/' :
return 1 ;
break;
case '(' : add_pri+=5;
return 1 ;
break;
case ')' : add_pri-=5;
return 1 ;
break;
case '^' : return 1;
break;
default : return 0;
break;
}
}
/*空栈?压栈
*不断更新栈顶元素,始终保持优先级最高的运算符在栈顶
*若遇到优先级低的元素,将优先级高的元素出栈运算后再入栈
* */
int oper_process(char cache)
{
int elem_oper_pri; //当前运算的优先级
int top_oper_pri; //存储栈顶运算符的优先级
char temp_; //临时运算符
if(oper_p->TOP==-1) //空栈
{
elem_oper_pri=updata_pri(cache);
stack_push(oper_p,cache);
}
else
{
top_oper_pri=updata_pri(oper_p->DATA[oper_p->TOP]);
elem_oper_pri=updata_pri(cache);
if(elem_oper_pri>top_oper_pri) //如果当前运算符优先级大于栈顶运算符优先级,将当前运算符压栈
{
stack_push(oper_p,cache);
temp_=-1;
}
else //目的是将优先级最高的运算符始终置于栈顶
{
while((elem_oper_pri<=top_oper_pri)&&(oper_p->TOP!=-1))
{
temp_= stack_pop(oper_p);
top_oper_pri=updata_pri(oper_p->DATA[oper_p->TOP]);
cal_task(temp_);
}
stack_push(oper_p,cache);
}
}
return temp_;
}
int cal_task(int instruct)
{
int des,src,res;
switch(instruct)
{
case '+' : if(num_p->TOP==0)
{
src=0;
des=stack_pop(num_p);
}
else
{
des=stack_pop(num_p);
src=stack_pop(num_p);
}
res = src + des;
stack_push(num_p,res);
break;
case '-' : if(num_p->TOP==0)
{
src=0;
des=stack_pop(num_p);
}
else
{
des=stack_pop(num_p);
src=stack_pop(num_p);
}
res = src - des;
stack_push(num_p,res);
break;
case '*' : des=stack_pop(num_p);
src=stack_pop(num_p);
res = src * des;
stack_push(num_p,res);
break;
case '/' : des=stack_pop(num_p);
src=stack_pop(num_p);
res = src / des;
stack_push(num_p,res);
break;
case '(' :
break;
case ')' :
break;
case '^' : des=stack_pop(num_p);
src=stack_pop(num_p);
res = pow (src ,des);
stack_push(num_p,res);
break;
default : printf("error:unkowned symbol");
break;
}
}
/*运算符优先级更新
*()具有附加优先级特性
* */
int updata_pri(int pri)
{
int last_pri;
switch(pri) //更新当前栈顶运算符的优先级
{
case '=' : last_pri=0+add_pri;
break;
case '+' : last_pri=2+add_pri;
break;
case '-' : last_pri=2+add_pri;
break;
case '*' : last_pri=3+add_pri;
break;
case '/' : last_pri=3+add_pri;
break;
case '(' : //add_pri+=5;
last_pri=1+add_pri;
break;
case ')' : //add_pri=add_pri-5;
last_pri=1+add_pri;
break;
case '^' : last_pri=4+add_pri;
break;
default : last_pri=-1;
break;
}
return last_pri;
}
void display_out(void)
{
printf("=== res is %d ===\r\n",stack_pop(num_p));
}
void display_init(void)
{
printf("============================================================\r\n");
printf("=== calculator ===\r\n");
printf("=== syh_stack ===\r\n");
printf("=== please input a equation ===\r\n");
printf("=== ");
}2.代码测试
我的vscode出了点问题,只能自己手打gcc指令,测试结果如下
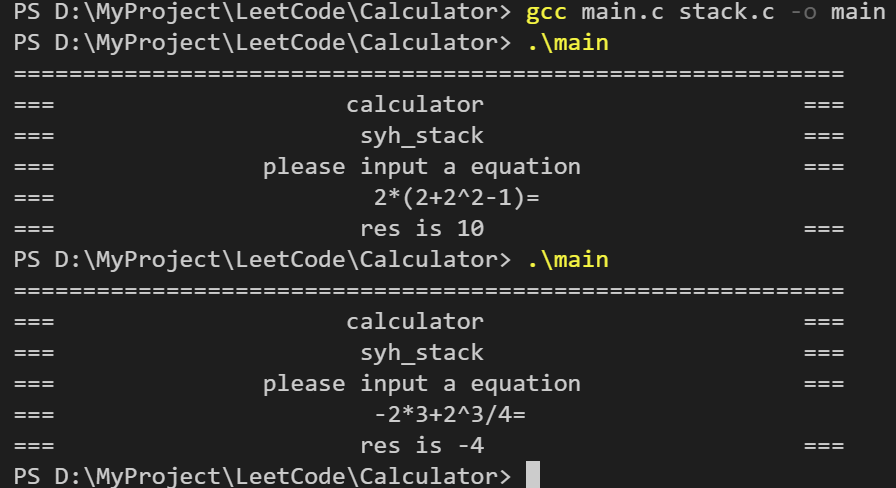
可以看到测试的算式运算结构都没问题。
3.存在的问题
目前存在的问题有
输入字符之间不能有空格,原因是我没有对空格进行过滤,加个空格过滤就ok了
只能进行十以内数字的混合运算,原因是输入使用的是ASCII码,在压入数据栈的时对数据进行加权求和就ok了
输入等式长度受限,这是代码内栈长度宏定义导致的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号