测试「20201015测试总结」
关于这套题:

那么傻逼题是怎么回事呢,小编也不知道。
那么现在就来看看这套题有多傻逼。
T1
这道题是本次考试中最正常的一道。
转换一下思路,将位置 \(i\) 的一个在 \(t\) 时刻出现的物品看做是在 \(t-i\) 时刻在位置 \(0\) 出现。
按在位置 \(0\) 的出现时刻依次考虑所有物品,选出当前已花费时间最少的小车去运送这个物品。
用一个数据结构支持查询最小元素,插入删除元素。
然而这道题题面写的数据范围是:
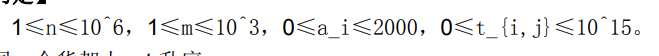
也就是说读入量完全可以达到 \(10^9\) 的级别。然而出题人为了使标程通过,数据最大只有1e7……
\(\text{Code}:\)
#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>
typedef long long lxl;
const int maxn=1e7+5;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
template <typename T>
inline void read(T &x)
{
x=0;T f=1;char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
x*=f;
}
int n,m,cnt;
lxl A[maxn],ans;
std::priority_queue<lxl,std::vector<lxl>,std::greater<lxl> > q;
int main()
{
#ifndef ONLINE_JUDGE
freopen("Shipment.in","r",stdin);
// freopen("Shipment.out","w",stdout);
#endif
read(n),read(m);
for(int i=1,a;i<=n;++i)
{
read(a);
while(a--)
{
read(A[++cnt]);
A[cnt]-=i*1ll;
}
}
std::sort(A+1,A+cnt+1);
while(m--) q.push(0);
for(int i=1;i<=cnt;++i)
{
lxl t=q.top();q.pop();
q.push(std::max(t,A[i])+n+1);
ans=std::max(ans,std::max(t,A[i])+n+1);
}
printf("%lld\n",ans);
return 0;
}
T2
LCT裸题,不说了。
考试时写link操作时没写access,导致复杂度假了,爆成80pt。
然而试卷开头的大标题是 \(\text{NOIP}\text{模拟赛}\) ,要是NOIP它真的考了LCT,我倒立做东方鬼畜音mad。
\(\text{Code}:\)
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#define Rint register int
#define INF 0x3f3f3f3f
// using namespace std;
typedef long long lxl;
const int maxn=2e5+5;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
template <typename T>
inline void read(T &x)
{
x=0;T f=1;char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
x*=f;
}
int q,online;
int tot;
int val[maxn],siz[maxn];
int fa[maxn],ch[maxn][2];
inline bool nroot(int p) {return ch[fa[p]][0]==p||ch[fa[p]][1]==p;}
inline bool get(int p) {return ch[fa[p]][1]==p;}
inline void update(int p)
{
siz[p]=siz[ch[p][0]]+siz[ch[p][1]]+val[p];
}
inline void rotate(int p)
{
int f=fa[p],gf=fa[f],tmp=get(p);
if(nroot(f)) ch[gf][ch[gf][1]==f]=p;
if(ch[p][tmp^1]) fa[ch[p][tmp^1]]=f;
ch[f][tmp]=ch[p][tmp^1];
ch[p][tmp^1]=f;
fa[f]=p;
fa[p]=gf;
update(f);
}
inline void splay(int p)
{
for(int f=fa[p];f=fa[p],nroot(p);rotate(p))
if(nroot(f)) rotate(get(p)==get(f)?f:p);
update(p);
}
inline void access(int x)
{
for(int y=0;x;x=fa[y=x])
{
splay(x);
ch[x][1]=y;
update(x);
}
}
inline void link(int x)
{
fa[++tot]=x;
val[tot]=siz[tot]=1;
access(tot);
splay(tot);
}
inline void erase(int x)
{
access(x);
splay(x);
val[x]=0;
update(x);
}
inline int kth(int p,int k)
{
while(p)
{
if(k<=siz[ch[p][0]]) p=ch[p][0];
else if(k==siz[ch[p][0]]+val[p]) return p;
else k-=siz[ch[p][0]]+val[p],p=ch[p][1];
}
return 0;
}
inline int query(int x,int y)
{
access(x);
splay(x);
return kth(x,siz[x]-y);
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("maintain.in","r",stdin);
freopen("maintain.out","w",stdout);
#endif
read(q),read(online);
int lasans=0;
int opt,x,y;
val[1]=siz[1]=1;
tot=1;
while(q--)
{
read(opt);
if(opt==1)
{
read(x);
if(online) x^=lasans;
if(!x||x>tot||!val[x]) continue;
link(x);
if(online) lasans=x;
}
else if(opt==2)
{
read(x);
if(online) x^=lasans;
if(!x||x>tot||!val[x]) continue;
if(online) lasans=query(x,1);
erase(x);
}
else
{
read(x),read(y);
if(online) x^=lasans,y^=lasans;
if(!x||x>tot||!val[x]) continue;
int ans=query(x,y);
if(online) lasans=ans;
printf("%d\n",ans);
}
}
return 0;
}
T3
判断相似三角形……
出题人没有*
没打,看过OIWiki出题相关的正常出题人都不会出这样的SB题。

