信息论

1、采样

把模拟信号变成数字信号的过程称之为采样。

现实世界是连续的，但，计算机在时间和空间上都是离散的。

为了让计算机能够处理真实的物理信号，需要把连续的物理信号离散化。我们习惯上把连续信号时间的离散化叫做采样，而把幅度上的离散化叫做量化，采样定理研究的是时间离散化的问题。

2、卷积定理

时域卷积等于频域相乘，频域相乘等于时域卷积。

翻折=卷积

卷积定理的理解，参考：
https://zhuanlan.zhihu.com/p/41609577

3、采样定理

为了不失真地恢复模拟信号，采样频率应该大于(没有等号)模拟信号频谱中最高频率的2倍。 　fs > 2fmax

【注意，百科有等号，是错的。工程中，正常也不会冒险去取临界值，取临界值不是找死嘛】

书上写的是大于或等于，是不是不够严谨
应该没有等于才对，等于时刚好发生混叠，奥本海默那本里面就没等于
怪不得！我迷惑了好久，原来是课本错了

（1）简单理解

工程上总要把波展开成傅里叶级数，也就是正弦函数。
正弦的函数表达式如下，其中A是振幅， ω 是角频率， ϕ 是初相，也就是有三个常量就能唯一确定一个正弦信号：y(t)=Asin(ωt+ϕ)
一个函数三个未知数，所以需要代入三个不同的点解出三个未知数，得到唯一的表达式，所以一个周期需要取三个以上的点才能完美采样。

从图像上也能直观看出来：在等时间间隔的情况下，如果采样间隔恰好是正弦信号周期的一半，也就是一个信号周期内能采集到两个点，如果恰好采样到的两个点幅值都是0，那就恰好无法计算出正弦信号的表达式。
如果采样间隔比信号周期的一半还要小，那么一个信号周期内至少能采集到三个点，一定能够计算出正弦信号的表达式。

所以我们可以这么说：如果采样的时间间隔小于被采样正弦信号周期的一半，我们一定能无失真的恢复出被采样信号。

工程上大多数信号都能展开成若干正弦信号叠加，如果我的采样间隔能够完美采样周期最短的那个正弦信号，那当然能完美采样这个由若干正弦叠加出来的信号。

采样间隔的倒数是采样率，信号周期的倒数是信号频率，这样都倒过来，就得到了我们最常见的采样定理表达方法：当采样率大于被采样信号中频率最高信号频率的2倍时，采样后的信号能完美保留被采样信号的所有信息。

这解释，简直完美呀！大佬就是大佬，三点确定一个正弦函数，太通俗易懂了！

参考：
https://www.zhihu.com/question/431920644/answer/1597049082

（2）理论理解【无法理解】

对一个连续信号的采样，采样后的频谱相当于将采样前的频谱进行了延拓，延拓的周期就是采样频率。

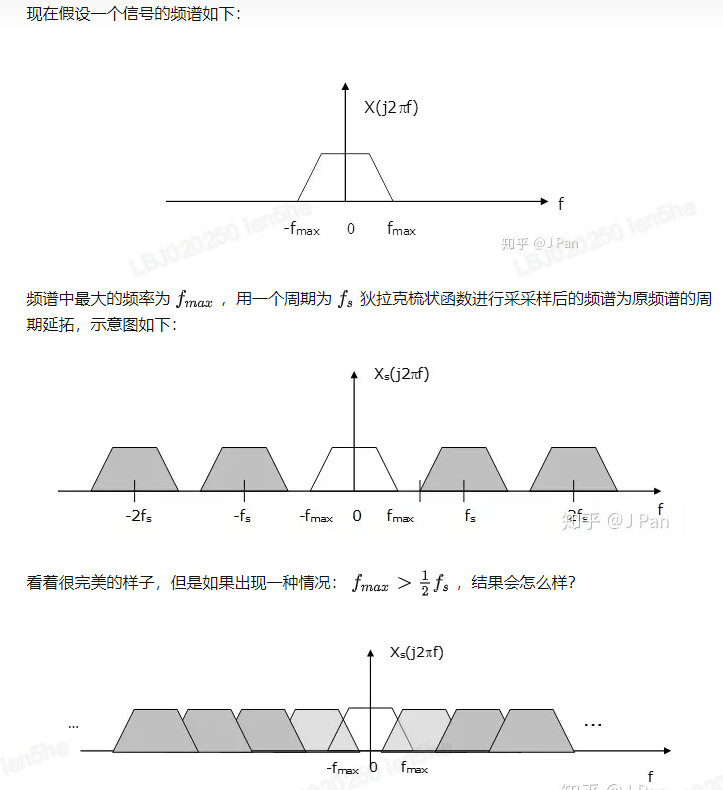
也就是说，原始频谱信号经过周期延拓后会有一部分重叠，这样在重叠的部分就会有信息的丢失，也就无法进行信号复原了，也就是说，对于连续信号的进行抽样离散的话，必须保证采样频率是原连续信号最大频率分量的2倍频率以上，否则信号就难以复原。这就是采样定理，又叫奈奎斯特采样定理或香农采样定理。

如果不能满足上述采样条件，采样后信号的频率就会重叠，即高于采样频率一半的频率成分将被重建成低于采样频率一半的信号。这种频谱的重叠导致的失真称为混叠，而重建出来的信号称为原信号的混叠替身，因为这两个信号有同样的样本值。

采样定理的理解，参考：
https://zhuanlan.zhihu.com/p/45114376

4、带通采样定理

大佬，可以再通俗讲一下小于2倍采样时候的频谱混叠吗

哦，说带通采样定理啊，这个要直观去理解确实不容易，很多东西是从数学出发推导出来的，包括频带的翻折其实也是傅里叶变换的基本性质，时域两个信号相乘，等价于频域两个信号卷积嘛，这个频带翻折本质就是卷积，说翻折更直观一些（是的，我们都讨厌卷积）。
混叠也是同样的道理，经过卷积以后，被采样信号的频谱是被不断复制粘贴的，如果粘贴的各个副本没有重叠在一起，它们可以被区分开，那就可以用滤波器把这个频谱唯一恢复出来，这就是没有混叠；而混叠时，副本之间互相重叠了，重叠区域无法区分开，就没有办法用滤波器唯一恢复出来。

我觉得可以这么去理解，不混叠的意思就是能够唯一表示，如果不能唯一表示那就是混叠了。举一个例子就容易理解，比如很多人会纠结的恰好等于2倍采样率时会不会混叠，那就找一个最典型的，恰好采到正弦信号t=0和t=pi的位置，两个点都是0，根据周期性还可以推算出t=2pi时也是0，t=3pi时也是0...这下好了，我采到的究竟是一个正弦呢还是一个直流？也就是当采样率恰好是信号频率2倍时，采样后的信号和直流(频率为0)混在一起区分不开了，这就是混叠。

参考：还是 @蒋宇辰 大佬的评论区
https://www.zhihu.com/question/431920644