机器学习，评估——风险函数

1.损失函数vs风险函数

损失函数度量模型一次预测的好坏，风险函数度量平均意义下模型预测的好坏。

2.风险函数定义

风险函数（risk function）=期望风险（expected Risk）=期望损失（expected loss），可以认为是平均意义下的损失。

例如：下面的对数损失函数中，损失函数的期望，就是理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失。

风险函数有两种，不考虑正则项的是经验风险（Empirical Risk），考虑过拟合问题，加上正则项的是结构风险（Structural Risk）。

监督学习的两种基本策略：经验风险最小化（ERM）和结构风险最小化（SRM）。

这样，监督学习问题就变成了经验风险或结构风险函数的最优化问题（1.11）和（1.13）。经验或结构风险函数是最优化的目标函数。

（1）三个风险的关系

期望风险是理想，是白月光，是可望不可求的，只能用经验风险去近似，而结构风险是经验风险的升级版。

为什么可以用经验风险估计期望风险呢？

根据大数定律，当样本容量N趋于无穷时，经验风险R_emp(f)趋于期望风险R_exp(f)。所以一个很自然的想法是用经验风险估计期望风险。

但是，由于现实中的训练样本数目有限，甚至很小，所以用经验风险估计期望风险常常并不理想，要对经验风险进行一定的矫正。这就关系到监督学习的两个基本策略：经验风险最小化和结构风险最小化。

（2）期望风险（expected Risk）【全局，理想】

期望风险对所有样本预测错误程度的均值，基于所有样本点损失函数最小化。期望风险是全局最优，是理想化的不可求的。

期望风险=期望损失=风险函数，也就是损失L(Y,f(X))的数学期望，在理论上，可以代入期望公式EX=∑xi·Pi=∫x·f(x)dx，也就是E(L(Y,f(X))=∫L(y,f(x))·f(x,y) dxdy。

但是由于联合概率密度函数f(x,y)不知道，所以此路不通，只能另寻他路，也就是根据经验找近似。【这个矛盾，可以在文末的一张图上体现】

（3）经验风险（Empirical Risk）【局部，现实】

经验风险，基于训练集所有样本点损失函数的平均最小化。经验风险是局部最优，是现实的可求的。

经验风险=经验损失=代价函数

给定一个数据集，模型f(x)关于训练集的平均损失被称为经验风险(empirical risk)或经验损失(empirical loss)。

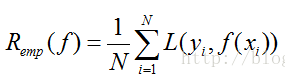
这个公式的用意很明显，就是模型关于训练集的平均损失（每个样本的损失加起来，然后平均一下）。在实际中用的时候，我们也就很自然的这么用了。

（4）结构风险（Structural Risk）

结构风险，就是在经验风险上加上一个正则化项（regularizer）或者叫做罚项（penalty term），即

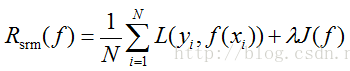
3.经验风险最小化和结构风险最小化

（1）经验风险最小化&结构风险最小化

经验风险最小化（empirical risk minimization，ERM），就是认为经验风险最小的模型是最优的模型，用公式表示：

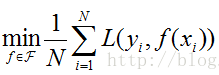
这个理论很符合人的直观理解。因为在训练集上面的经验风险最小，也就是平均损失越小，意味着模型得到结果和“真实值”尽可能接近，表明模型越好。

 

当样本容量不大的时候，经验风险最小化模型容易产生“过拟合”的问题。为了“减缓”过拟合问题，就提出了结构风险最小的理论。

结构风险最小化（structural risk minimization，SRM），就是认为，结构风险最小的模型是最优模型，公式表示：

 

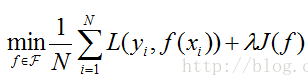
（2）经验风险最小化的例子：极大似然估计（maximum likelihood estimation）。

模型，条件概率分布；

损失函数，对数损失函数；

　　经验风险最小化等价于极大似然估计。

（2）结构风险最小化的例子：贝叶斯最大后验概率估计。

模型，条件概率分布；

损失函数，对数损失函数；

模型复杂度，由先验概率表示；

结构风险=经验风险+正则项=后验概率+先验概率；

先验概率不变，结构风险最小化，等价于最大后验概率估计。

 

4.风险函数与对数损失函数

 

 

 

参考：

李航《统计学习方法》

https://blog.csdn.net/xierhacker/article/details/53366723?utm_source=copy

（structural risk minimization，SRM）