机器学习，优化——如何找到最优学习率

 

1.找到最优学习率的方法

（1）笨方法——指数提高学习率

从0.0001开始尝试，然后用0.001，每个量级的学习率都去跑一下网络，然后观察一下loss的情况，选择一个相对合理的学习率，但是这种方法太耗时间了。

（2）简单的启发方法【有时间总结】

参考：https://arxiv.org/pdf/1506.01186.pdf，3.3节

（3）皮尔森检测法筛选最优学习率

读：《深度学习用于天文图像空间碎片和恒星分类》

2015 年 Leslie N. Smith 在其论文里提出了一种选择学习率的方法，就是从一个最低的学习率开始训练网络，依次指数提高学习率，然后画出损失图，可以有效地选取最优学习率。（Cyclical Learning Rates for Training Neural Networks）这是一个可行的方法，但仍有一定的不确定性。【这应该就是（1）指数提高学习率】

我们所搭建的神经网络的权重一开始是随机产生的，就像一幅地图，出生的位置是随机的，但目的地却是唯一的，这样单次的成功并不意味着这个学习率就是最好的，随机性导致的不确定性使得我们要考虑寻找一个更加稳定的学习率参数。本文选用的是皮尔森检验的筛选学习率参数的方法。

在最开始的试验中，我们采用逐步下降的学习率来训练我们的卷积神经网络模型，但都没有取得良好的结果。于是，改变策略采用固定的学习率。

固定学习率几个好处：首先在学习率足够低的情况下具有更高的概率收敛到局部最优解。其次是每次训练的时间较为稳定，不会有剧烈的波动。虽然固定的学习率在机器学习中很少被使用到，但是本文处理数据的特殊性，恰巧适用这种方法。
虽然现在大量的搭建神经网络的文章使用的也是固定的学习率，但是目前并没有明确的计算公式，大都是根据经验来定学习率参数。

在本文里，我们使用皮尔森检验法来筛选可用的学习率。由于最初的参数是随机的，所以即使同一学习率也会出现有的时候可以训练成功，有的时候训练失败。对此，我们使用皮尔森检测的目的就是筛选成功概率最高的学习率。首先假设： 

Η0：每次试验训练的成功收敛的概率大于等于 0.8。
皮尔森检测公式为：

 

其中k = 2，𝑝₁= 0.8，n = 5，𝑝₂= 0.2, 经查表得𝜒²_0.05 = 3.84，带入公式里面计算得当𝑛_𝑖大于等于 2.25 的时候才能满足𝜒²< 𝜒²_0.05(1)。所以，我们可以得出结论，只有当 5 次实验中成功 3 次及以上才能确定该学习率满足Η0条件，即每次试验训练的成功收敛概率大于等于 0.8。

经过皮尔森检测的结果，我们在寻找合适的学习率的原则就是驯练五次，成功收敛三次即是合格。之后把经筛选出的合格的学习率再每一组挑选训练时成功收敛的 20 组结果来计算最后的分类正确率，取正确率高的一组为最后选取的学习率参数。【不理解，为什么是20个为一组？？】 

2.学习率重要性

目前深度学习使用的都是非常简单的一阶收敛算法，梯度下降法，不管有多少自适应的优化算法，本质上都是对梯度下降法的各种变形，所以初始学习率对深层网络的收敛起着决定性的作用，w=w−α∂loss(w)/∂w

 

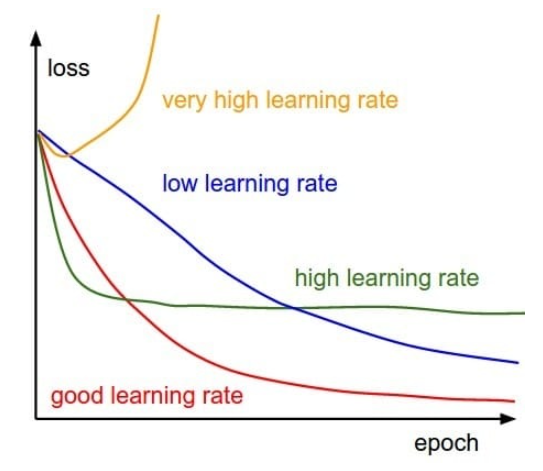
如果学习率太小，会导致网络loss下降非常慢，如果学习率太大，那么参数更新的幅度就非常大，就会导致网络收敛到局部最优点，或者loss直接开始增加，如下图所示。

 

 

 

参考：

https://blog.csdn.net/whut_ldz/article/details/78882871

梯度下降算法：https://blog.csdn.net/hrkxhll/article/details/80395033

http://www.imooc.com/article/details/id/32412