机器学习，评估——模型评估

模型评估包括模型准确性评估和模型泛化性能评估。

一、模型准确性

1.两种评价标准

我们以Y={y1,y2,...,yn}Y={y1,y2,...,yn}表示真实的数据，以Y^={y^1,y^2,...,y^n}Y^={y^1,y^2,...,y^n}表示预测出来的数据。

（1）最小错误率（最大准确率）

（1.1）回归问题的性能度量：

均方误差（mean squared error，MSE）：对应损失函数Mean Squared Error Loss，也称为 L2 Loss

                

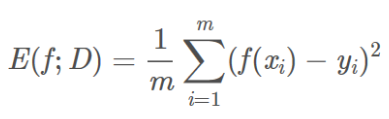
均方根误差（root mean squared error，RMSE）：MSE开根号

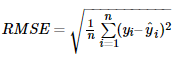
平均绝对误差（mean absolute error，MAE）：对应损失函数Mean Absolute Error Loss，也称为 L1 Loss

       

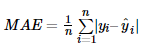
均方对数误差（mean squared logarithmic error，MSLE）：

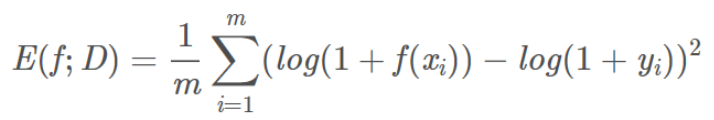
均方根对数误差（root mean squared logarithmic error，RMSLE）：

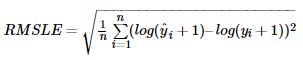
使用RMSLE的好处一：

　　假如真实值为1000，若果预测值是600，那么RMSE=400， RMSLE=0.510

　　假如真实值为1000，若预测结果为1400， 那么RMSE=400， RMSLE=0.336

　　可以看出来在均方根误差相同的情况下，预测值比真实值小这种情况的错误比较大，即对于预测值小这种情况惩罚较大。

使用RMSLE的好处二：

　　直观的经验是这样的，当数据当中有少量的值和真实值差值较大的时候，使用log函数能够减少这些值对于整体误差的影响。

平方损失（squared loss） ：不是MSE，又叫，平方损失函数（quadratic loss function）。

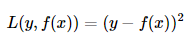
绝对误差（absolute Loss）：不是MAE，又叫，绝对值损失函数（absolute loss function）。

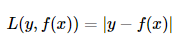
决定系数（coefficient of determination）：

 

Huber Loss：

 

（1.2）分类任务常用性能度量：

准确率和错误率，既适用于二分类也适用与多分类。

信息检索、Web搜索等场景中经常需要衡量正例被预测出来的比率或者预测出来的正例中正确的比率，此时查准率和查全率比错误率和精度更适合。

混淆矩阵：

 

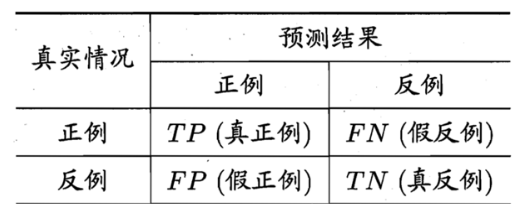
准确率（Accuracy）（精度？）：

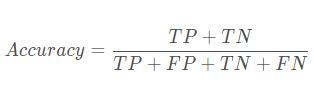
错误率：错误分类的样本数占总样本数的比例

Error = 1-Accuracy = (FP+FN) / (TP+FP+TN+FN)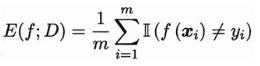       

查准率、精确率（Precision）：正例被模型预测为正例的总数/被预测为正例的总数

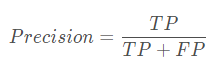
查全率、召回率（Recall）：正例被模型预测为正例的总数 与 原本正例的总数

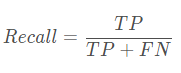
查准率和查全率是一对矛盾的度量。一般，查准率高时，查全率偏低；而查全率高时，查准率偏低。 根据查准率和查全率，有了查准率-查全率曲线，即P-R曲线。

P-R曲线：直观地显示出模型在总体上的查全率、查准率。

现实任务中的P-R曲线常是非单调、不平滑的，在很多局部都有上下波动。

当有多个模型时，我们可以在将多个模型的P-R曲线画在一起，若一个模型被另一个模型完全包住，则可说明后者模型优于前者，但如果两个曲线发生交叉，则无法判断哪个更优。【外层的模型更优】

F1值：

P和R是矛盾的，综合考虑，最常见的方法是F-Measure了，也叫F-Score。F1综合了Precision和Recall的结果，当F1较高时则说明模型更优。

F1值 = 2*查准率 * 查全率 / (查准率 + 查全率)        

ROC：受试者工作特征（ROC）曲线是另一个二分类器常用的工具。

与P-R曲线很相似，ROC曲线是真正例率（True Positive Rate,TPR,也是查全率）对假正例率（False Positive Rate, FPR）的曲线。ROC曲线横坐标为假正例率，纵坐标为真正例率。

        

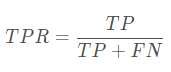
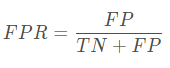
如果两个模型画在ROC曲线图上，应该如何去评价两者的性能，此时如果一定要进行比较，则较为合理的判据是比较ROC曲线下的面积。

AUC（Area Under Roc Curve，ROC曲线下的面积）：AUC就是对ROC曲线下各部分的面积之和。

AP与mAP（mean Average Precision）：用于多标签图像分类。mAP虽然字面意思和mean  accuracy看起来差不多，但计算更繁琐。

AP衡量的是学出来的模型在每个类别上的好坏，mAP衡量的是学出的模型在所有类别上的好坏，mAP是所有AP的平均值。

（2）最小风险（代价敏感错误率）

现实任务中不同类型的错误所造成的后果很可能不同，为了权衡不同类型错误所造成的不同损失，可为错误赋予“非均等代价”。

代价敏感错误率与代价曲线：？？

 

下面是4个性能度量指标的详细说明。

2.常用性能度量（详细）

（1）均方误差（mean squared error, MSE）

以线性回归为例说明。（术语“线性回归”用来指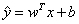，截距项b常称为仿射变换的偏置(bias)参数。仿射函数，即最高次数为1的多项式函数，常数项为0则为线性函数。）

我们的目标是建立一个系统，将向量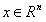作为输入，预测标量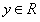作为输出。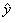表示模型预测y应该取的值。定义输出为线性函数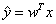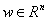，是参数向量。

（1.1）MSE

是度量模型性能的一种方法，计算模型在测试集上的均方误差。（测试误差=泛化误差）

当预测值与目标值之间的欧几里得距离增加时，误差增加。

 （1.2）如何最小化MSE(test)？

为了构建一个机器学习算法，需要设计算法，通过观察训练集( x(train) , y(train) )获得经验，减少MSE(test)以改进权重w。

一种直观方式是最小化训练集均方误差MSE(train)。

我们可以简单求解其导数为0的情况：

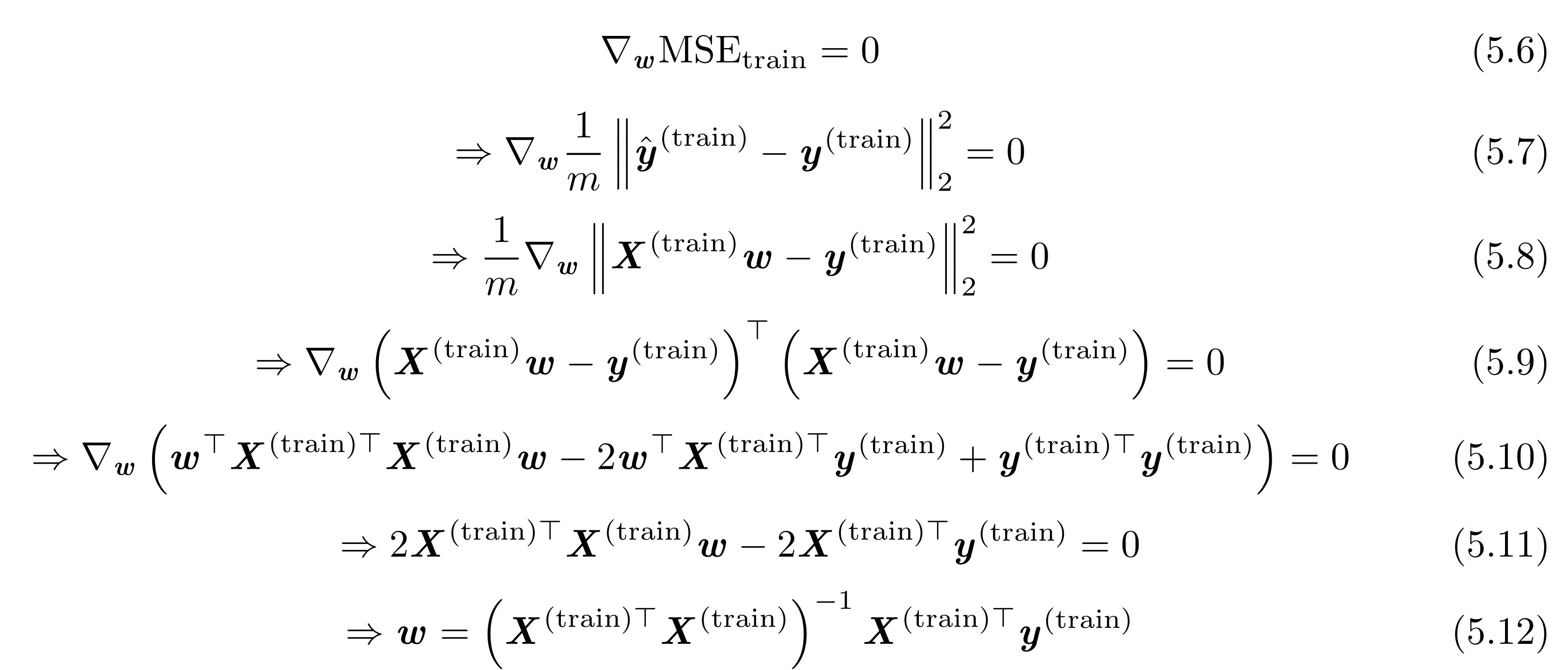
这里的m是训练集的样本数，其实应该写成m(train)。

X是输入设计矩阵，

5.10到5.11，用到了向量和矩阵求导公式。5.6-5.12就是在MSE(train)取极小值时（导数=0），求解w的过程。

5.12是正规方程（normal equation），代入数值就是w的最优解，也就是MSE(train)取最小值时对应的w值。

（2）准确率和错误率

 

（3）查准率和查全率

 

（4）代价敏感错误率

类似于决策规则之——最小风险的贝叶斯决策。

风险函数（损失函数），通常是决策和自然状态的函数，可用决策表（决策矩阵）来表示。

 

 

下面的代价矩阵相当于决策表。

 

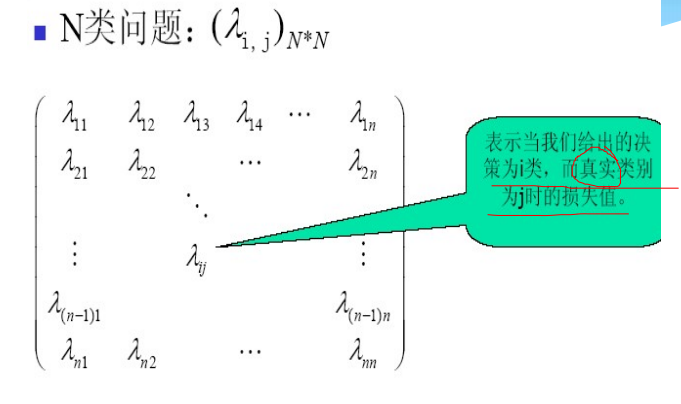
二、模型泛化性能

通过实验可以估计学习算法的泛化性能，而“偏差-方差分解”可以用来帮助解释泛化性能。偏差-方差分解试图对学习算法期望的泛化错误率进行拆解。 

 

 

 

 

参考：

Ian Goodfellow、Yoshua Bengio 和Aaron Courville《深度学习》

https://www.cnblogs.com/jiaxin359/p/8989565.html

https://blog.csdn.net/weixin_43532000/article/details/104995734

https://blog.csdn.net/weixin_43198141/article/details/89392675

https://lipidong.blog.csdn.net/article/details/79109311#comments