机器学习，评估——熵（交叉熵）

1.信息熵

①H(x) = - ∑  p(xi)  log p(xi)

②熵是不确定性的度量，越不确定，越混乱，熵越大。

③越平均的时候，熵越大。

2.交叉熵

①两个概率分布p(x)和q(x)，p分布已知，q未知，交叉熵函数就是两个分布的互信息，反应其相关程度，交叉熵越小越相关，两个分布越接近，分类器效果越好。所以机器学习中，经常拿交叉熵来做为损失函数(loss function)。

②表示使用估计的分布q(x)对来自真实分布p(x)的样本进行编码，所需要的平均长度。交叉熵大于等于真实分布的信息熵（最优编码）。

③H(p,q) = - ∑  p(xi)  log q(xi)

例子：

x的概率分布为：{1/4 ，1/4，1/4，1/4}，现在我们通过机器学习，预测出来二组值：

y1的概率分布为 {1/4 , 1/2 , 1/8 , 1/8}

y2的概率分布为 {1/4 , 1/4 , 1/8 , 3/8}

从直觉上看，y2分布中，前2项都100%预测对了，而y1只有第1项100%对，所以y2感觉更准确，看看公式算下来，是不是符合直觉：

对比结果，H(x,y1)算出来的值为9/4，而H(x,y2)的值略小于9/4，故y2更准确，符合直觉。

 

3.相对熵(KL散度)

①未知分布p(x)，用已知分布q(x)来估计，KL散度表示两个分布之间的距离。

②相对熵表示用估计分布计算的平均编码长度比最短平均编码长度长多少。相对熵 = 交叉熵 - 信息熵。

     KL(p||q) = H(p,q) - H(p)

③它有不好的地方，就是它是不对称的。

举个例子，比如随机变量X∼P取值为1,2,3时的概率分别为[0.1,0.4,0.5]，随机变量Y∼Q取值为1,2,3时的概率分别为[0.4,0.2,0.4]，则：

 

 

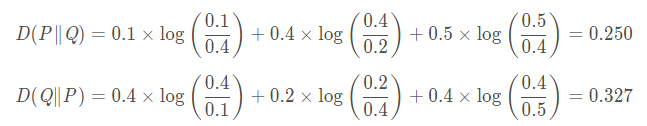
也就是用P来拟合Q和用Q来拟合P的相对熵居然不一样，而他们的距离是一样的。这也就是说，相对熵的大小并不跟距离有一一对应的关系。这点蛮头疼的，因为一般我们希望距离越远下降越快，而相对熵取哪个为参考在同等距离情况下下降的速度都不一样，这就非常尴尬了。

 

既然如此，那为什么现在还是很多人用相对熵衍生出来的交叉熵作为损失函数来训练神经网络而不直接用距离相关的均方差呢？

 

参考：https://blog.csdn.net/weixinhum/article/details/85064685

 

 

4.互信息（信息增益）

①两个随机变量X,Y的互信息，定义为：X,Y的联合分布P(X,Y)与乘积分布P(X)P(Y)的相对熵：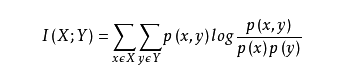
 

②也就是用乘积分布P(X)P(Y)与联合分布的交叉熵，减去联合分布的信息熵，就是互信息，过程如下：

乘积分布：q(x,y) = p(x) p(y)

I (X;Y) = H(p(x,y),q(x,y)) - H(p(x,y))

           = - ∑p(x,y) log q(x,y) - [ -∑ p(x,y) log p(x,y) ]

           = ∑ p(x,y) log p(x,y) - ∑p(x,y) log q(x,y)

           = ∑ p(x,y) log p(x,y) / q(x,y)

           = ∑ p(x,y) log p(x,y) / p(x)p(y)

③还不好理解，就可以看如下图示：

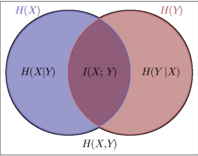
相当于一种不严谨的说法就是：(X+Y)−X⋃Y=X⋂Y
或许另一种等价的定义好理解：I(X;Y)=H(X)−H(X∣Y)

上面这个公式表示的就是，在Y已知的条件下，X的信息量减少的多少。也就是决策树中的信息增益。

其实两种定义是等价的：

 

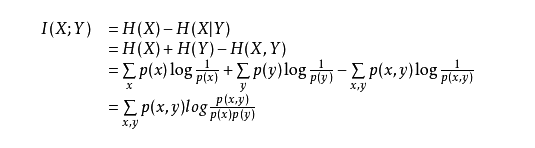
5.互信息、信息增益区别：（二者本质/值相同）

1）两者描述的时空不同
Gain=H（X）-H(X/Y)， 意义是系统分类后增加的信息量（研究同一系统的不同状态）
I（X,Y）=H(X)-H(X/Y)=H(Y)-H(Y/X)，意义就是X与Y之间对应关系的信息量
（研究同一状态下系统中的两个子系统）
2）Y的含义不一样
增益里面Y是分类方式，互信息里面Y是事件
互信息里面的Y，用H（Y）表示，可以通过统计测量概率，并用信息熵公式计算。
但是增益里面的Y，由于是一种分类方式，它的熵要是直接计算，信息论里面没有介绍。
3）两者之间的关系
信息增益是描述前后两种不同状态的信息熵变化，即确定性的增加量，分类本质就是将一个系统中各种元素之间的分类关系（X,Y,Z,...）确定下来。
4）总结
Gain是各元素之间的人为定义的关系信息，I只是两两之间客观关系信息，当然I也能够扩展，通过扩展可以计算得到gain，不论是I还是gain他们都是关系信息，而非事件信息。

5）信息增益指的是经验熵和经验条件熵的差值，经验熵和经验条件熵是通过样本进行极大似然估计得出来的，是一个估计值的差。

6）互信息指的是 熵和条件熵， 是对总体的信息量的评价，不是估计值。信息增益是互信息的无偏估计，所以在决策树的训练过程中， 两者是等价的。

 

6.交叉熵、相对熵区别

1）信息熵：编码方案完美时，最短平均编码长度的是多少。
2）交叉熵：编码方案不一定完美时（由于对概率分布的估计不一定正确），平均编码长度的是多少。
平均编码长度 = 最短平均编码长度 + 一个增量
3）相对熵：编码方案不一定完美时，平均编码长度相对于最小值的增加值。（即上面那个增量）

 

 

参考：

https://blog.csdn.net/qq_41978536/article/details/89016305

https://www.zhihu.com/question/39436574/answer/85748573