矩阵理论

1. 范数

（1）常用向量范数

L0范数：||X||₀，向量中所有非零元素个数

L1范数：||X||₁向量所有元素绝对值之和

L2范数：||X||₂，向量各个元素的平方求和然后求平方根，向量长度，欧几里得范数。常省略表示为||X||，值大小与向量模长|X|相同。

　　　　对每个元素导数与整个向量有关（导数：xi/||X||₂）

平方L2范数：即L2范数的平方

　　　　对每个元素的导数只取决于对应元素（导数：2xi）

Lp范数：||X||p，向量各个元素绝对值的p次方求和然后求1/p 次方，p取值范围[0,+∞) 

L∞范数：||X||∞，向量各个元素最大的绝对值，最大范数。||X||∞=max(|x1|,|x2|,⋯,|xn|)

L+∞范数：表示数据中的最大值

L-∞ 范数：表示数据中的最小值

 

 

（2）常用矩阵范数

 

Frobenius范数：||A||F，矩阵各个元素的平方求和然后求平方根，衡量矩阵大小，类似于向量的L2范数。又叫矩阵模长、矩阵的范数，常省略表示为||A||。

 

 

 

 （3）向量范数定义

 

 

 

（4）矩阵范数定义

 

 

 

 

2.向量和矩阵的求导公式

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

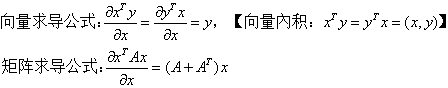
参考：

https://www.cnblogs.com/Kalafinaian/p/11143995.html
https://blog.csdn.net/chenisok/article/details/80358330