A*寻路算法__001_理论

1、了解A星寻路是用来解决什么问题的

　　A*寻路就是用来计算玩家行进路径的，通过它可以计算出避开阻挡的最短路径。

2、了解A*寻路的基本原理

　　不停的找自己周围的点选出一个新的点作为起点再循环的找

3、A*寻路的详细原理

　　1)、寻路消耗公式

　　　　f = g + h  (f：寻路消耗 g:离起点的距离 h:离终点的距离)

　　2)、开启列表

　　　　每次从新的点找周围的点时，如果周围的点已经在开启列表或者关闭列表中了，我们就不去管它了

　　3)、关闭列表 

　　　　每次往关闭列表中放点时我们都应该判断这个点是不是和终点一样，如果是一样证明路径找完了，如果不一样继续找。

　　4)、格子对象的父对象

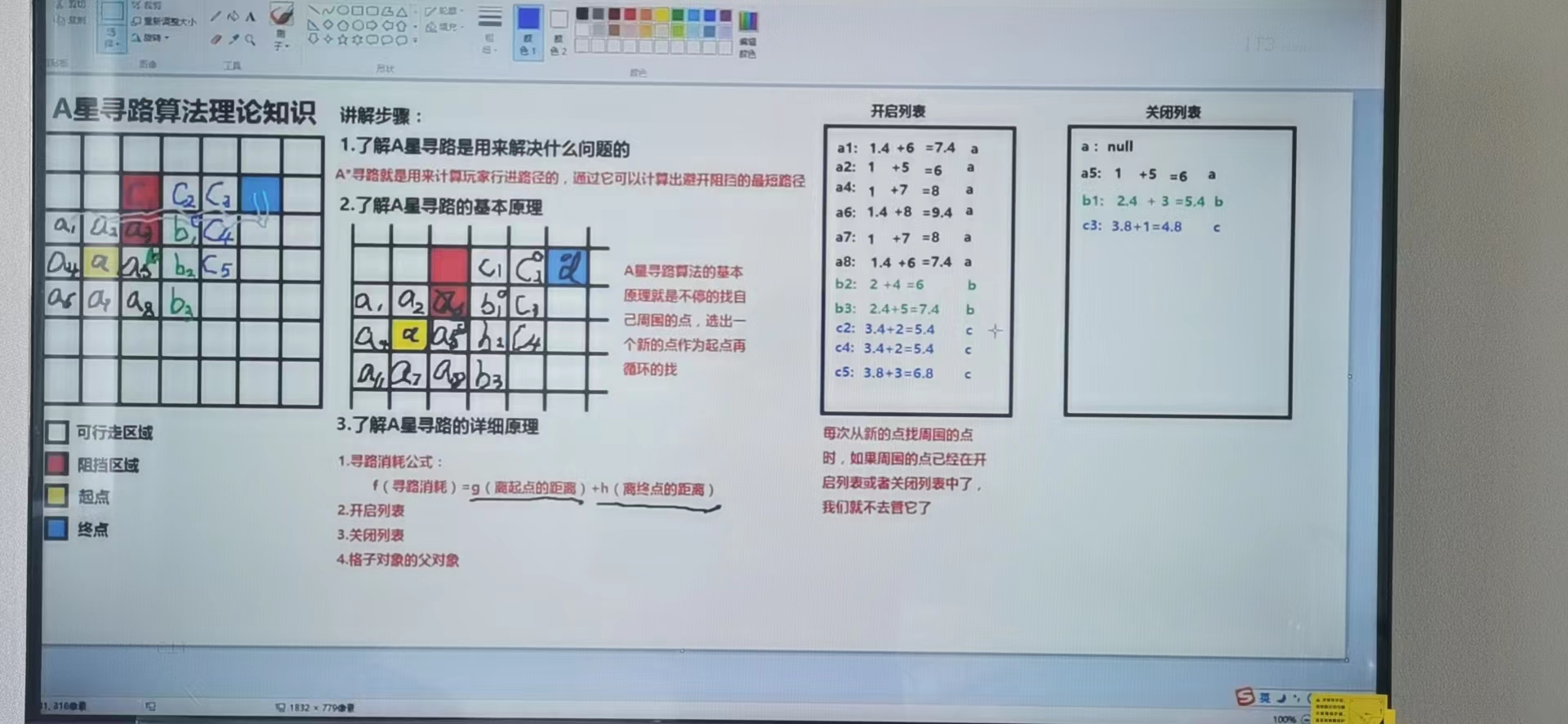
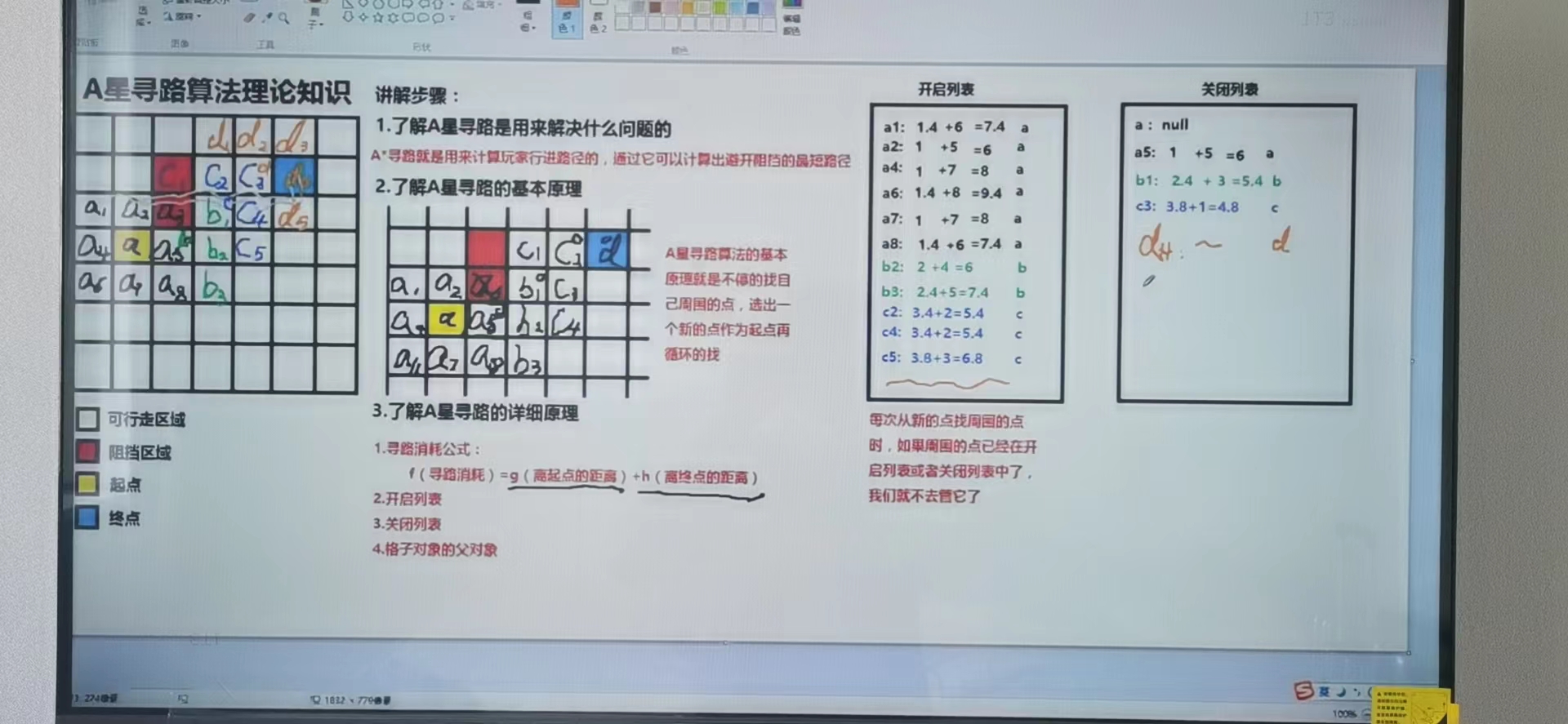
通过例子解析步骤：

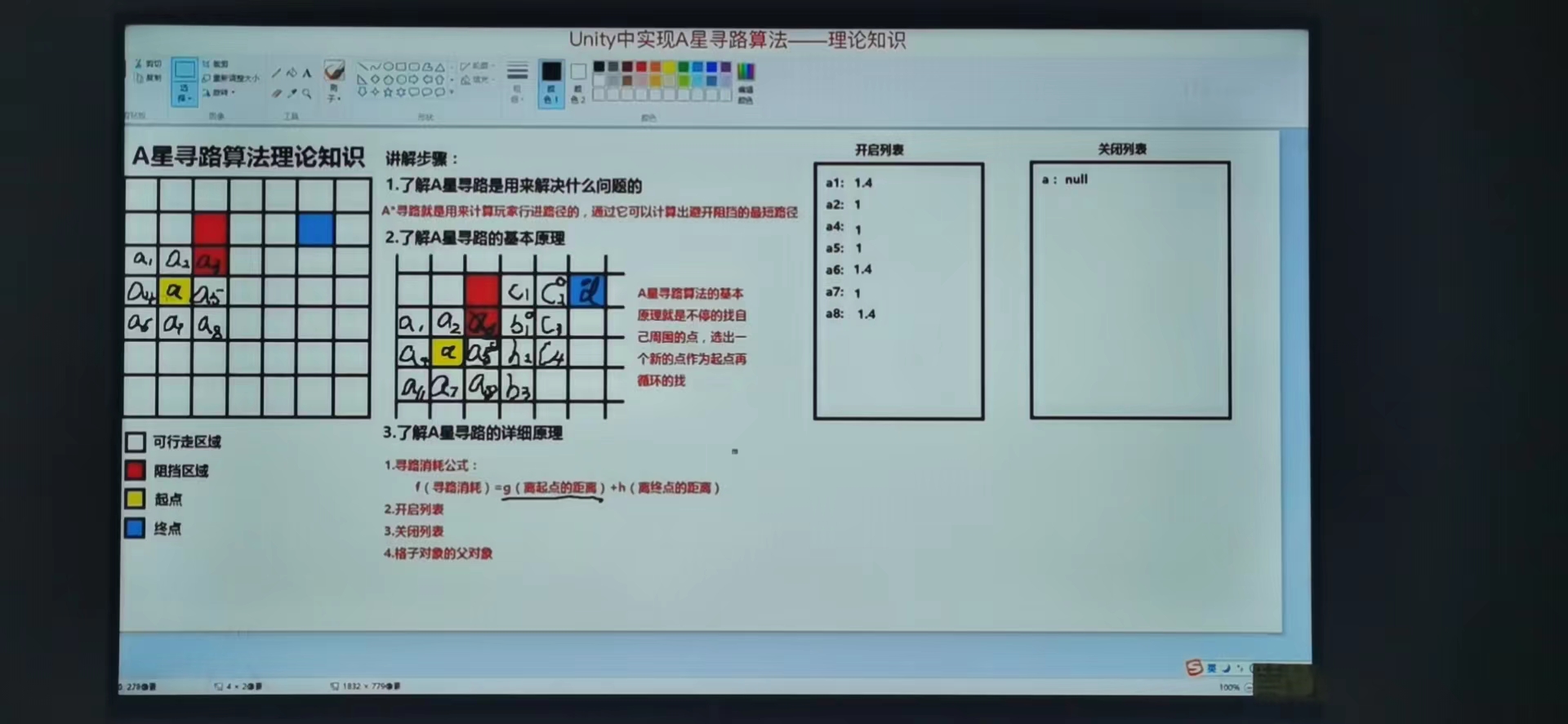
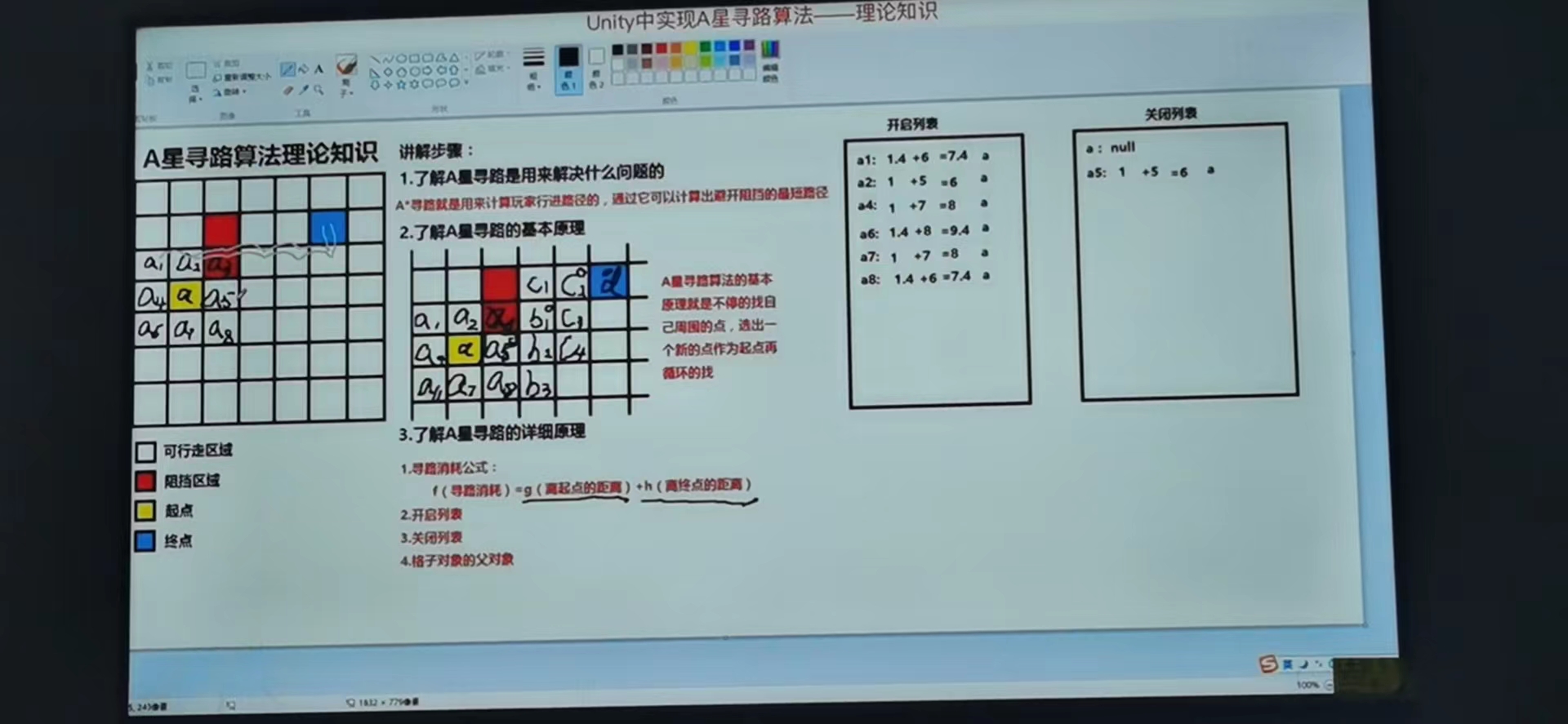
　　1、寻路开始时将起点放入关闭列表中。a:null(父节点为空)，将a的周围的点放入开启列表中例如(a1:a,a2:a,a4:a,a5:a,a6:a,a7:a,a8:a)，并记录他们的父对象为a

　　2、计算开启列表中到a的距离（g）（a1:a:1.4,a2:a:1,a4:a:1,a5:a:1,a6:a:1.4,a7:a:1,a8:a:1.4）

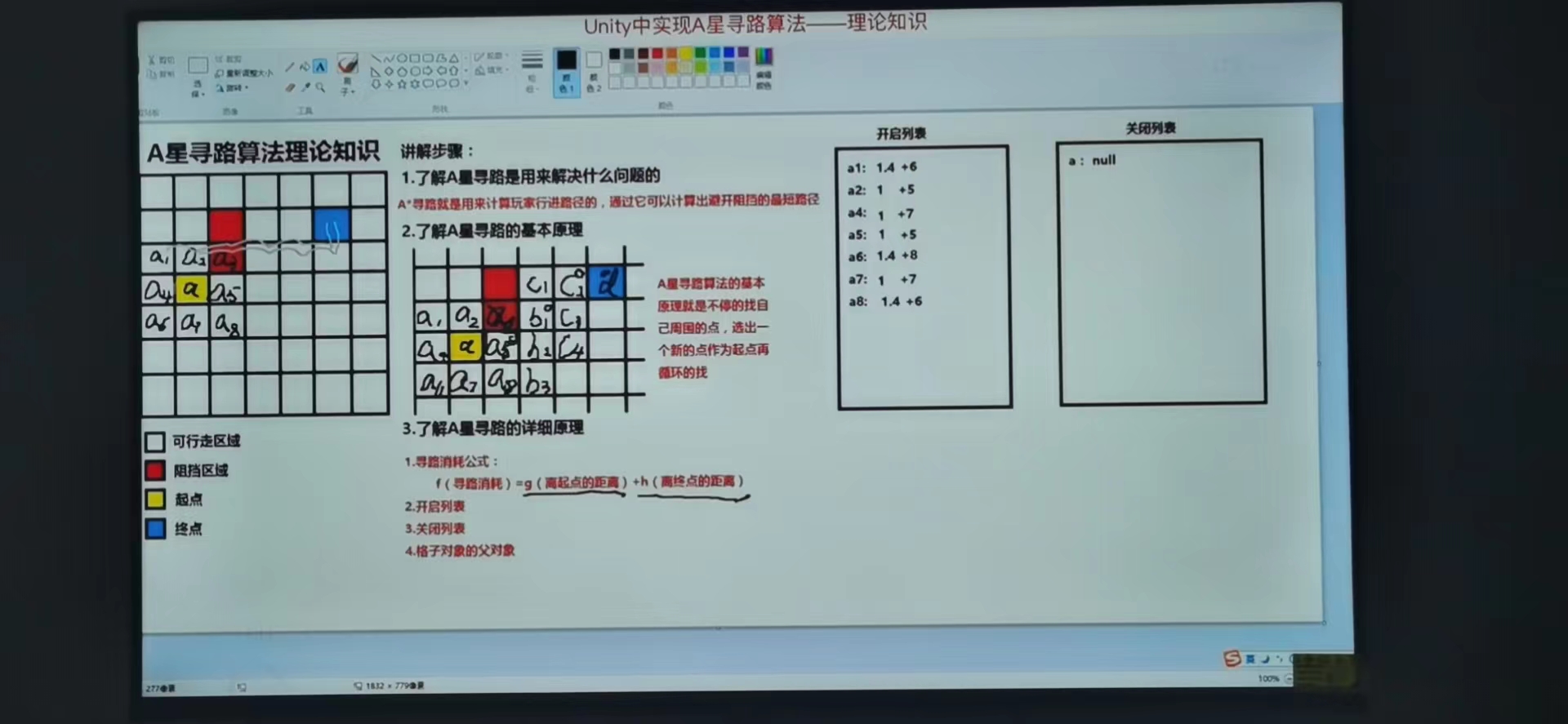
　　3、计算开启列表中到终点的距离(h)，初学的时候就用曼哈顿街区算法(利用横纵（x,y）的格子计算点到终点要走多少了格子）

　　　　（a1:a:1.4 + 6,a2:a:1 + 5,a4:a:1+7,a5:a:1 + 5,a6:a:1.4 + 8,a7:1 + 7 ,a8:a:1.4 + 6）

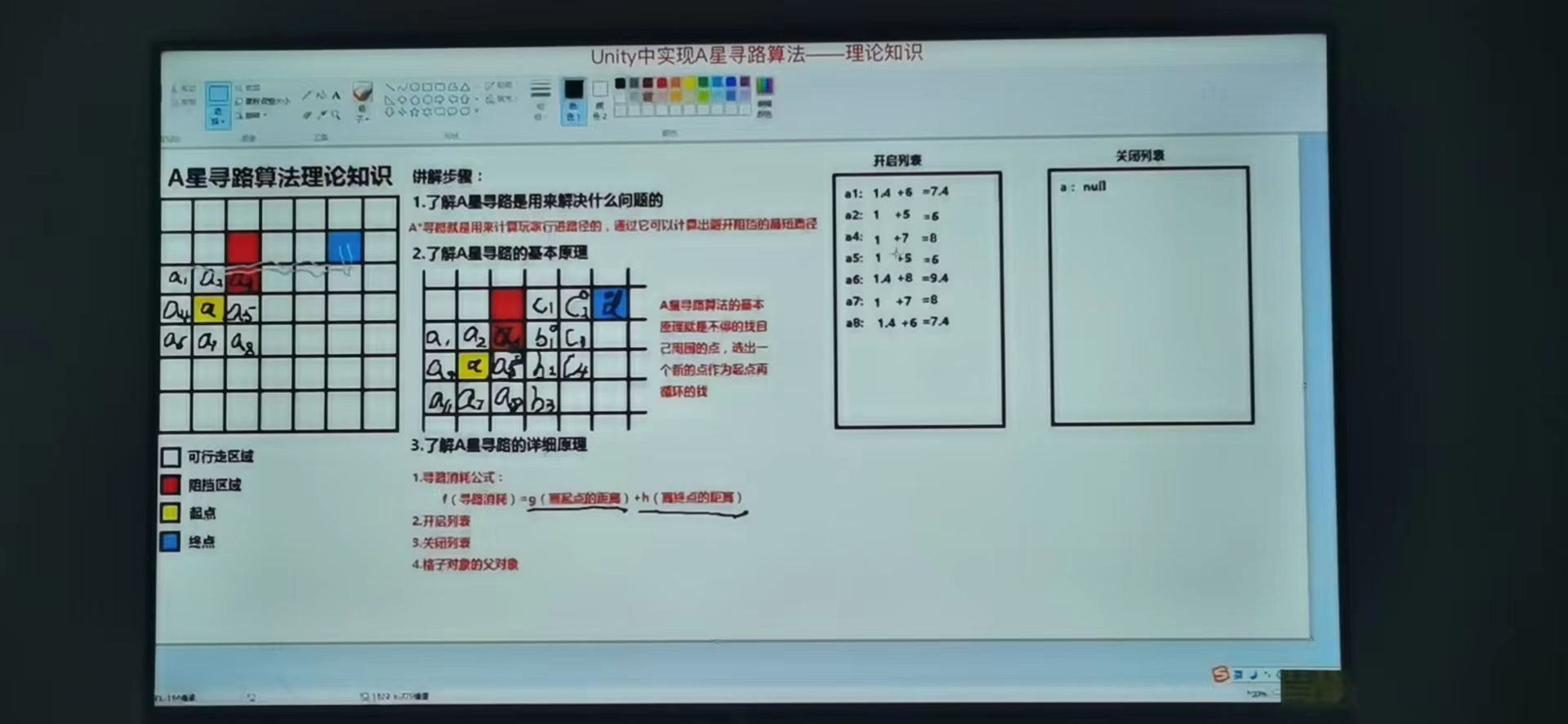
　　4、计算出开启列表中各个点的f值：

　　　　（a1:a:1.4 + 6=7.4,a2:a:1 + 5=6,a4:a:1+7=8,a5:a:1 + 5=6,a6:a:1.4 + 8=9.4,a7:1 + 7=8 ,a8:a:1.4 + 6=7）

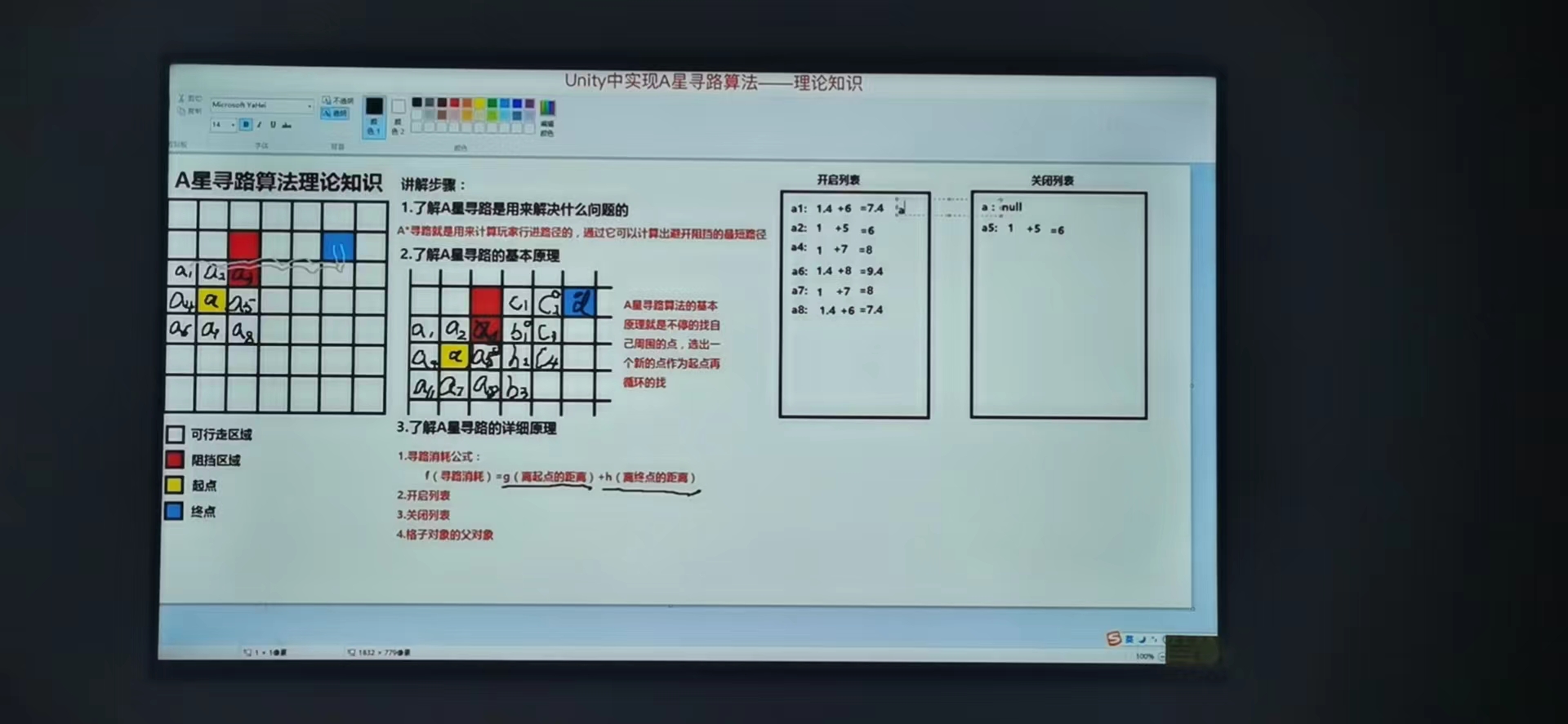
　　5、找出开启列表中f值最小的点，将它从开启列表中移入关闭列表中并将其作为新的起点(a5:a:1+5=6)

 　  6、给a5起个别名b，进入下一个循环

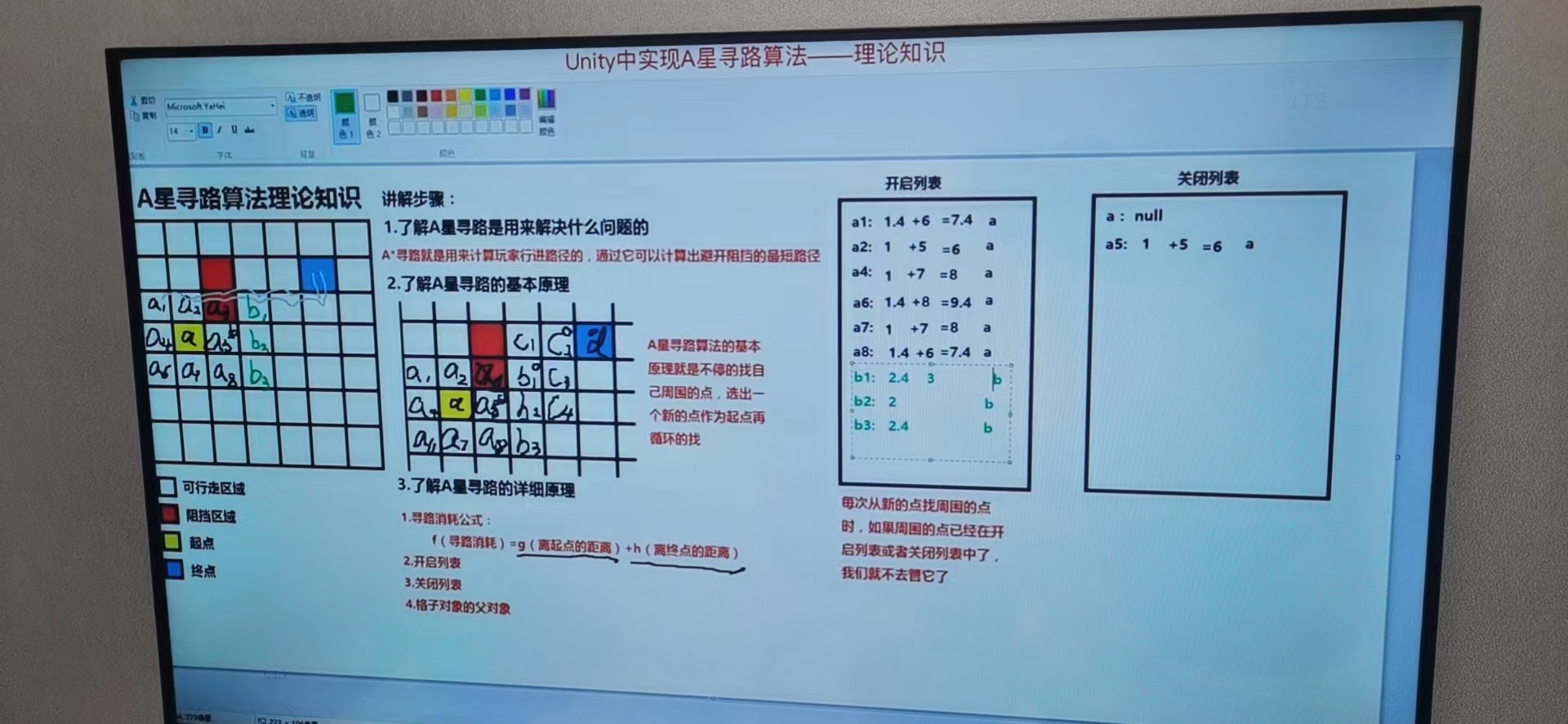
　　注意：每次从新的点找周围的点时，如果周围的点已经在开启列表或者关闭列表中了，我们就不去管它了。

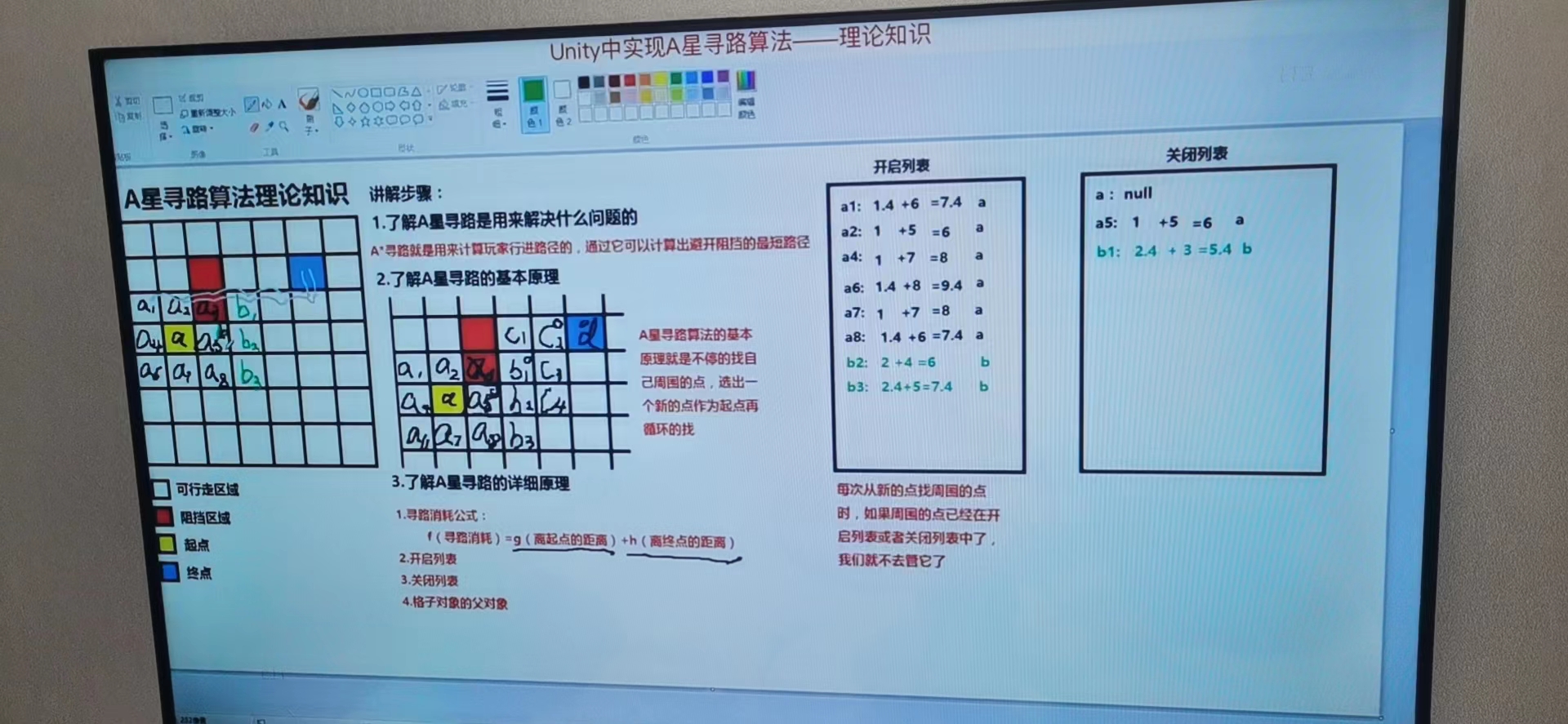
　　7、将b周围的点放入开启列表中,并计算 g(到起点的距离：父节点到起点距离+到父节点的距离)，h(到终点的距离) ,f 　　(b1:b:2.4+3=5.4,b2:b:2+4=6,b3:b:2.4+5=7.4)

　　8、开启列表中所有元素排序找到最小的值b1将它移到关闭列表中去

　　9、将b1取个别名叫c，进入下一个循环

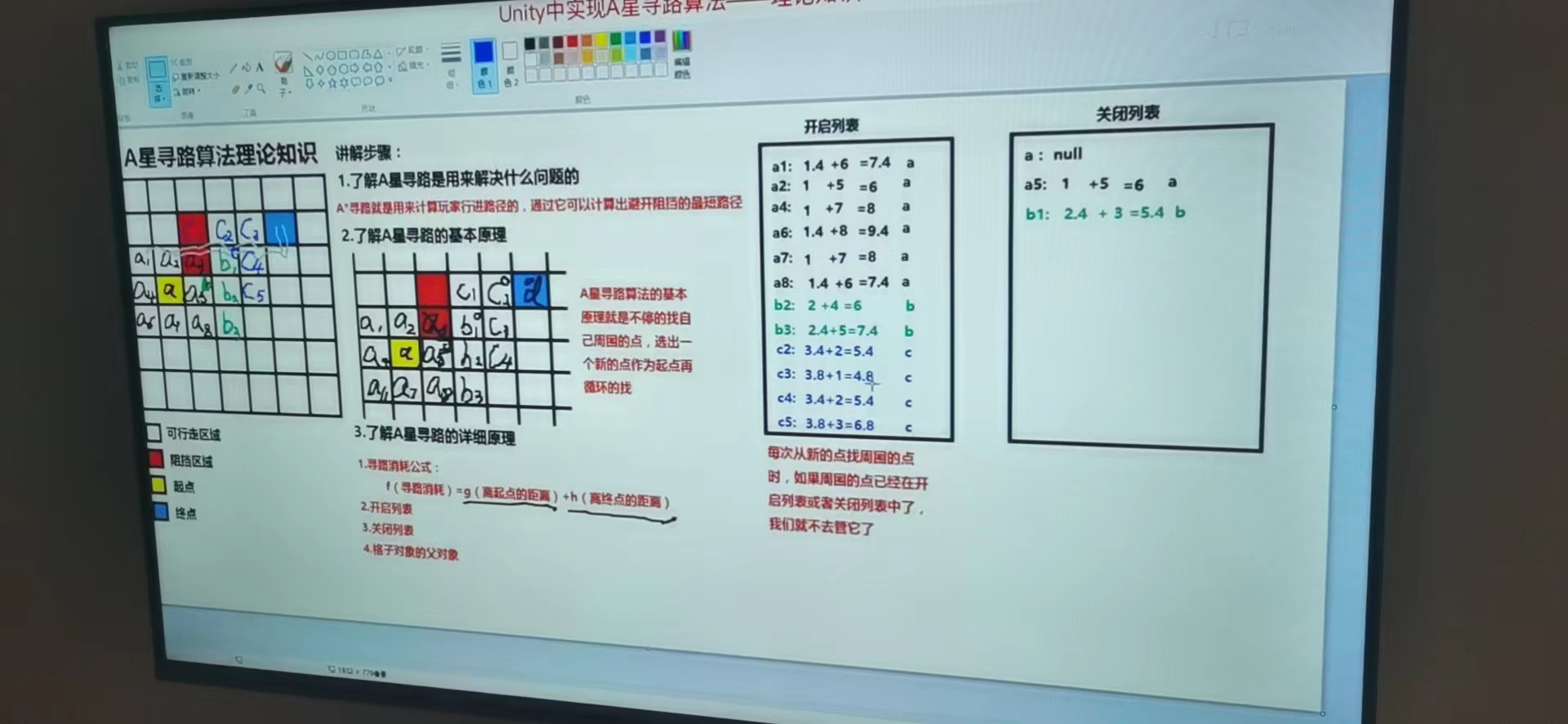
　　10、将c周围的点放入开启列表中，并 g(到起点的距离：父节点到起点距离+到父节点的距离)，h(到终点的距离) ,f

　　　　（c2:c:3.4+2=5.4,c3:c:3.8+1=4.8,c4:c:3.4+2=5.4,c5:c:3.8+3=6.8）

　　11、在开启列表中找到f最小的值c3将其移入关闭列表中

　　12、将c3取个别名d进入下一个循环,计算出f并排序开启列表中得所有得值获取最小值d4,放入关闭列表中，d4是终点寻路结束。

　　　　（d1:d:3.8+3=6.8,d2:d:3.8+2=5.8,d3:d:3.8+1=4.8,d4:d:3.8+0=3.8,d5:3.8+1=4.8）

　　13、在关闭中从终点开始找父对象知道找到点没有父对象就是起点从而得到路径列表。

 注意：

　　1、每次往关闭列表中放点时，我们都应该判断这个点是不是和终点一样，如果一样证明路径找完了，如果不一样继续找。

　　2、路径不是关闭列表中从前往后的移入顺序，因为由于阻挡等原因会移入无用的点所以路径的获取应该从终点找他的父节点，再找父节点直到找到起点，得到的点就是真正的路径（回溯方式找到最终路径）

思考：如何判断是一条死路

　　死路判断: 开启列表为空都还没有找到终点就认为是死路

整个例子图示如下：