推荐模型PNN: 原理介绍与TensorFlow2.0实现

1. 简介

学习用户响应在信息检索领域有非常重要的应用，但是这些领域中有大量的类别特征，每个大类叫做一个域即field（城市域，性别域，id域等）。这些不同域之间的特征模式的表示不能简单的采用onehot，一方面是过拟合，数据过于稀疏，另一方面也是会带来参数量巨大的问题。

所以，乘积网络——Product-based Neural Network，PNN是一个基于神经网络的推荐模型，主要的改进和创新点在于乘积层的应用。乘积层的内积和外积操作能很大程度上增加多类别特征的（高阶）交叉能力，这是传统模型LR， FM以及GBDT所不能及的。

目前已有模型的局限性：FNN模型（矩阵分解机的神经网络）初始化采用了预训练的FM数据，CCPM（基于卷积的预测模型）卷积操作只能观察相邻特征的关系，不能观察非邻域特征的交叉模式。而PNN模型技能学习局部特征，也能学习高阶交叉模式。

在特征交叉的相关模型中FM, FFM都证明了特征交叉的重要性，FNN将神经网络的高阶隐式交叉加到了FM的二阶特征交叉上，一定程度上说明了DNN做特征交叉的有效性。但是对于DNN这种“add”操作的特征交叉并不能充分挖掘类别特征的交叉效果。PNN虽然也用了DNN来对特征进行交叉组合，但是并不是直接将低阶特征放入DNN中，而是设计了Product层先对低阶特征进行充分的交叉组合之后再送入到DNN中去。

其中，PNN以乘积层是内积还是外积分为IPNN，和OPNN（I是inner，O是outer）。

2. 模型原理

模型结构图

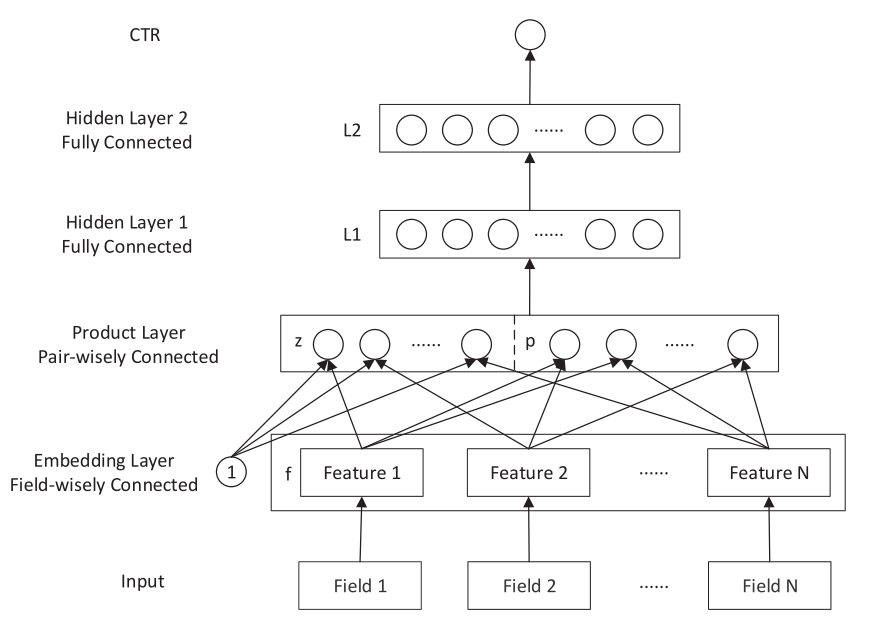
image

从模型上看，CTR，L2， L1以及Embedding层都是常规层。

  • CTR部分就是目标函数为0-1损失函数logloss，激活函数为sigmoid。\(\hat y = \sigma(W_3l_2+b_3)\)

  • L2层为ReLu激活函数的层。\(l_2=ReLu(W_2l_1+b_2)\)

  • L1层为\(l_1 = ReLu(l_z + l_p + b1)\).

  • 这个模型创新部分就在于product layer 的设计。product分为线性部分和非线性部分\(z,p\)，下面详细介绍(不懂的部分可以结合代码部分一起看)。

1. 线性部分

一阶特征(未经过显式特征交叉处理)，对应论文中的\(l_z=(l_z^1,l_z^2, ..., l_z^{D_1})\)。（D1为L1的神经元数量）

\(l_z\)所求就是\(l_z^n\)矩阵内积（形状相同的矩阵对应位置元素，对应相乘再相加得到一个标量）,排列为D1列。代码实现可以Flatten。

\[l_z=(l_z^1,l_z^2, ..., l_z^{D_1})\\ z = (z_1, z_2, ..., z_N) \\ l_z^n = W_z^n \odot{z} \\ l_z^n = W_z^n \odot{z} = \sum_{i=1}^N \sum_{j=1}^M (W_z^n)_{i,j}z_{i,j} \]

总之，用D1个W权重矩阵与N个向量长度为M的EmbeddingVector相乘得到的D1个数字作为线性部分的结果\(l_z\)。

2. 非线性部分

整体上看，\(l_p\)的计算为D1个\(l_p^n\)排列而成的矩阵，具体为，

\[l_p=(l_p^1,l_p^2, ..., l_p^{D_1}) \\ l_p^n = W_p^n \odot{p} \\ p = \{p_{i,j}\}, i=1,2,...,N,j=1,2,...,N \]

求\(p\)分为两种方式：内积和外积。

2.1 IPNN

使用内积计算特征交叉，类似于FM（向量两两内积）即，

\[g(f_i,f_j) = <f_i, f_j> \]

代入\(l_p^n\)得到，

\[\begin{align} l_p^n &= W_p^n \odot{p} \\ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n)_{i,j}p_{i,j} \\ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n)_{i,j}<f_i, f_j> \end{align} \]

总的到L1层所需要的复杂度为：

时间复杂度解释：\(p_{ij}\)其实是一个数，得到一个\(p_{ij}\)的时间复杂度为M，p的大小为\(NN\)，因此计算得到p的时间复杂度为\(NNM\)。而再由p得到\(l_p\)的时间复杂度是\(N*N*D_1\)。因此 对于IPNN来说，总的时间复杂度为\(N*N(D_1+M)\)。

空间复杂度解释：也就是参数的数量\(D_1*(NN+MN)=D_1N(M+N)\)

由于N是比较大的需要简化：

计算的内积矩阵\(p\)是对称的，那么与其对应元素做矩阵内积的矩阵\(W_p^n\)也是对称的，对于可学习的权重来说如果是对称的是不是可以只使用其中的一半就行了呢，

所以基于这个思考，对Inner Product的权重定义及内积计算进行优化，首先将权重矩阵分解\(W_p^n=\theta^n \theta^{nT}\),此时\(\theta^n \in R^N\)（参数从原来的\(N^2\)变成了\(N\)）,将分解后的\(W_p^n\)带入\(l_p^n\)的计算公式有：

\[\begin{align} l_p^n &= W_p^n \odot{p} \\ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n)_{i,j}p_{i,j} \\ &= \sum_{i=1}^N \sum_{j=1}^N \theta^n \theta^n <f_i, f_j> \\ &= \sum_{i=1}^N \sum_{j=1}^N <\theta^n f_i, \theta^n f_j> \\ &= <\sum_{i=1}^N \theta^n f_i, \sum_{j=1}^N \theta^n f_j> \\ &= ||\sum_{i=1}^N \theta^n f_i||^2 \end{align} \]

所以优化后的\(l_p\)的计算公式为：

\[l_p = (||\sum_{i=1}^N \theta^1 f_i||^2, ||\sum_{i=1}^N \theta^2 f_i||^2, ..., ||\sum_{i=1}^N \theta^{D_1} f_i||^2) \]

其中，\(\theta\)是一个标量 ，每一个\(l_p^n\)需要计算MN次（N个特征类别，每个特征有M维度）变成数字，共有D1个，所以复杂度均降为\(D_1MN\)。

2.2 OPNN

使用向量的外积来计算矩阵\(p\),首先定义向量的外积计算

\[g(i,j) = f_i f_j^T \]

从外积公式可以发现两个向量的外积得到的是一个矩阵，与上面介绍的内积计算不太相同，内积得到的是一个数值。内积实现的Product层是将计算得到的内积矩阵，乘以一个与其大小一样的权重矩阵，然后求和，按照这个思路的话，通过外积得到的\(p\)计算\(W_p^n \odot{p}\)相当于之前的内积值乘以权重矩阵对应位置的值求和就变成了，外积矩阵乘以权重矩阵中对应位置的子矩阵然后将整个相乘得到的大矩阵对应元素相加，用公式表示如下：

\[\begin{align} l_p^n &= W_p^n \odot{p} \\ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n)_{i,j}p_{i,j} \\ &= \sum_{i=1}^N \sum_{j=1}^N (W_p^n)_{i,j} f_i f_j^T \end{align} \]

需要注意的是此时的\((W_p^n)_{i,j}\)表示的是一个矩阵，而不是一个值，此时计算\(l_p\)的复杂度是\(O(D_1*N^2*M^2)\), 其中\(N^2\)表示的是特征的组合数量，\(M^2\)表示的是计算外积的复杂度。这样的复杂度肯定是无法接受的，所以为了优化复杂度，PNN的作者重新定义了\(p\)的计算方式：

\[p=\sum_{i=1}^N \sum_{j=1}^N f_i f_j^T = f_{\sum}(f_\sum)^T\\ f_\sum = \sum_{i=1}^N f_i \]

相当于先将原来的embedding向量在特征维度上先求和，变成一个向量之后再计算外积(相当于池化操作，抹平了不同特征的异化，其实会增加不准确度)。

若原embedding向量表示为\(E \in R^{N\times M}\)，其中\(N\)表示特征的数量，M表示的是所有特征的总维度，即\(N*emb\_dim\),。在特征维度上进行求和就是将\(E \in R^{N\times M}\)矩阵压缩成了\(E \in R^M\), 然后两个\(M\)维的向量计算外积得到最终所有特征的外积交叉结果\(p\in R^{M\times M}\)，最终的\(l_p^n\)可以表示为：

\[l_p^n = W_p^n \odot{p} = \sum_{i=1}^N \sum_{j=1}^N (W_p^n)_{i,j}p_{i,j} \\ \]

最终的计算方式和\(l_z\)的计算方式看起来差不多，但是需要注意外积优化后的\(W_p^n\)的维度是\(R^{M \times M}\)的，\(M\)表示的是特征矩阵的维度，即\(N*emb\_dim\)。

虽然叠加概念的引入可以降低计算开销，但是中间的精度损失也是很大的，性能与精度之间的tradeoff

3.代码实现

Product层需要自定义实现，其他部分可以借用TensorFlow的API实现。

3.1 乘积层

lz线性部分的实现是由D1个权重矩阵分别与特征矩阵（权重矩阵和特征矩阵同维度为N*M,N 为特征个数，M为embedding维度）点积得到的D1个标量，然后把这个D1个标量连接在一起构成一个向量。

代码部分简化为：直接将权重维度设置为(N*M, D1)，则不需要循环D1次分别做点积，而是两个矩阵的直接做矩阵乘法得到D1维度的向量：

# 先将所有的embedding拼接起来计算线性信号部分的输出
concat_embed = Concatenate(axis=1)(inputs) # B x feat_nums x embed_dims
# 将两个矩阵都拉成二维的，然后通过矩阵相乘得到最终的结果
concat_embed_ = tf.reshape(concat_embed, shape=[-1, self.feat_nums * self.embed_dims])
lz = tf.matmul(concat_embed_, self.linear_w) # B x units

lp非线性部分

首先要理解的是lp是由D1个标量组成的D1维向量，每次非线性操作都将得到D1向量的一个元素，即标量

这部分包含两个内积和外积，分别介绍。

1. 内积

内积的原理已经说明清楚，这里再提一点，lp向量的每一个维度的元素所求为N*N维度的点积，所以论文简化了这个操作，直接降低为N维度的点积，即为每个特征（总共为N*M每个维度为1*M）乘以一个权重数字，所以权重维度为N*1，具体展开如下图，

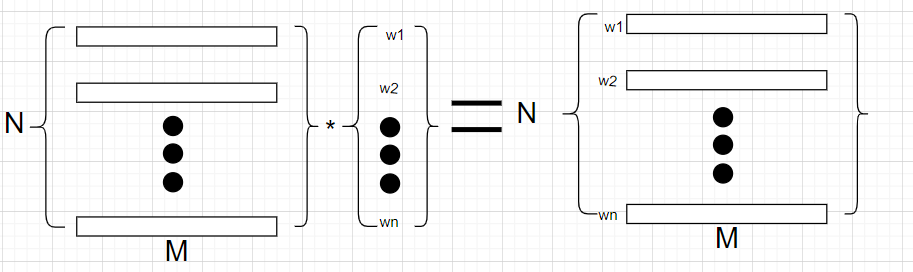
image

然后基于特征维度压缩求和，得到M*1的向量即论文中的\(\delta^n_i\),最终平方求和得到一个标量数字。

delta = tf.multiply(concat_embed, tf.expand_dims(self.inner_w[i], axis=1)) # B x feat_nums x embed_dims
# 在特征之间的维度上求和
delta = tf.reduce_sum(delta, axis=1) # B x embed_dims
# 最终在特征embedding维度上求二范数得到p
lpi = tf.reduce_sum(tf.square(delta), axis=1, keepdims=True) # B x 1

重复D1次, 得到D1个维度的向量。

2. 外积

外积同样做了简化。

首先将向量沿着特征维度进行求和（类似于不同类型 特征做池化（平均池化，求和池化））。

tf.reduce_sum(N*M的特征矩阵, axis=1)

然后对简化之后的特征做矩阵乘法（即外积运算）, 类似论文中的fi和fj。

tf.matmul(f1, f2) # B * embed_dims * embed_dims

最后对外积结果添加权重求和得到一个数字。

理解了内积部分，同样很容易理解外积部分。主要是对权重的把握 以及如何得到一个标量。

具体代码部分为：

初始化：glorot_normal
* 各个层的激活值h（输出值）的方差要保持一致
* 各个层对状态Z的梯度的方差要保持一致
参见：https://blog.csdn.net/qq_27825451/article/details/88707423

class ProductLayer(keras.layers.Layer):
    def __init__(self, units, use_inner=True, use_outer=False, **kwargs):
        super(ProductLayer, self).__init__(**kwargs)
        self.units = units # 论文中D1
        self.use_inner = use_inner
        self.use_outer = use_outer

    #build在执行call函数时执行一次，获得输入的形状；
    #定义输入X时为列表，每个元素为一个类别的Embeding所以，每个元素的形状为(batch_size, 1, emb_dim)，因此没有被flatten
    def build(self, input_shape):
        self.feat_nums = len(input_shape) # 列表长度为所有类别
        self.embed_dims = input_shape[0].as_list()[-1] # (batch_size, 1, emb_dim)
        flatten_dims = self.feat_nums * self.embed_dims
        
        self.linear_w = self.add_weight(name='linear_w', shape=(flatten_dims, self.units), initializer='glorot_normal')

        if self.use_inner:
            # 优化之后的内积权重是未优化时的一个分解矩阵，未优化时的矩阵大小为：D x N x N 
            # 优化后的内积权重大小为：D x N
            self.inner_w = self.add_weight(name='inner_w', shape=(self.units, self.feat_nums), initializer='glorot_normal')
        if self.use_outer:
            # 优化为 每个向量矩阵 外积权重大小为：D x M x M
            self.outer_w = self.add_weight(name='outer_w', shape=(self.units, self.embed_dims, self.embed_dims), initializer='glorot_normal')

    def call(self, inputs):
        concat_emb = tf.concat(inputs, axis=1) # B* feat_nums*emb_dim
        # lz
        _concat_emb = tf.reshape(concat_emb, shape=[-1, self.feat_nums*self.embed_dims])
        lz = tf.matmul(_concat_emb, self.linear_w) # B * D1

        #lp: 一个元素一个元素的计算
        lp_list = []
        #inner： 每个元素都是内积成权重的结果
        if self.use_inner:
            for i in range(self.units):
                # self.inner_w[i] : (embed_dims, ) 添加一个维度变成 (embed_dims, 1)
                lpi = tf.multiply(concat_emb, tf.expand_dims(self.inner_w[i], axis=1)) # 论文的delta:B * feat_nums* emb_dims
                # 求范数：先求和再开方
                lpi = tf.reduce_sum(lpi, axis=1) # B * emb_dims
                lpi = tf.square(lpi) # B * emb_dims A Tensor. Has the same type as x.
                lpi = tf.reduce_sum(lpi, axis=1, keepdims=True) # B * 1 这里没有再次进行开方，因为不影响结果, 必须要有keepdims=True参数否则维度变成B
                lp_list.append(lpi)
        #outer: 每个元素都是 特征维度求和的外积 乘以权重
        if self.use_outer:
            feat_sum = tf.reduce_sum(concat_emb, axis=1) # B*emb_dims
            # 为了求外积，构造转置向量
            f1 = tf.expand_dims(feat_sum, axis=1) # B* 1* emb_dims
            f2 = tf.expand_dims(feat_sum, axis=2) # B* emb_dims * 1
            # 外积
            product = tf.matmul(f2, f1) # B * emb_dims * emb_dims
            for in range(self.units):
                # self.outer_w[i] 为emb_dims * emb_dims不必增添维度
                lpi = tf.multiply(product, self.outer_w[i]) # B * emb_dims * emb_dims
                # 求和
                lpi = tf.reduce_sum(lpi, axis=[1,2]) # 把emb_dims压缩下去 (B,)
                # 没法连接
                lpi = tf.expand_dims(lpi, axis=1) # B * 1
                lp_list.append(lpi)
        lp = tf.concat(lp_list, axis=1)

        product_out = tf.concat([lz, lp], axis=1)
        return product_out

3.2 PNN实现

除了乘积层之外没有特别的部分，因此，不再进行Embedding的和类的封装，而是通过Keras的Input做前向传播的运算得到模型的输出。

具体看代码部分的注释：

设置特征类型：SparseFeat和DenseFeat

from collections import namedtuple
SparseFeat = namedtuple('SparseFeat', ['name', 'vocabulary_size', 'embedding_size'])
DenseFeat = namedtuple('DenseFeat', ['name', 'dimension'])

构造Input字典，然后通过字典key得到对应的数据

# 构建Input字典：每个输入特征构成一个Input，方便对不同的特征输入
def build_input_layers(feat_cols):
    """
    feat_cols是列表，每个元素都是namedtuple表征是否是稀疏向量
    return： 稠密和稀疏两个字典
    """
    sparse_dict, dense_dict = dict(), dict()
    
    for fc in feat_cols:
        if isinstance(fc, DenseFeat):
            dense_dict[fc.name] = keras.Input(shape=(1, ), name=fc.name)
        if isinstance(fc, SparseFeat):
            sparse_dict[fc.name] = keras.Input(shape=(1, ), name=fc.name)
    return dense_dict, sparse_dict

构建emb层和输出列表

def build_emb_layers(feat_cols):
    """
    返回emb字典
    """ 
    emb_dict = {}
    #使用python内建函数，filter过滤出稀疏特征来进行Embedding
    sparse_feat = list(filter(lambda fc: isinstance(fc, SparseFeat), feat_cols)) if feat_cols else []
    for fc in sparse_feat:
        emb_dict[fc.name] = keras.layers.Embedding(input_dim=fc.vocabulary_size+1,
                                                   output_dim=fc.embedding_size,
                                                   name='emb_' + fc.name)
    return emb_dict


def concat_emb_layers(feat_cols, input_layer_dict, emb_layer_dict, flattern=False) :
    """
    将输入层 经过emb层得到最终的输出
    """
    sparse_feat = list(filter(isinstance(lambda fc: fc, SparseFeat), feat_cols)) if feat_cols else []
    emb_list = []
    for fc in sparse_feat:
        _input = input_layer_dict[fc.name] # 1 * None
        _emb = emb_layer_dict[fc.name] # B*1*emb_dim
        embed = _emb(_input)

        if flattern:
            embed = keras.layers.Flatten()(embed)
        emb_list.append(embed)
    
    return emb_list

最后的MLP和打分层

def get_dnn_logit(dnn_inputs, units=(64, 32)):
    """
    MLP的部分，以及最终的评分函数
    """
    dnn_out = dnn_inputs
    for unit in units:
        dnn_out = keras.layers.Dense(unit, activation='relu')(dnn_out) # 不需要指定input_shape，Input里已经有了

    logit = keras.layers.Dense(1, activation='sigmoid')(dnn_out)

    return logit

PNN模型

def PNN(feat_cols, dnn_units=(64, 32), D1=32, inner=True, outer=False) :
    dense_input_dict, sparse_input_dict = build_input_layers(feat_cols)
    #Model的参数中 inputs是列表 和outputs
    input_layers = list(sparse_input_dict.values())

    # 前向过程
    emb_dict = build_emb_layers(feat_cols)
    emb_list = concat_emb_layers(feat_cols,sparse_input_dict, emb_dict, flattern=True) # 测试True的效果
    dnn_inputs = ProductLayer(units=D1, use_inner=inner, use_outer=outer)(emb_list)
    output_layer = get_dnn_logit(dnn_inputs, units=dnn_units)

    model = keras.layers.Model(input_layers, output_layer)
    return model

3.3 经过数据criteo_sample测试结果

def data_process(data_df, dense_features, sparse_features):
    data_df[dense_features] = data_df[dense_features].fillna(0.0)
    for f in dense_features:
        data_df[f] = data_df[f].apply(lambda x: np.log(x+1) if x > -1 else -1)
        
    data_df[sparse_features] = data_df[sparse_features].fillna("-1")
    for f in sparse_features:
        lbe = LabelEncoder()
        data_df[f] = lbe.fit_transform(data_df[f])
    
    return data_df[dense_features + sparse_features + ['label']]


path = 'criteo_sample.txt'
data = pd.read_csv(path)
columns = data.columns.values() # ndarray
dense_feats = [feat for feat in columns if 'I' in feat]
sparse_feats = [feat for feat in columns if 'C' in feat]
# 数据处理
train_data = data_process(data, dense_feats, sparse_feats)
#传入类别特征
dnn_feat_cols = [SparseFeat(feat, vocabulary_size=data[feat].nunique(), embedding_size=4) for feat insparse_feats]
# 构建模型
history = PNN(dnn_feat_cols)
history.compile(optimizer="adam", loss="binary_crossentropy", metrics=['auc', 'binary_crossentropy'])
train_inputs = {name: data[name] for name in dense_feats+sparse_feats}
history.fit(train_inputs, train_data['label'].values,
    batch_size=64, epochs=5, validation_split=0.2, )

得到：

val_binary_crossentropy: 0.6666 - val_auc: 0.5912
Epoch 4/5
160/160 [==============================] - 0s 592us/sample - loss: 0.6411 - binary_crossentropy: 0.6411 - auc: 0.6830 - val_loss: 0.6575 - val_binary_crossentropy: 0.6575 - val_auc: 0.5926
Epoch 5/5
160/160 [==============================] - 0s 586us/sample - loss: 0.6214 - binary_crossentropy: 0.6214 - auc: 0.7478 - val_loss: 0.6479 - val_binary_crossentropy: 0.6479 - val_auc: 0.5755

4. 小结

本篇文章的主要目的是对于信息检索领域多个类别稀疏特征的处理，由人工特征工程交叉，向复杂特征工程交叉实现，复杂特征工程通过乘积层实现，乘积层是比较难以理解的部分，且计算复杂度是十分巨大的，因此进行了简化。

由于简化尤其是外积，效果可能不会特别好，比如说不同类别所属field不同，进行求和则过度池化。但这是效率和性能权衡的结果。

模型的成功之处是乘积层（内积，外积），相对于MLP网络简单交叉的更加多样化，使得模型更容易捕获交叉信息。局限性在于为了提高效率进行了一系列的简化，可能一定程度上会忽略原始特征向量中的有价值信息。

REF:
ch_blog

https://mp.weixin.qq.com/s/-WEGvWfsJGbWkQS0FbWZhQ

author github

代码参考datawhalechina

  • Product Layer中z中每个圈都是一个向量，向量大小为Embedding Vector大小，向量个数 = Field个数 = Embedding向量的个数。
  • Product Layer中如果是内积，p中每个圈都是一个值；如果是外积，p中每个圆圈都是一个二维矩阵。
posted @ 2021-04-15 23:51  道之有道  阅读(1594)  评论(0)  编辑  收藏  举报