LeetCode101学习笔记-9.9

  • LeetCode默认的树表示方法如下：
1  * struct TreeNode {
2  *     int val;
3  *     TreeNode *left;
4  *     TreeNode *right;
5  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
6  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
7  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
8  * };

 

104. Maximum Depth of Binary Tree

1 class Solution {
2 public:
3     int maxDepth(TreeNode* root) {
4         return root?max(maxDepth(root->left),maxDepth(root->right))+1:0;
5     }
6 };

110. Balanced Binary Tree

 1 class Solution {
 2 public:
 3     bool isBalanced(TreeNode* root) {
 4         if(helper(root) == -1)return false;
 5         return true;
 6     }
 7     int helper(TreeNode* root){
 8         if(!root)return 0;
 9         int l=helper(root->left),r=helper(root->right);
10         if(l==-1 || r==-1 || abs(l-r)>1)return -1;
11         return max(l,r)+1;
12     }
13 };

543. Diameter of Binary Tree

 1 class Solution {
 2 public:
 3     int diameter=0;
 4     int diameterOfBinaryTree(TreeNode* root) {
 5         helper(root);
 6         return diameter;
 7     }
 8     int helper(TreeNode* root){
 9         if(!root)return 0;
10         int l=helper(root->left),r=helper(root->right);
11         diameter=max(l+r,diameter);
12         return max(l,r)+1;
13     }
14 };

437. Path Sum III

 1 class Solution {
 2 public:
 3     int pathSum(TreeNode* root, int targetSum) {
 4         //限定了路径只能从父节点到子节点
 5         if(!root)return 0;
 6         return helper(root,targetSum)+pathSum(root->left,targetSum)+pathSum(root->right,targetSum);
 7     }
 8     int helper(TreeNode* root,int val){
 9         if(!root)return 0;
10         int cnt=root->val==val?1:0;
11         cnt+=helper(root->left,val-root->val);
12         cnt+=helper(root->right,val-root->val);
13         return cnt;
14     }
15 };

101. Symmetric Tree

 1 class Solution {
 2 public:
 3     bool isSymmetric(TreeNode* root) {
 4         return !root || helper(root->left,root->right);
 5     }
 6     bool helper(TreeNode* left,TreeNode* right){
 7         if(!left && !right)return true;
 8         if(!left || !right)return false;
 9         if(left->val != right->val)return false;
10         return helper(left->left,right->right)&&helper(left->right,right->left);
11     }
12 };

 637. Average of Levels in Binary Tree

 1 class Solution {
 2 public:
 3     vector<double> averageOfLevels(TreeNode* root) {
 4         vector<double> ans;
 5         queue<TreeNode*> q;
 6         q.push(root);
 7         while(root&&!q.empty()){
 8             double sum=0;
 9             int cnt=q.size();
10             for(int i=0;i<cnt;i++){
11                 TreeNode* node=q.front();
12                 q.pop();
13                 sum+=node->val;
14                 if(node->left)q.push(node->left); 
15                 if(node->right)q.push(node->right);
16             }
17             ans.push_back(sum/cnt);
18         }
19         return ans;
20     }
21 };

 144. Binary Tree Preorder Traversal

 1 class Solution {
 2 public:
 3     vector<int> preorderTraversal(TreeNode* root) {
 4         //非递归解法
 5         vector<int> ans;
 6         stack<TreeNode*> s;
 7         s.push(root);
 8         while(root&&!s.empty()){
 9             TreeNode* node=s.top();
10             s.pop();
11             ans.push_back(node->val);
12             if(node->right)s.push(node->right);
13             if(node->left)s.push(node->left);
14         }
15         return ans;
16     }
17 };

 

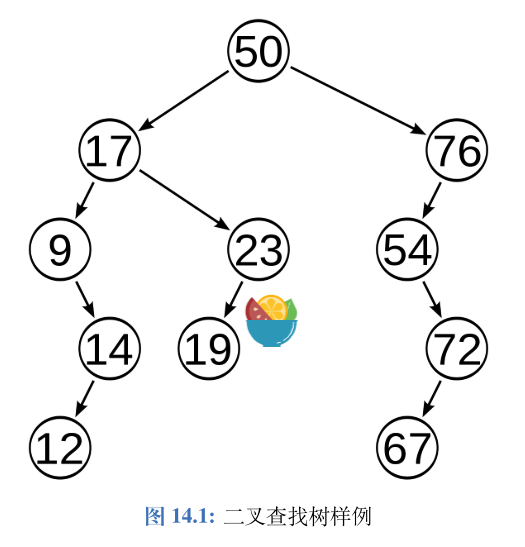
  • 二叉查找树

二叉查找树（Binary Search Tree, BST）是一种特殊的二叉树：对于每个父节点，其左子树中所有节点的值小于等于父结点的值，其右子树中所有节点的值大于等于父结点的值。因此对于一个二叉查找树，我们可以在O(log n) 的时间内查找一个值是否存在。

同时因为二叉查找树是有序的，对其中序遍历的结果即为排好序的数组。

一个二叉查找树的实现如下：

 

 

 

 

 

 

 

 

 

669. Trim a Binary Search Tree

 1 class Solution {
 2 public:
 3     TreeNode* trimBST(TreeNode* root, int low, int high) {
 4         if(!root)return root;
 5         if(root->val > high)return trimBST(root->left,low,high);
 6         if(root->val < low)return trimBST(root->right,low,high);
 7         root->left=trimBST(root->left,low,high);
 8         root->right=trimBST(root->right,low,high);
 9         return root;
10     }
11 };

 

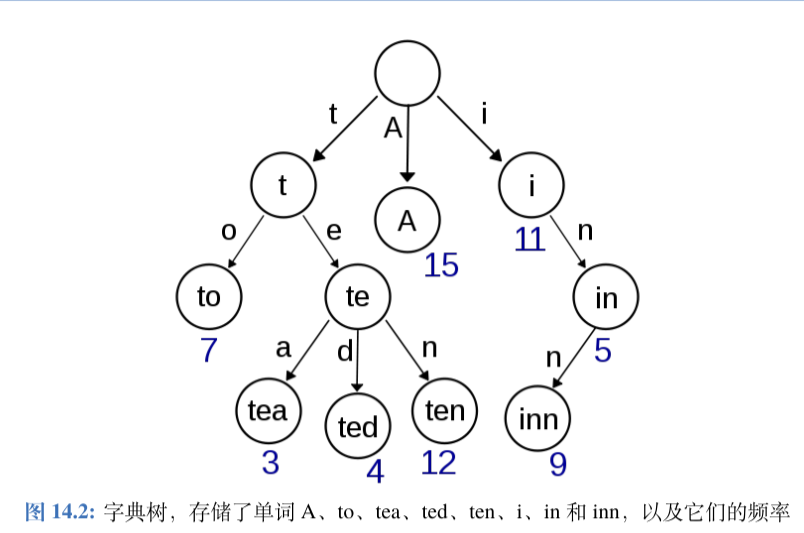
  • 字典树

 

posted @ 2021-09-09 11:15  Rekord  阅读(33)  评论(0)  编辑  收藏  举报