稀疏矩阵

稀疏矩阵就是矩阵中分布着很多零元素（零元素个数远远大于非零元素个数），如果将这个矩阵的每个元素都一一存储，那是很浪费空间的。因此，可以采用一些特殊的存储结构来存储它。有以下几种方法：

1.顺序存储：三元组表示法、伪地址表示法

2.链式存储：邻接表表示法、十字链表表示法

这里介绍三元组表示法。

稀疏矩阵

三元组数据结构为一个长度为n，表内每个元素都有3个分量的线性表，其3个分量分别为值、行下标和列下标。

元素结构体定义如下：

1  typedef struct
2  {
3      int val;
4      int i,j;
5  }Trimat;
6  ​
7  //定义一个含有maxterms个非零元素的稀疏矩阵的三元组
8  Trimat trimat[maxterms+1];//maxterms是已经定义好的常量

 

为了简便起见，可以不使用上述结构体定义，直接申请一个如下的数组即可：

1  int trimat[maxterms+1][3];

 trimat[k] [0]表示原矩阵中的元素按行优先顺序的第k个非零元素的值；trimat[k] [1]和trimat[k] [2]表示第k个元素在矩阵中的位置。规定第0行的3个元素分别用来存储非零元素个数、行数和列数。

 

建立三元组

 1  //A是m*n的稀疏矩阵，B是三元组，maxSize是预先定义好的最大矩阵维数  
 2  void createTrimat(int A[][maxSize],int m,int n,int B[][3])
 3  {
 4      int k=1;//B的行
 5      for(int i=0;i<m;i++)
 6      {
 7          for(int j=0;j<n;j++)
 8          {
 9              if(A[i][j]!=0)//找到非零元素，放入三元组 
10              {
11                  B[k][0]=A[i][j];
12                  B[k][1]=i;
13                  B[k][2]=j;
14                  k++; 
15              }
16          }
17      } 
18      //三元组第一行信息 
19      B[0][0]=k-1;
20      B[0][1]=m;
21      B[0][2]=n;
22  }

 

通过三元组打印矩阵

 1  void print(int B[][3])
 2  {
 3      int k=1;
 4      for(int i=0;i<B[0][1];i++)
 5      {
 6          for(int j=0;j<B[0][2];j++)
 7          {
 8              if(i==B[k][1]&&j==B[k][2])//(i,j)在三元组中 
 9              {
10                  cout<<B[k][0]<<" ";
11                  k++;
12              }
13              else
14                  cout<<"0 ";
15          }
16          cout<<endl;
17      }
18  }

 测试

 1  int main()
 2  {
 3      int A[maxSize][maxSize]={{0,0,0,1},
 4                               {0,0,3,2},
 5                               {1,0,0,0},
 6                               {0,2,0,0}};
 7      int B[maxterms+1][3];
 8      //稀疏矩阵A 转 三元组B 
 9      createTrimat(A,4,4,B);
10      //打印B 
11      for(int i=0;i<6;i++)
12      {
13          for(int j=0;j<3;j++)
14              cout<<B[i][j]<<" ";
15          cout<<endl;
16      }
17      cout<<endl;
18      //由B打印A 
19      print(B);
20       
21      return 0;
22  }

运行

 

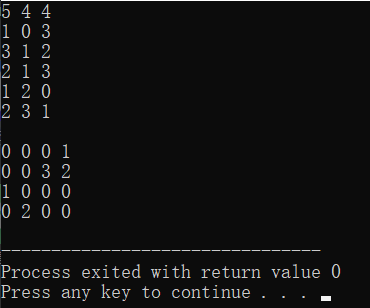
练习

 

1.假设稀疏矩阵A采用三元组表示，编写一个函数，计算其转置矩阵B，要求B也采用三元组表示。

分析：因为三元组内元素是原矩阵按行优先存储的结果，所以不能仅仅将行下标和列下标互换。B中的元素从上往下的顺序是B原矩阵按行从左到右从上到下的顺序，因为转置，B矩阵的第一行是A的第一列，因此正确的做法是找出A的第一列元素，把他们依次放入B的三元组中，然后找A的第二列元素、第三列元素......

 1  void transpose(int A[][3],int B[][3])
 2  {
 3      //更新B的第一行信息 
 4      B[0][0]=A[0][0];
 5      B[0][1]=A[0][2];
 6      B[0][2]=A[0][1];
 7      if(B[0][0]>0)
 8      {
 9          int q=1;//B的行
10          for(int i=0;i<B[0][1];i++) //B的行数 
11          {
12              for(int k=1;k<=B[0][0];k++)
13              {
14                  if(A[k][2]==i)//A的列等于B的行
15                  {
16                      B[q][0]=A[k][0];
17                      B[q][1]=A[k][2];
18                      B[q][2]=A[k][1];
19                      q++;
20                  } 
21              }
22          }
23      }
24  }

 

2.假设稀疏矩阵A和B（两矩阵行列数对应相等）都采用三元组表示，编写一个函数，计算C=A+B，要求C也采用三元组表示，所有矩阵均为int型。

 1  void add(int A[][3],int B[][3],int C[][3])
 2  {
 3      
 4      int i=1,j=1;//i遍历A，j遍历B
 5      int k=1;//C的行 
 6      while(i<=A[0][0]&&j<=B[0][0])
 7      {
 8          if(A[i][1]==B[j][1])//如果A当前元素的行号等于B当前元素的行号，则比较列号 
 9          {
10              if(A[i][2]<B[j][2])//A的列号小于B的列号，则将A这个元素写入C 
11              {
12                  C[k][0]=A[i][0];
13                  C[k][1]=A[i][1];
14                  C[k][2]=A[i][2];
15                  k++;
16                  i++;
17                  
18              }
19              else if(A[i][2]>B[j][2])//A的列号大于B的列号，则将B这个元素写入C 
20              {
21                  C[k][0]=B[j][0];
22                  C[k][1]=B[j][1];
23                  C[k][2]=B[j][2];
24                  k++;
25                  j++;
26              }
27              else //A的列号等于B的列号，则将这两个元素相加，写入C 
28              {
29                  int m=A[i][0]+B[j][0];
30                  if(m!=0)//m有可能为0，不为0才写入C 
31                  {
32                      C[k][0]=m;
33                      C[k][1]=A[i][1];
34                      C[k][2]=A[i][2];
35                      k++;
36                       
37                  } 
38                  i++;
39                  j++;
40              }
41          }
42          else if(A[i][1]<B[j][1])//A当前元素的行号小于B当前元素的行号，则将A的这个元素写入C 
43          {
44              C[k][0]=A[i][0];
45              C[k][1]=A[i][1];
46              C[k][2]=A[i][2];
47              k++;
48              i++;
49          }
50          else //A当前元素的行号大于B当前元素的行号，则将B的这个元素写入C
51          {
52              C[k][0]=B[j][0];
53              C[k][1]=B[j][1];
54              C[k][2]=B[j][2];
55              k++;
56              j++;
57          }
58      }
59          
60          while(i<=A[0][0])//A有剩余元素，B已经处理完毕，将A中元素直接放入C 
61          {
62              C[k][0]=A[i][0];
63              C[k][1]=A[i][1];
64              C[k][2]=A[i][2];
65              k++;
66              i++;     
67     } 
68      
69 while(j<=B[0][0])//B有剩余元素，A已经处理完毕，将B中元素直接放入C  
70     { 
71 C[k][0]=B[j][0]; 
72 C[k][1]=B[j][1]; 
73 C[k][2]=B[j][2]; 
74 k++; 
75 j++; 
76     } 
77      
78 //产生第0行信息  
79 C[0][0]=k-1;  
80 C[0][1]=A[0][1]; 
81 C[0][2]=A[0][2]; 
82 }

 

3.假设稀疏矩阵A和B（分别为m*n和n*k矩阵）采用三元组表示，编写一个函数，计算C=A*B，要求C也是采用三元组表示的稀疏矩阵。

 1  //返回D对应的稀疏矩阵中（i,j）位置上的值 
 2  int getValue(int D[][maxSize],int i,int j)
 3  {
 4      int k=1;
 5      whilt(k<=D[0][0]&&(D[k][1]!=i||D[k][2]!=j))
 6          k++;
 7      if(k<=D[0][0])
 8          return D[k][0];
 9      else 
10          return 0;
11  }
12  //矩阵相乘 
13  void mul(int A[][3],int B[][3],int C[][3],int m,int n,int k)
14  {
15      int p=1;//C的行 
16      for(int i=0;i<m;i++)
17      {
18          for(int j=0;j<k;j++)
19          {
20              for(int l=0;l<n;l++)//A的第m行乘B的第k列 为 C的(m,k)
21                  s+=getValue(A,i,l)+getValue(B,l,j);
22              if(s!=0)
23              {
24                  C[p][0]=s;
25                  C[p][1]=i;
26                  C[p][2]=j;
27                  p++;
28              }
29          }
30      }
31      C[0][0]=p-1;
32      C[0][1]=m;
33      C[0][2]=k; 
34  }

 



posted @ 2021-07-14 16:08  sxkio  阅读(452)  评论(0)  编辑  收藏  举报