AVL树、红黑树以及B树介绍
简介
首先,说一下在数据结构中为什么要引入树这种结构,在我们上篇文章中介绍的数组与链表中,可以发现,数组适合查询这种静态操作(O(1)),不合适删除与插入这种动态操作(O(n)),而链表则是适合删除与插入,而查询效率则就比较慢了,本文要分享学习的树就是为了平衡这种静态操作与动态操作的差距。
一、二叉查找树
简介
满足下面条件就是二叉查找树
- 任意节点左子树不为空,则左子树的值均小于根节点的值.
- 任意节点右子树不为空,则右子树的值均大于于根节点的值.
- 任意节点的左右子树也分别是二叉查找树.
- 没有键值相等的节点.


二叉查找树在最坏的情况下就是会退化成一个有n个节点的线性链
为了防止这些坏情况发生,在二叉查找树的基础上,又做了一些限制,这也就出现了AVL树(平衡二叉查找树),红黑树
二、AVL树(平衡二叉树)
说一下时间复杂度的计算
由2^x=n 得到x=log2n。 所以这个循环的时间复杂度为O(log2n)。
简介
AVL树是带有平衡条件的二叉查找树,一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡,左右子树树高不超过1,和红黑树相比,它是严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差不超过1).不管我们是执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而旋转是非常耗时的,由此我们可以知道AVL树适合用于插入删除次数比较少,但查找多的情况。
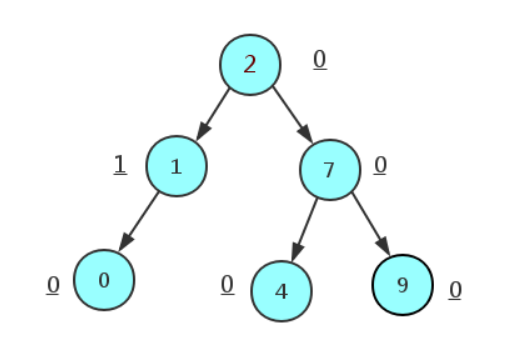
局限性
由于维护这种高度平衡所付出的代价比从中获得的效率收益还大,故而实际的应用不多,更多的地方是用追求局部而不是非常严格整体平衡的红黑树.当然,如果应用场景中对插入删除不频繁,只是对查找要求较高,那么AVL还是较优于红黑树.
查找效率O(log2 n)(2为底)
应用
Windows进程地址空间管理
三、红黑树

简介
一种二叉查找树,但在每个节点增加一个存储位表示节点的颜色,可以是red或black. 通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍.它是一种弱平衡二叉树(由于是若平衡,可以推出,相同的节点情况下,AVL树的高度低于红黑树),相对于要求严格的AVL树来说,它的旋转次数变少,所以对于搜索,插入,删除操作多的情况下,我们就用红黑树.
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log2 n)(2为底)时间内做查找,插入和删除,这里的n 是树中元素的数目。
性质
- 每个节点非红即黑.
- 根节点是黑的。
- 每个叶节点(叶节点即树尾端NUL指针或NULL节点)都是黑的.
- 如果一个节点是红的,那么它的两儿子都是黑的.
- 对于任意节点而言,其到叶子点树NIL指针的每条路径都包含相同数目的黑节点.
应用
- 广泛用于C++的STL中,map和set都是用红黑树实现的.
- 著名的linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块,进程的虚拟内存区域都存储在一颗红黑树上,每个虚拟地址区域都对应红黑树的一个节点,左指针指向相邻的地址虚拟存储区域,右指针指向相邻的高地址虚拟地址空间.
- IO多路复用epoll的实现采用红黑树组织管理sockfd,以支持快速的增删改查.
- ngnix中,用红黑树管理timer,因为红黑树是有序的,可以很快的得到距离当前最小的定时器.
- java中TreeMap的实现.
四、红黑树 VS AVL树
红黑树是通过复杂的节点插入、节点颜色变换后实现的:这些功能经典的AVL树也能实现,为什么要提出红黑树?
首先红黑树是不符合AVL树的平衡条件的,即每个节点的左子树和右子树的高度最多差1的二叉查找树。但是提出了为节点增加颜色,红黑是用非严格的平衡来换取增删节点时候旋转次数的降低,任何不平衡都会在三次旋转之内解决,而AVL是严格平衡树,因此在增加或者删除节点的时候,根据不同情况,旋转的次数比红黑树要多。所以红黑树的插入效率更高!!!
对于插入删除操作很少,又很频繁地查询的,可以用红黑树实现
五、B 树(多叉树)
B-Tree介绍
B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;
B-Tree是一种多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
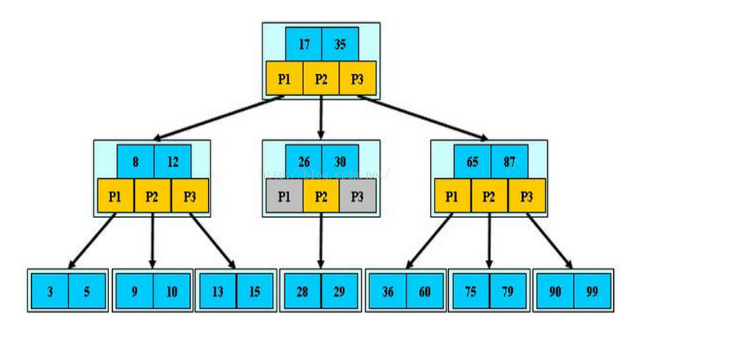
B-树的特性:
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
B+Tree介绍
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
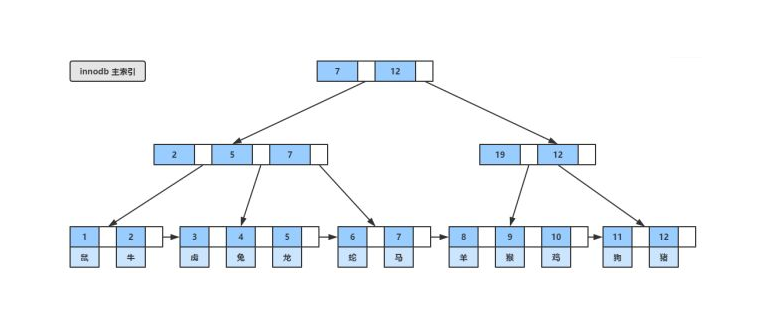
B+的搜索与B-树也基本相同,区别是
B+树只有达到叶子结点才命中(B-树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4.更适合文件索引系统;
B树与B+树区别
这都是由于B+树和B具有这不同的存储结构所造成的区别,以一个m阶树为例。
关键字的数量不同;B+树中分支结点有m个关键字,其叶子结点也有m个,其关键字只是起到了一个索引的作用,但是B树虽然也有m个子结点,但是其只拥有m-1个关键字。
存储的位置不同;B+树中的数据都存储在叶子结点上,也就是其所有叶子结点的数据组合起来就是完整的数据,但是B树的数据存储在每一个结点中,并不仅仅存储在叶子结点上。
分支结点的构造不同;B+树的分支结点仅仅存储着关键字信息和儿子的指针(这里的指针指的是磁盘块的偏移量),也就是说内部结点仅仅包含着索引信息。
查询不同;B树在找到具体的数值以后,则结束,而B+树则需要通过索引找到叶子结点中的数据才结束,也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径
为什么说B+比B树更适合实际应用中操作系统的文件索引和数据库索引?
- B+的磁盘读写代价更低
B+的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
- B+-tree的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
数据库索引采用B+树的主要原因是 B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。正是为了解决这个问题,B+树应运而生。B+树只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作(或者说效率太低)
六、其他二叉树
1、二叉树
是n(n>=0)个结点的有限集合,它或者是空树(n=0),或者是由一个根结点及两颗互不相交的、分别称为左子树和右子树的二叉树所组成。
2、满二叉树
一颗深度为k且有2^k-1个结点的二叉树称为满二叉树。
除叶子结点外的所有结点均有两个子结点。节点数达到最大值。所有叶子结点必须在同一层上。
3、完全二叉树
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号