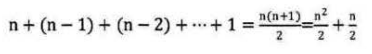算法的时间、空间复杂度详解
一、算法
1、算法是对待定问题求解步骤的一种描述
2、衡量算法的指标:
时间复杂度:执行这个算法需要消耗多少时间,即算法计算执行的基本操作次数
空间复杂度:这个算法需要消耗多少空间,即算法在运行过程中临时占用存储空间大小的度量,强调的是辅助空间的大小(对数据进行操作的工作单元和存储一些计算的辅助单元),而不是指所有数据所占用的空间
3、同一个问题可以用不同的算法解决,而一个算法的优劣将影响到算法乃至程序的效率。算法分析的目的在于为特定的问题选择合适的算法。一个算法的评价主要从时间复杂度和空间复杂度来考虑
算法在时间的高效性和空间的高效性之间通常是矛盾的,通常我们会假设程序运行在足够大的内存中,更多地去探究时间复杂度
二、时间复杂度
常见的时间复杂度有:常数阶O(1),对数阶O(log2n),线性阶O(n),线性对数阶O(nlog2n),平方阶O(n2),立方阶O(n3), k次方阶O(nk),指数阶O(2n)。随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
- 去掉运行时间中的所有加法常数。
- 只保留最高阶项。
- 如果最高阶项存在且不是1,去掉与这个最高阶相乘的常数得到时间复杂度
1、常数阶
int sum = 0, n = 100; /*执行一次*/ sum = (1 + n) * n / 2; /*执行一次*/ printf("%d",sum); /*执行一次*/
2、对数阶
int count = 1; while (count < n){ count = count * 2; /*时间复杂度为O(1)的程序步骤序列*/ }
由于每次count乘以2之后,就距离n更近了一分。 也就是说,有多少个2相乘后大于n,则会退出循环。 由2^x=n 得到x=log2n。 所以这个循环的时间复杂度为O(log2n)。
3、线性阶
int i; for(i = 0; i < n; i++){ /*时间复杂度为O(1)的程序步骤序列*/ }
4、平方阶
int i, j; for(i = 0; i < n; i++){ for(j = 0; j < n; j++){ /*时间复杂度为O(1)的程序步骤序列*/ } }
int i, j; for(i = 0; i < n; i++){ for(j = i; j < n; j++){ /*注意j = i而不是0*/ /*时间复杂度为O(1)的程序步骤序列*/ } }
由于当i=0时,内循环执行了n次,当i = 1时,执行了n-1次,……当i=n-1时,执行了1次。所以总的执行次数为:
5、立方阶
int i, j; for(i = 1; i < n; i++) for(j = 1; j < n; j++) for(j = 1; j < n; j++){ /*时间复杂度为O(1)的程序步骤序列*/ }
三、空间复杂度
1、递归情况
int BinarySearch2(const int* ptr,const int x,const int left,const int right) { int mid=(left+right)/2; while(left<=right) { if(x<ptr[mid]) { return BinarySearch2(ptr,x,left,mid-1); } else if(x>ptr[mid]) { return BinarySearch2(ptr,x,mid+1,right); } return mid; } }
递归情况下的空间复杂度:递归深度为N*每次递归的辅助空间大小,如果每次递归的辅助空间为常数,则空间复杂度为O(N)。
对于递归的二分查找,递归深度是log2^n,每次递归的辅助空间为常数,所以空间复杂度为O(log2N)(2为底数下标)
2、非递归情况
int BinarySearch1(const int* ptr,const int x,const int len) { int left=0; int right=len-1; int mid=(left+right)/2; while(left<=right) { if(x<ptr[mid]) { right=mid-1; } else if(x>ptr[mid]) { left=mid+1; } else { return mid; } } return -1; }
在这个过程中,辅助空间为常数级别,所以空间复杂度为O(1)