LeetCode 72. 编辑距离
72. 编辑距离
Difficulty: 困难
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
提示:
0 <= word1.length, word2.length <= 500word1和word2由小写英文字母组成
Solution
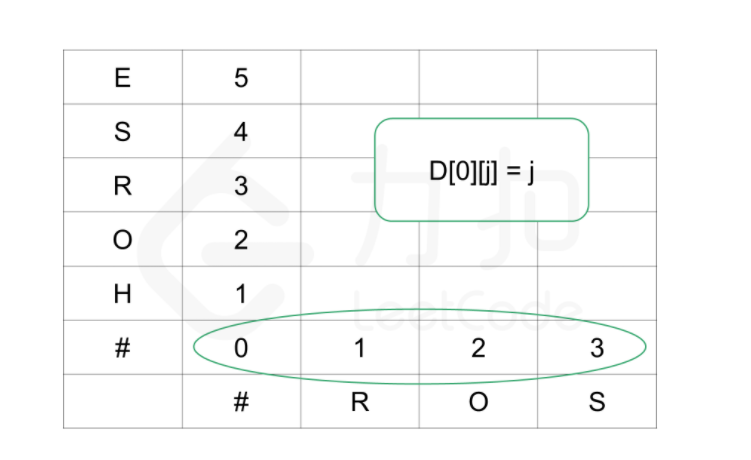
如何从大问题分解为子问题的?
比如abbc和acc两个字符串的编辑距离,因为两个字符串的最后一个字符是相同的,那么它的子问题便变成了求abb和ac两个字符串的编辑距离。
abb和ac两个字符串的最后一个元素不相同,根据题目要求此时可以分成三种情形:
- 删除操作:把
abb的最后一个b删除,求ab和ac的子问题 - 插入操作:对
abb和a,对a插入一个c - 替换操作:知道
ab改成a之后,只用把b替换成c就行了
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
l1, l2 = len(word1), len(word2)
if not l1 or not l2:
return l1+l2
# 初始化一个 (l1+1) * (l2+1) 大小的矩阵
dp = [[0] * (l2+1) for _ in range(l1+1)]
# 初始化矩阵边缘的“编辑距离”
for i in range(l1+1):
dp[i][0] = i
for j in range(l2+1):
dp[0][j] = j
for i in range(1, l1+1):
for j in range(1, l2+1):
# 如果最后一个字符不相同
if word1[i - 1] != word2[j - 1]:
dp[i-1][j-1] += 1
dp[i][j] = min(min(dp[i][j-1], dp[i-1][j]) + 1, dp[i-1][j-1])
return dp[l1][l2]




