LeetCode 46. 全排列

46. 全排列

Difficulty: 中等

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

Solution

全排列系列第一题，涉及到排列或者组合，大概率是考察回溯算法，回顾回溯算法的解题框架：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

然后，问自己两个问题：1. 递归什么时候结束？2. 元素是可以被重复使用的还是不可以被重复使用的？

1. 因为考察的是数组元素的排列，那么当排列的结果等于数组的长度即可
2. 根据题目的要求，数组中的元素不能被重复使用

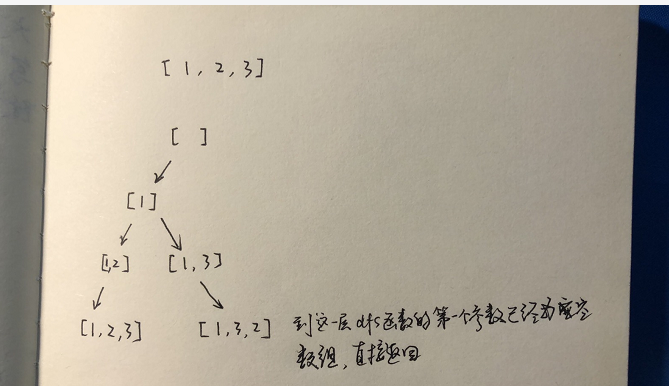
你可以这样区别组合和排列问题，组合问题需要你“一往直前”，而排列问题却需要你时不时“回头看看”，所以在解答排列问题之前我们需要额外建立一个数组used用于标记元素是否有被使用。

解法一：

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        self.res = []
        used = [0] * len(nums)
        self.dfs(nums, [], used, self.res)
        return self.res

    def dfs(self, nums, path, used, res):
        if len(path) == len(nums):
            res.append(path[:])
            return
        for i in range(len(nums)):
            if not used[i]:  # 如果没有被使用才能做选择
                used[i] = True
                path.append(nums[i])
                self.dfs(nums, path, used, res)
                used[i] = False
                path.pop()

解法二：

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        if not nums:
            return []
        res = []
        self.dfs(nums, [], res)
        return res
        
    def dfs(self, nums, path, res):
        if not nums:
            res.append(path)
            return 
        for n in nums:
            self.dfs([i for i in nums if i != n], path + [n], res)