LeetCode 39. 组合总和

39. 组合总和

Difficulty: 中等

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

• 所有数字（包括 target）都是正整数。
• 解集不能包含重复的组合。

示例 1：

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
  [7],
  [2,2,3]
]

示例 2：

输入：candidates = [2,3,5], target = 8,
所求解集为：
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

提示：

• 1 <= candidates.length <= 30
• 1 <= candidates[i] <= 200
• candidate 中的每个元素都是独一无二的。
• 1 <= target <= 500

Solution

很基础的一道考察组合题目，一般排列组合类型的问题考察的就是回溯算法（组合总和IV那道题比较特殊，考察的是动态规划，使用回溯算法会超时）。有很多大佬总结过回溯算法经典解题框架（套路），简单来说就是：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

用这个框架来解决问题的时候，需要注意两个问题：1. 递归什么时候结束？2. 元素是可以被重复使用的还是不可以被重复使用的？

回到这个题目，题目给定了无重复元素的数组，并且数组内的元素可以被重复使用，只要保证从数组内选择的元素求的和等于target就行了。好，现在我们考虑上文提到需要考虑的两个问题：1. 数组内元素每次被使用之后，target减去该元素，直到target被减到0，说明找到了满足和为target的组合。2. 题目交代数组内的元素可以被重复使用，那么选择的列表就是candidates。回答了这两个问题，剩下的代码就好办了。

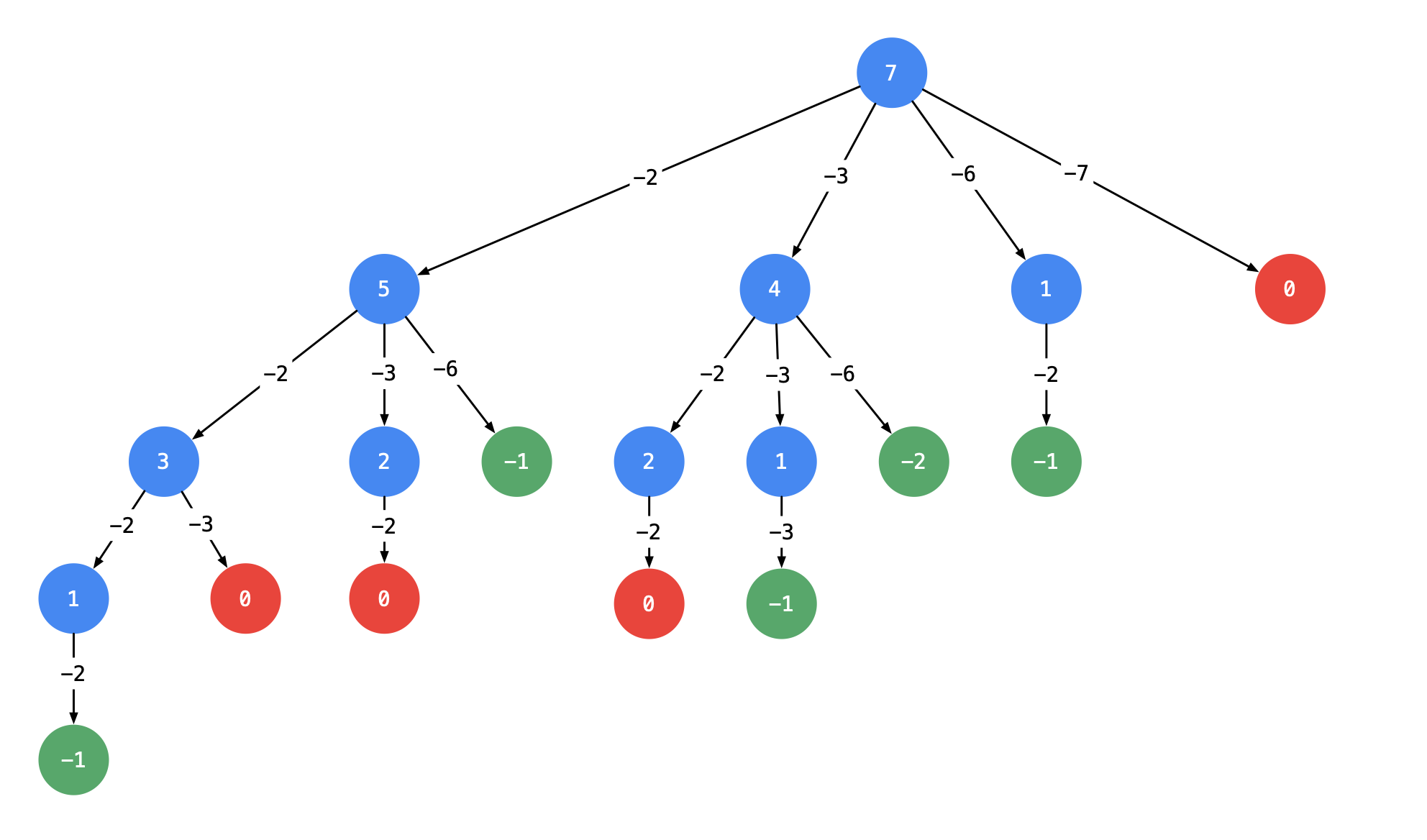
解法一：

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:       
        path = []
        res = []
        self.backtrack(candidates, path, target, res)
        return res
        
    def backtrack(self, nums, path, target, res):
        if target < 0:
            return
        if target == 0:
            res.append(path[:])
            return
        for i in range(len(nums)):
            path.append(nums[i])
            self.backtrack(nums, path, target-nums[i], res)
            path.pop()

解法二：

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        res = []
        self.dfs(candidates, target, [], res)
        return res
        
    def dfs(self, nums, target, path, res):
        if target < 0:
            return
        if target == 0:
            res.append(path)
            return
        for i in range(len(nums)):
            self.dfs(nums[i:], target-nums[i], path+[nums[i]], res)