大数据之统计学基础
1. 统计学
统计学可以分为：描述统计学与推断统计学
描述统计学：使用特定的数字或图表来体现数据的集中程度和离散程度。例：每次考试算的平均分，最高分，各个分段的人数分布等，也是属于描述统计学的范围。
推断统计学：根据样本数据推断总体数据特征。例：产品质量检查，一般采用抽检，根据所抽样本的质量合格率作为总体的质量合格率的一个估计。
2.均值、中位数、总数、极差、方差、标准差
对于一组数组，如果只容许使用一个数字去代表这组数据，那么这个数字应该如何选择？？——选择数据的中心，即反映数据集中趋势的统计量。
均值——算术平均数，描述平均水平。
中位数——将数据按大小排列后位于正中间的数描述，描述中等水平。
众数——数据中出现最多的数，描述一般水平。
极差——最大值-最小值，简单地描述数据的范围大小
方差——在统计学上，更常用的是使用方差来描述数据的离散程度——数据离中心越远越离散。其中，X¡表示数据集中第i个数据的值，µ表示数据集的均值。
标准差——如果原数据的单位是m的话，那么方差的单位就是mˆ2，方差与原数据的单位是不一样的，两者没有可比性。为了保持单位的一致性，我们引入一个新的统计量——标准差。
2.1 均值
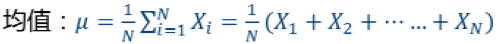
2.2 中位数
顾名思义，中位数就是将数据按大小顺序（从大到小或是从小到大都可以）排列后处于中间位置的数。若处于中间位置的数据有两个（也就是数据的总个数为偶数时），中位数为中间两个数的算术平均数。
2.3 众数
众数——数据中出现次数最多的数（所占比例最大的数）。一组数据中，可能会存在多个众数，也可能不存在众数。众数不仅适用于数值型数据，对于非数值型数据也同样适用。
2.4 均值、中位数、众数的优劣势
| 优点 | 缺点 | |
| 均值 | 充分利用所有数据，适用性强 | 容易受到极端值影响 |
| 中位数 | 不受极端值影响 | 缺乏敏感性 |
| 众数 | 当数据具有明显的集中趋势时，代表性好；不受极端值影响 | 缺乏唯一性：可能有一个，可能有两个，可能一个都没有 |
2.5 方差
方差公式：
，方差公式经过变形后可以简化为
。
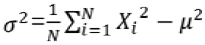方差分总体方差与样本方差。总体方差：
，样本方差：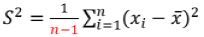
2.6 标准差
标准差：
，有效地避免了因单位平方而引起的度量问题。与方差一样，标准差的值越大，表示数据越分散。
3. 统计学直观图表
原数据太杂乱无章，难以看出规律性；只依赖数字来描述集中趋势与离散程度，让人难以对数据产生直观的印象，这时就需要用到图表。
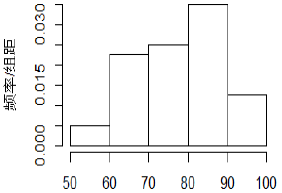
3.1 直方图
频数分布表
频数直方图
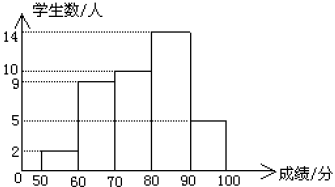
频率直方图
3.2 箱线图
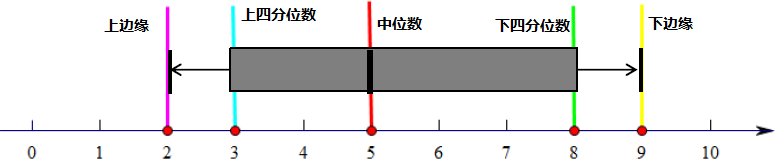
上边缘：除异常点以外的数据中的最大值
上四分位数：将所有数据按照从小到大的顺序排序排在第75%位置的数字
下四分位数：将所有数据按照从小到大的顺序排序排在第25%位置的数字
下边缘：除异常点以外的数据中的最小值
3.3 茎叶图
将数据分为茎和叶两部分，这里的茎是指十位上的数字，叶是指个位上的数字。将茎部分(十位)从小到大，从上到下写出来。相对于各自的茎，将同一茎(十位)的叶子(个位)从小到大，从左往右写出来。
3.4 线图
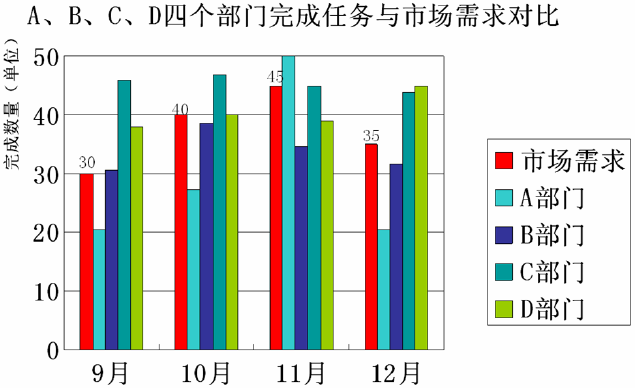
3.5 柱形图
柱形图：显示一段时间内的数据变化或显示各项之间的比较情况。
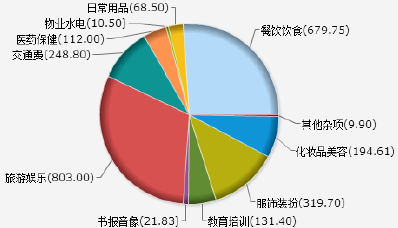
3.6 饼状图
饼状图，根据各项所占百分比决定在饼图中的扇形面积。简单易懂，通俗明了，可以更加形象地看出各个项目所占的比例大小。
4. 概率论
4.1 条件概率
已知某个事件A发生的条件下，另一个事件B发生的概率称为条件概率，记为P(B|A)。看一下P(B|A)与P(A)、P(B)的关系：P(B|A) = P(AB) / P(A)。
条件概率也是概率的一种，所以也符合概率定义的三个条件：
- 非负性：P(B|A) ≥ 0；
- 规范性：对于必然事件S，有P(S|A) = 1；
- 可列可加性：对于两两互不相容的事件B1，B2，B3.....，即Bi · Bj = Ø，i ≠ j，i，j = 1，2，......，有P(B1 υ B2 υ ...... | A) = P(B1|A) + P(B2|A) + ......
乘法定理：由条件概率的定义，很容易得到P(AB) = P(B|A)P(A)，其中P(A) > 0；这条公式很容易推广到P(ABC) = P(C|AB)P(B|A)P(A) = P(A|BC)P(B|C)P(C).
4.2 全概率公式
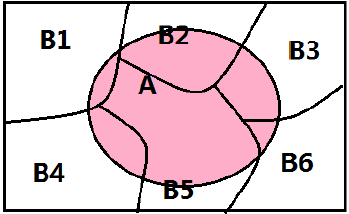
设试验E的样本空间为S，A为E的一个事件，B1、B2......Bn是S的一个划分，且P(Bi) > 0 (i=1,2......n)，则
在某些时候，事件A的概率不好求，但是通过全概率公式却可以很容易求得。
4.3 贝叶斯公式
设试验E的样本空间为S。A为E的一个事件，B1、B2......Bn是S的一个划分，且P(A) > 0, P(Bi) > 0 (i=1,2,.....,n)，则
当对样本空间的划分由一对对立事件B与¯B组成时，全概率公式和贝叶斯公式可以简化为
贝叶斯公式的应用——诉讼、疾病诊断、垃圾邮件判别
下面来看一则案例：
4.4 公式比较
乘法公式、全概率公式与贝叶斯公式
- 乘法公式是求“几个事件同时发生”的概率；
- 全概率公式是求“最后结果”的概率；
- 贝叶斯公式是已知“最后结果”，求“某个事件”的概率。
先验概率与后验概率
- P(Bj|A)是在事件A发生的条件下，某个事件Bj发生的概率，称为“后验概率”；
- Bayes公式又称为“后验概率公式” 或 “逆概公式”；
- 称P(Bj)为“先验概率”。
4.5 独立性与事件
设A、B是两个事件，如果满足：P(AB) = P(A)P(B)，则称事件A、B相互独立。简称A、B独立。
由事件独立的定义可以推出：
- A、B独立，且P(A) > 0 ↔ P(B|A) = P(B)。
P(B|A) = P(AB)/P(A) = P(A)P(B) /P(A) = P(B)
- 若A、B独立，则A与¯B、¯A与¯B也相互独立。
P(A) = P(A|B)P(B) + P(A|¯B)P(¯B) = P(A)P(B) + P(A¯B)
故P(A¯B) = P(A) - P(A)P(B) = P(A)(1-P(B))=P(A)P(¯B)
设A、B、C是三个事件，若满足
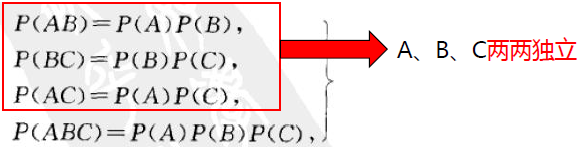
则称A、B、C相互独立。
4.6 相互独立事件与互斥事件、对立事件
相互独立事件：两个事件没有一点关系。
互斥事件：要么只有其中一个事件发生，要么两个事件都不发生。
对立事件：两个之中，只有一个发生。跟互斥事件相比，对立事件必然会有一个事件发生。
互斥事件与对立事件都不是相互独立事件！
