数据结构-二叉树、B树、B+树、B*树（整理版）
1. 二叉树
二叉树的特点：
① 所有非叶子节点至多拥有两个儿子（Left和Right）；
② 所有节点存储一个关键字；
③ 非叶子节点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；
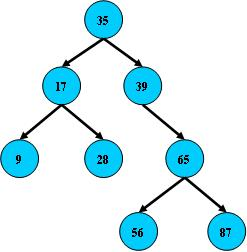
二叉树的搜索，从根节点开始，如果查询的关键字与结点的关键字相等，那么就命中；否则，如果查询关键字比节点关键字小，就进入左儿子；如果比节点关键字大，就进入右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字；
如果二叉树的所有非叶子节点的左右子树的节点数目均保持差不多（平衡），那么二叉树的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变二叉树结构（插入与删除节点）不需要移动大段的内存数据，甚至通常是常数开销；
2. B-树
B-树是一种多路搜索树（并不是二叉的），特点：
① 定义任意非叶子节点最多有M个儿子；且M>2；
② 根节点的儿子数为[2, M]；
③ 除了根节点以外的非叶子节点的儿子数为[M/2，M]；
④ 每个节点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）
⑤ 非叶子节点的关键字个数 = 指向儿子的指针个数-1；
⑥ 非叶子节点的关键字：K[1], K[2]，...，K[M-1]；且K[i] < K[i+1]；
⑦ 非叶子节点的指针：P[1],P[2],...P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；
⑧ 所有叶子节点位于同一层，如：（M=3）
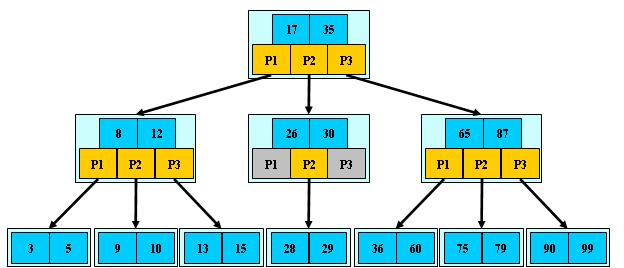
B-树的搜索，从根节点开始，对节点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子节点；重复，直到所对应的儿子指针为空，或已经是叶子节点；
3. B+树
B+树的特点：
① 其定义基本与B-树同，除了：
② 非叶子节点的子树指针与关键字相同；
③ 非叶子节点的子树指针P[i]，指向关键字值属于(K[i], K[i-1])的子树（B-树是开区间）；
④ 为所有叶子节点增加一个链指针；
⑤ 所有关键字都在叶子结点出现，如：（M=3）
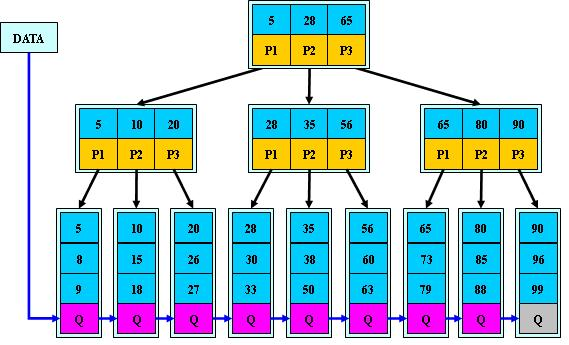
B+树的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；
4. B*树
B*树是B+树的变体，在B+树的非根和非叶子节点再增加指向兄弟的指针；
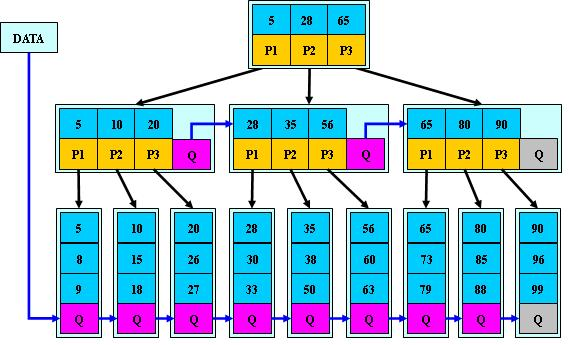
【总结】
https://www.cnblogs.com/yichengming/p/11176490.html B树、B+树、B*树三者的对比详解
https://www.i3geek.com/archives/711 树——多路数，B树、B-树、B+树、B*树
https://blog.csdn.net/nashouat/article/details/8494946 二叉树、B-树、B+树、B*树
