WPF3D立方体图形展开动画思路
WPF3D立方体图形展开动画
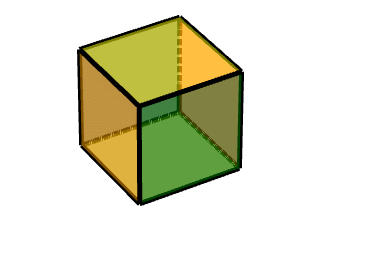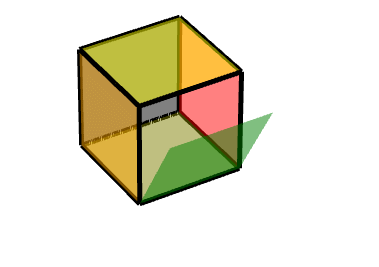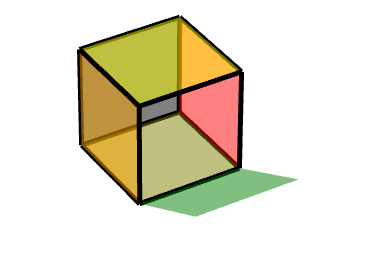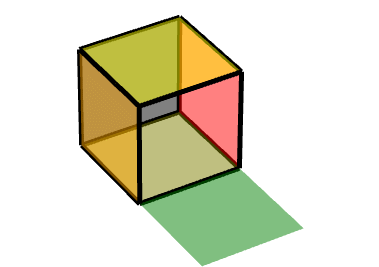
效果图:
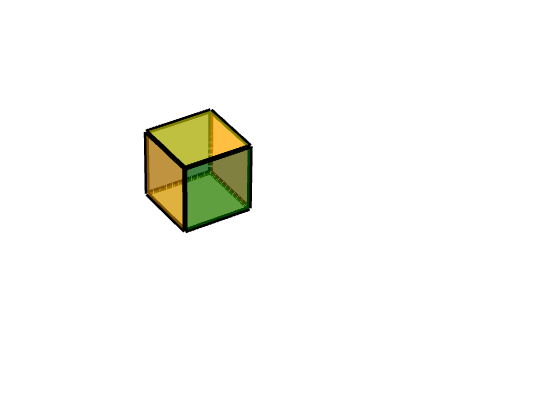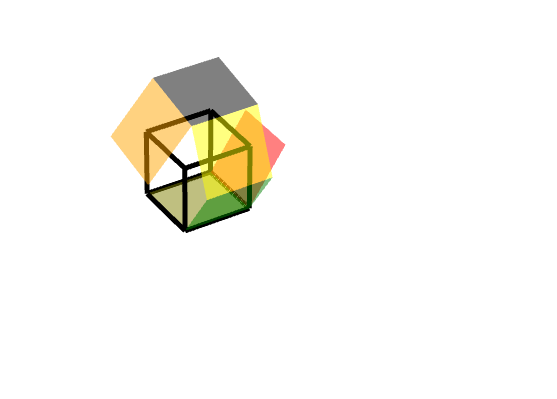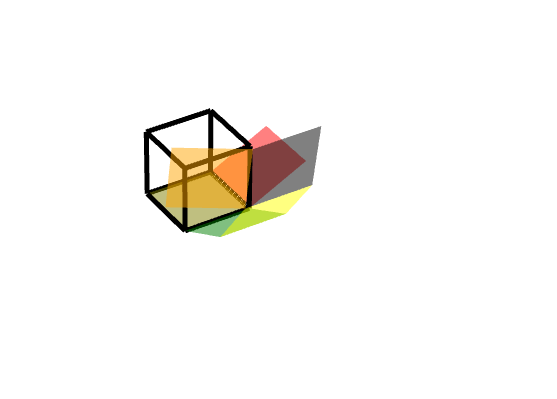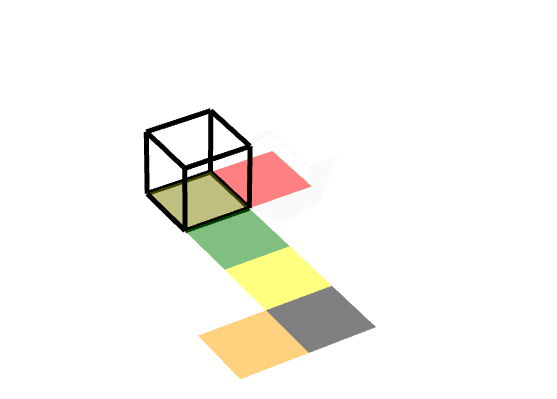
规定:
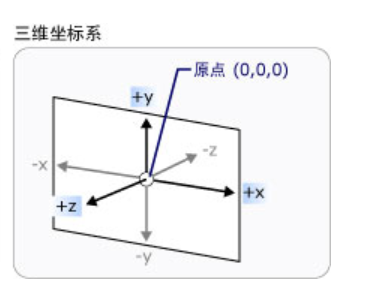
立方体中心为(000),棱长为2,则(111)(-1-1-1)等1,-1三维组合的八个点为其顶点
坐标系:
补充:
WPF 3D 分为中心对称旋转(RotateTransform3D),平移旋转(TranslateTransform3D)和比例缩减(ScaleTransform3D),立体图形展开目前只用到对称和平移变换
1 按轴旋转的面
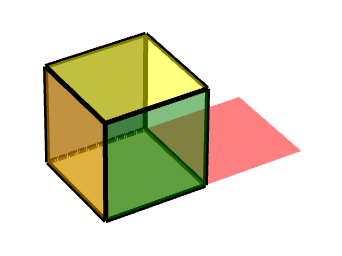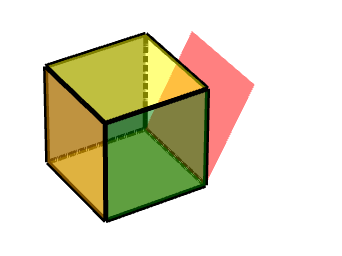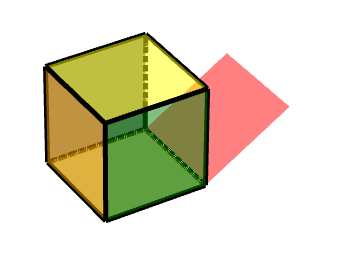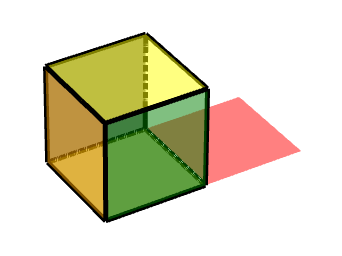
如图所示,则其是按照由(-1-1-1)到(1-1-1)的轴运动
换算成中心对称,也就是这条边的中点,则对称点为(0,-1,-1)
此动画可描述为,对点(0,-1,-1)做中心对称变换,沿X轴旋转90度。
Code:
//设置对称中心
face0RotateTransform3D.CenterX = 0;
face0RotateTransform3D.CenterY = -1;
face0RotateTransform3D.CenterZ = -1;
//设置旋转角度
(face0RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(1, 0, 0);
DoubleAnimation face0AxisAngleRotation3DAnimation = new DoubleAnimation();
face0AxisAngleRotation3DAnimation.From = 0;
face0AxisAngleRotation3DAnimation.To = -90;
face0AxisAngleRotation3DAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));
同理可得另一个面:对点(1,-1,-1)做中心对称变换,沿Z轴旋转90度。
Code:
face3RotateTransform3D.CenterX = 1;
face3RotateTransform3D.CenterY = -1;
face3RotateTransform3D.CenterZ = -1;
(face3RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 0, 1);
DoubleAnimation DoubleAnimation = new DoubleAnimation();
DoubleAnimation.From = 0;
DoubleAnimation.To = -90;
2 连接按轴旋转的面的面
即二级旋转面
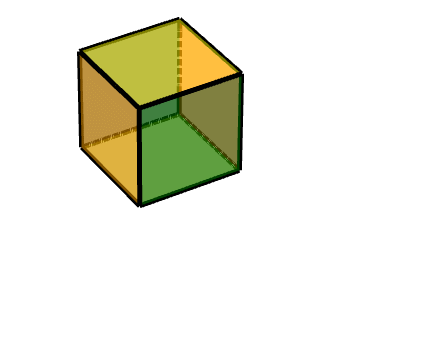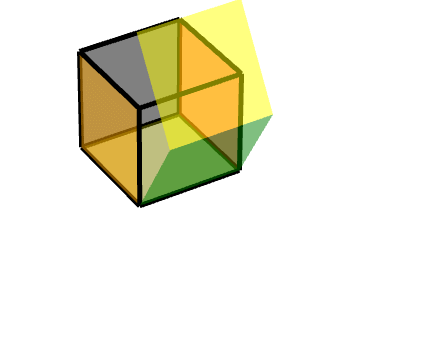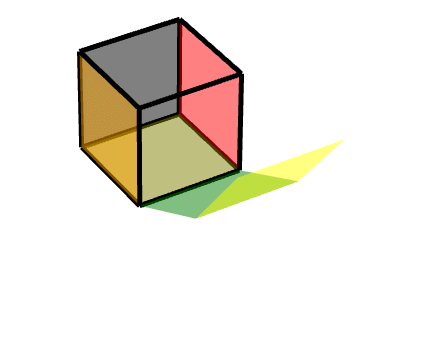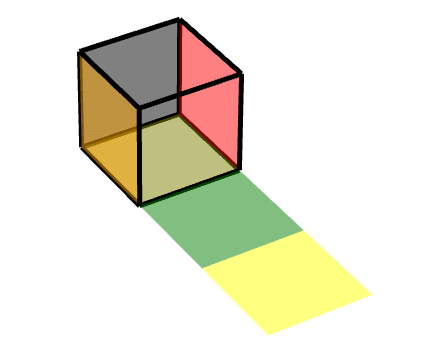
此时,我们可以把它理解为两个旋转的结合,一个轴对称旋转+一个平移旋转
1 轴对称旋转:
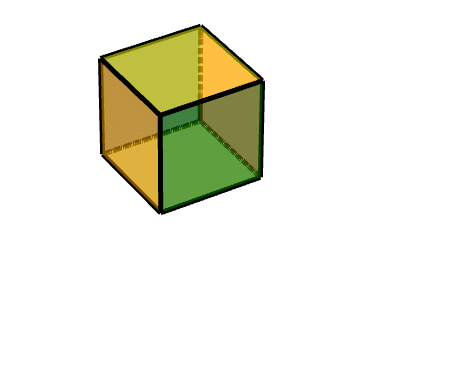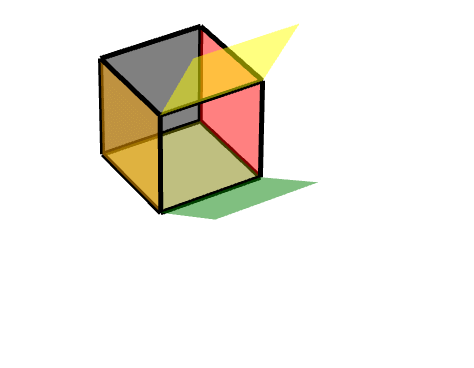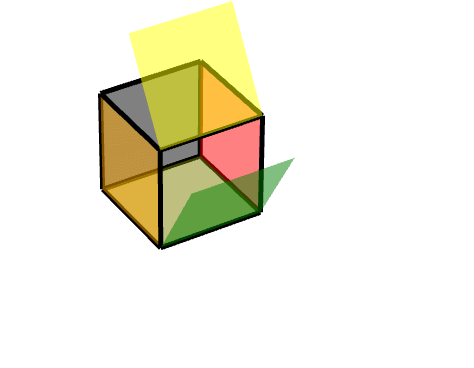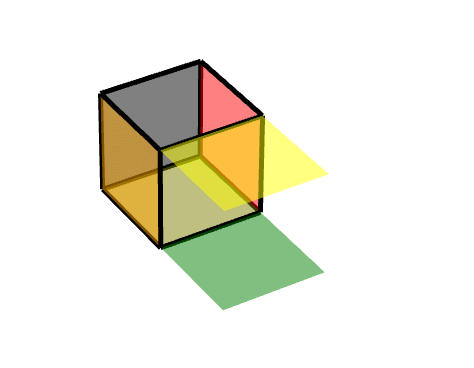
描述为,对点(11-1)进行旋转,沿Z轴旋转180度。
Code:
face4RotateTransform3D.CenterX = 1;
face4RotateTransform3D.CenterY = 1;
face4RotateTransform3D.CenterZ = -1;
(face4RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 0, 1);
DoubleAnimation DoubleAnimation = new DoubleAnimation();
DoubleAnimation.From = 0;
DoubleAnimation.To = -180;
2 平移旋转:
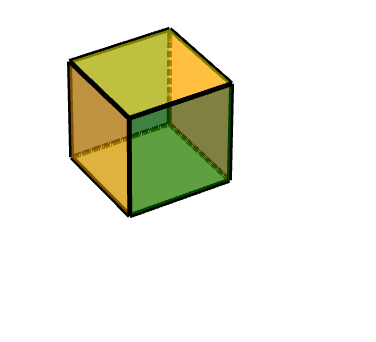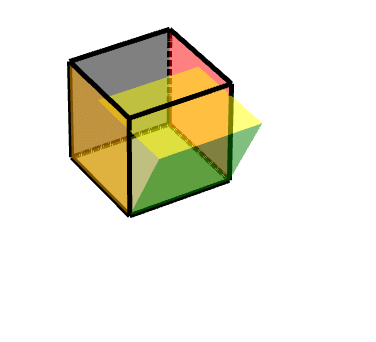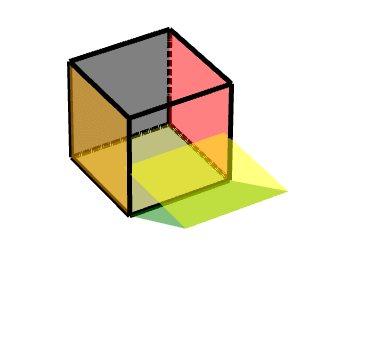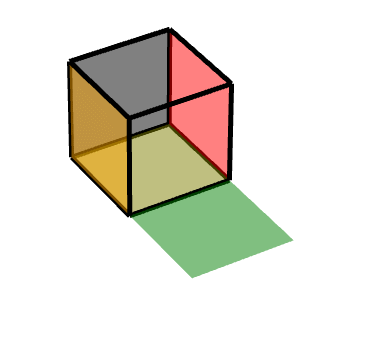
从侧面看的平移轨迹:
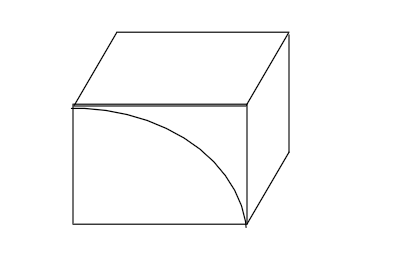
此平移按X和Y轴方向分解示意图:
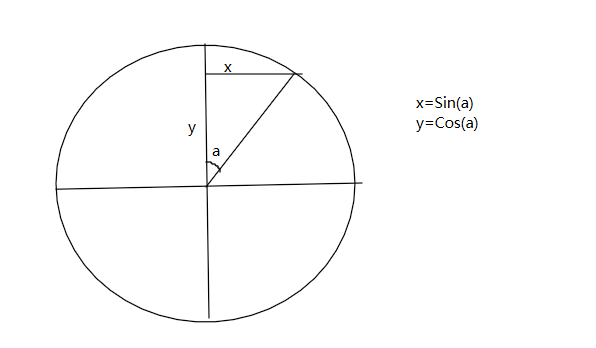
其中X方向可以描述为:
在t时间内,L为边长
x方向值为:x=L*Sin(a)
y方向值为:y=L*Cos(a)
其中角度a可描述为:(PI/2)*currentTime/totalAnimationDuration
如果我们将动画描述成帧动画,综上:
X方向平移动画帧
LinearDoubleKeyFrame GetFace4OffsetXKeyFrame(double time)
{
return new LinearDoubleKeyFrame(borderLength * Math.Sin(time * (Math.PI / 2) / keyFrameAnimationTotalTimeM), KeyTime.FromTimeSpan(TimeSpan.FromSeconds(time)));
}
Y方向平移动画帧
LinearDoubleKeyFrame GetFace4OffsetYKeyFrame(double time)
{
return new LinearDoubleKeyFrame(-(borderLength - borderLength * Math.Cos(time * (Math.PI / 2) / keyFrameAnimationTotalTimeM)), KeyTime.FromTimeSpan(TimeSpan.FromSeconds(time)));
}
3 三级旋转面
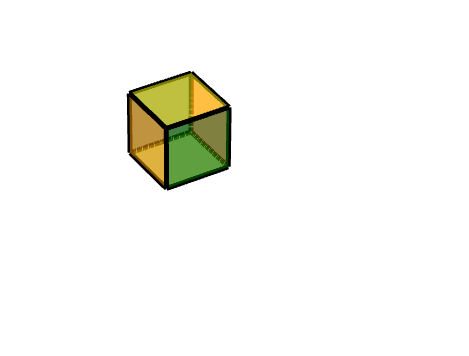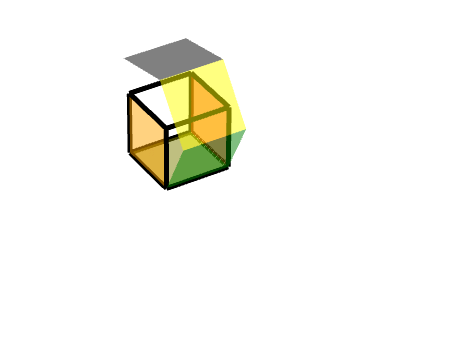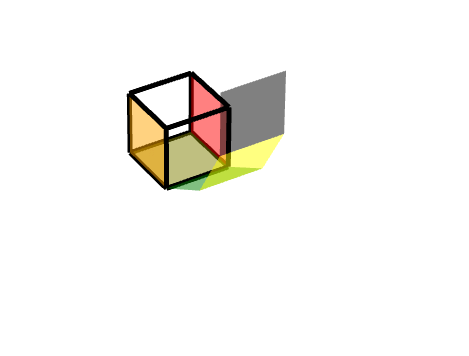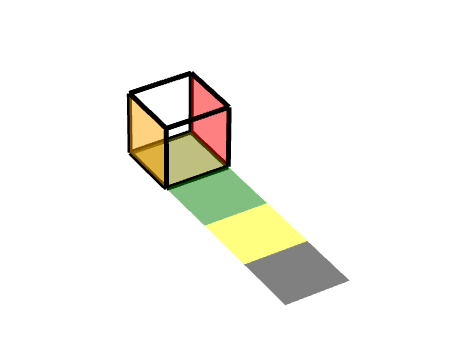
同理,我们可以把它理解为两个旋转的结合,一个轴对称旋转+一个平移旋转
轴对称旋转:

描述为,对点(-110)进行旋转,沿Z轴旋转270度。
Code:
face1RotateTransform3D.CenterX = -1;
face1RotateTransform3D.CenterY = 1;
face1RotateTransform3D.CenterZ = 0;
(face1RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 0, 1);
DoubleAnimation DoubleAnimation = new DoubleAnimation();
DoubleAnimation.From = 0;
DoubleAnimation.To = -270;
DoubleAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));
平移旋转:
平移旋转的量需要通过分解轴旋转来得出。
通过观察我们可以将其分为两个轴旋转,第一个旋转是该面沿着A轴的轴对称旋转(自身旋转),第二个是二级面的沿着B轴的轴对称旋转(相对面旋转)
A棱边沿着A·轨迹旋转,B棱边沿着B·轨迹旋转
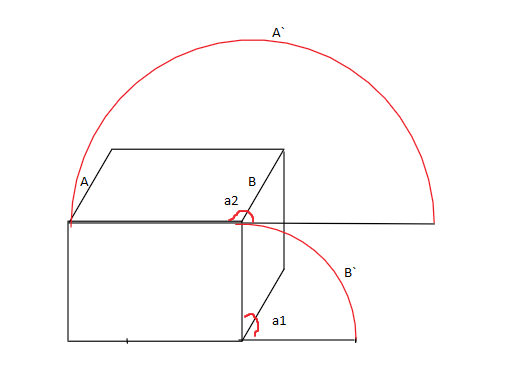
则沿着B轴的旋转,与二级面分解一样:
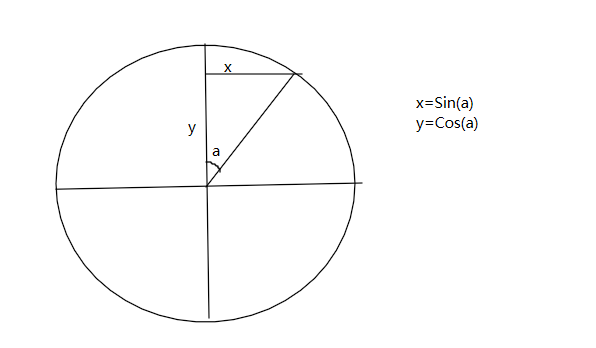
A轴旋转分解:
对于y,y=Sin(a2)
对于x,分为两种情况:
当a2处于0-PI/2时,x=Cos(a2),
当a2处于PI/2-PI时,y=L-Cos(a2)

把上述两个分解加一起就得到了X=xa+xb,y=ya+yb,
Code:
X
LinearDoubleKeyFrame GetFace1OffsetXKeyFrame(double time)
{
//自身边的定位坐标
double angle = time / keyFrameAnimationTotalTimeM;
double xa, xb;
double xTotal;
if (angle <= 1 / 2)
{
//0-1/2PI
xa = borderLength * Math.Cos(Math.PI * time / keyFrameAnimationTotalTimeM);
}
else
{
//1/2PI-PI
xa = borderLength - borderLength * Math.Cos(Math.PI * time / keyFrameAnimationTotalTimeM);
}
//前轴定位坐标
xb = borderLength * Math.Sin((Math.PI / 2) * time / keyFrameAnimationTotalTimeM);
xTotal = xa + xb;
return new LinearDoubleKeyFrame(xTotal, KeyTime.FromTimeSpan(TimeSpan.FromSeconds(time)));
}
Y
Timeline Face1ExpandedAnimation_MoveOffsetY_UsingKeyFrames()
{
DoubleAnimationUsingKeyFrames DoubleAnimation = new DoubleAnimationUsingKeyFrames();
DoubleAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));
DoubleAnimation.Completed += ((sender, e) =>
{
faceStoryboard.Remove(tileButton);
});
Storyboard.SetTargetName(DoubleAnimation, "face1TranslateTransform3D");
Storyboard.SetTargetProperty(DoubleAnimation,
new PropertyPath(TranslateTransform3D.OffsetYProperty));
for (double i = 0; i <= keyFrameAnimationTotalTimeM + keyFrameAnimationIntervalM; i += keyFrameAnimationIntervalM)
{
DoubleAnimation.KeyFrames.Add(GetFace1OffsetYKeyFrame(i));
}
return DoubleAnimation;
}C
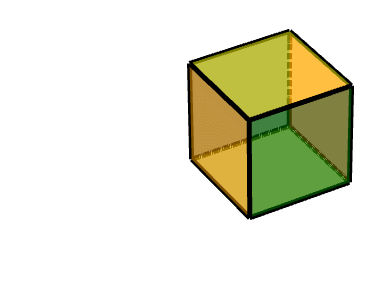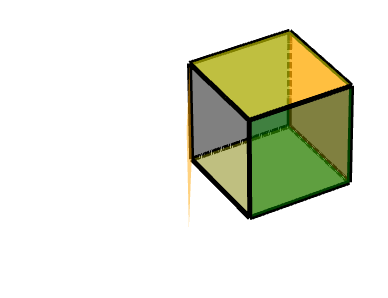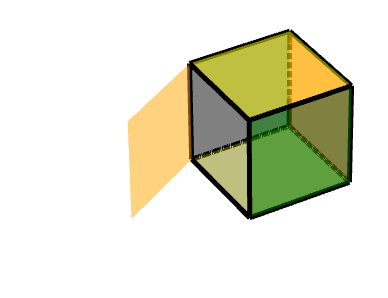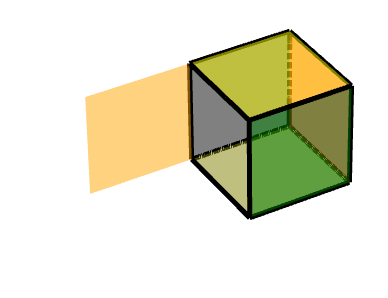
4 双重轴对称旋转+平移旋转面
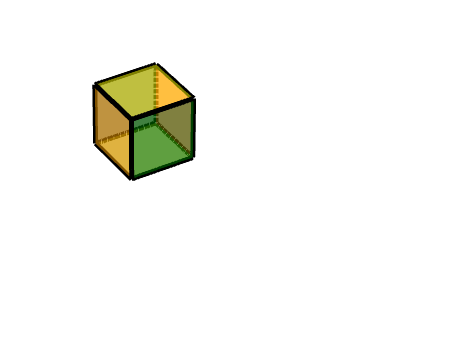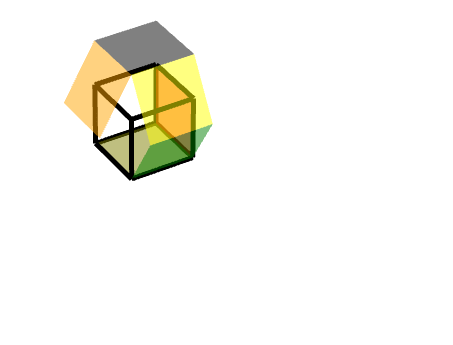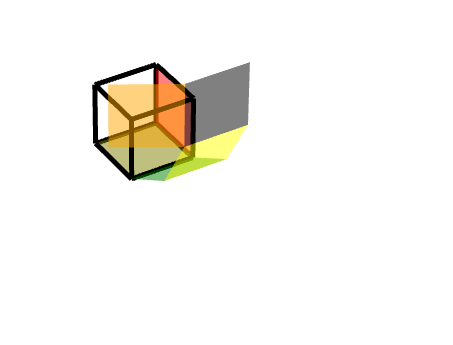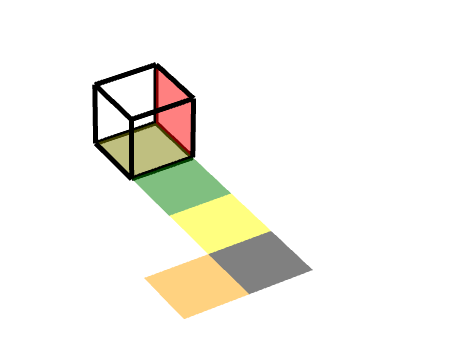
如图所示,左边这个橙色的面,在黑色的三级旋转面之上又增加一个沿着Z轴的旋转。
此时可以简单地分解为三级旋转面的旋转+沿着Z轴的旋转。
三级旋转面的旋转:
见上文
Z轴旋转
可描述为:对点(-1-11)进行旋转,沿Z轴旋转90度。
face5RotateTransform3D.CenterX = -1;
face5RotateTransform3D.CenterY = -1;
face5RotateTransform3D.CenterZ = 1;
(face5RotateTransform3D.Rotation as AxisAngleRotation3D).Axis = new Vector3D(0, 1, 0);
DoubleAnimation DoubleAnimation = new DoubleAnimation();
DoubleAnimation.From = 0;
DoubleAnimation.To = -90;
DoubleAnimation.Duration = new Duration(TimeSpan.FromSeconds(keyFrameAnimationTotalTimeM));



 浙公网安备 33010602011771号
浙公网安备 33010602011771号