数据结构-八大排序

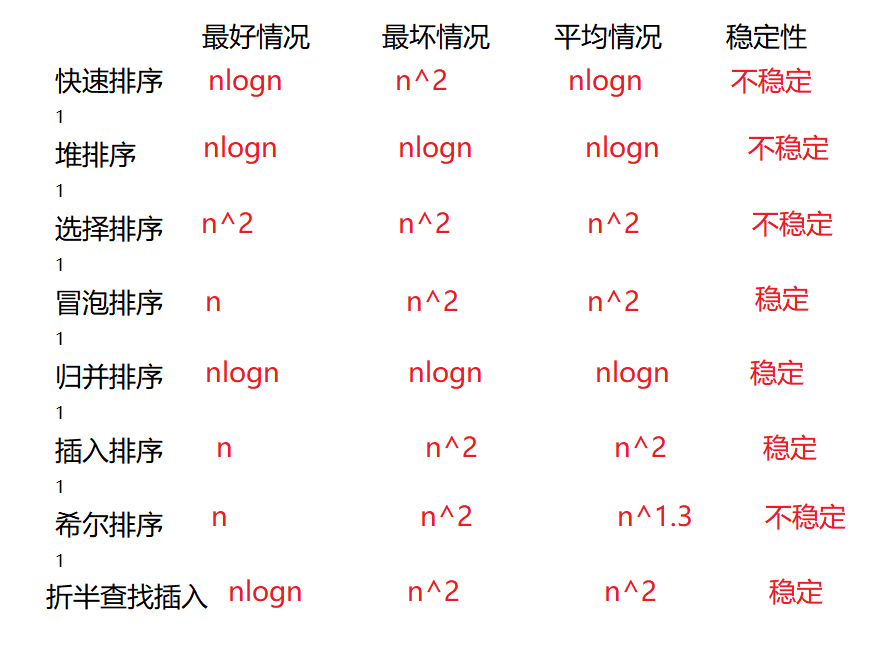
稳定的排序算法：

直接插入排序、折半插入排序、归并排序、冒泡

不稳定的算法：

堆排序、简单选择排序、希尔排序、快速排序

插入排序

时间复杂度为平均情况下\(O(n^2)\)，最坏情况下\(O(n^2)\)，最好情况\(O(n)\)

//插入排序 (下标从1开始存放元素) （王道数据结构）
void InsertSort(int a[], int n) {
	int i, j;
	for ( i = 2; i <= n; i++) {
		if (a[i] < a[i - 1]) {

			a[0] = a[i]; //数组首位位缓存区，也就是哨兵

			for ( j = i - 1; a[0] < a[j]; j--) //从后往前找其插入位置
				a[j + 1] = a[j]; //若当前比较到这个数比哨兵来的大，这个数往后挪

			a[j + 1] = a[0]; //复制到插入的位置
		}
	}

	/*也可以写成这样子*/

	for (int i = 1; i < n; i++) {
		int end = i;
		int temp = a[end + 1];
		while (end >= 1) {
			if (temp < a[end]) {
				a[end + 1] = a[end];
				end--;
			} else break;
		}
		a[end + 1] = temp;

	}
}

希尔排序

时间复杂度为最差\(O(n^2)\)，平均约为\(O(n^{1.3})\)

本质上就是在插入排序的基础上加入对应的增量

void ShellSort(int a[], int n) {
	//a[0]位暂存位置
	int dk, i, j; //dk为增量

	for (dk = n / 2; dk >= 1; dk /= 2) { //增量变化，根据题意去修改

		for ( i = dk + 1; i <= n; i++)
			if (a[i] < a[i - dk]) {
				a[0] = a[i]; //暂存元素

				for (j = i - dk; j >= 1 && a[0] < a[j]; j -= dk)
					a[j + dk] = a[j]; //若当前元素大于a[0]挪对应增量的位置

			}
		a[j + dk] = a[0];//插入对应位置

	}





}



/*也可以写成这样子*/

void ShellInsert(int a[], int dk) { //这个是传入增量
	//
	int n = lena; //假设已知a的长度
	for (int i = 1; i <= n - dk; i++) {
		int id = i;
		int tmp = a[id + dk];
		while (id >= 1) {
			if (tmp < a[id]) {
				a[id + dk] = a[id];
				id -= dk;
			} else break;
		}
		a[id + dk] = tmp;
	}


}

冒泡排序

时间复杂度最好为\(O(n)\)，最坏和平均情况下都为\(O(n^2)\)

void BubbleSort(int a[], int n) {

	for (int i = 0; i < n - 1; i++) {
		for (int j = n - 1; j > i; j--) {
			if (a[j - 1] > a[j]) swap(a[j - 1], a[j]);
			//要得到从小到大排序，从后往前扫，如果前面的元素大于后面的元素就交换
		}

	}

}

选择排序

时间复杂度最好、最坏、平均都是\(O(n^2)\)

void SelectSort(int a[],int n)
{
	for(int i=0;i<n-1;i++)//一共进行n-1趟
	{
		int mi=i;//记录最小元素位置
		for(int j=i+1; j<n; j++) 
			if(a[j]<a[mi]) mi=j;//更换最小值位置
		if(mi!=i) swap(a[i],a[mi]);//交换元素
	}
}

快速排序

时间复杂度为最好为\(o(nlog_2n)\)，最坏\(O(n^2)\)

int Part(int a[],int l,int r)
{
	int piv=a[l]; //将当前表中的第一个元素设为枢轴，对表进行划分
	while(l<r){
		while(l<r && a[r]>=piv) r--; //找到比枢轴小的元素
		a[l]=a[r];//把小的元素移动到左端
		while(l<r&& a[r]<=piv) l++;
		a[r]=a[l];//把大的元素移动到右端
	}
	a[l]=piv;
	return l;
}

void QuickSort(int a[],int l,int r)
{
	if(l<r){
		int pivpos=Part(a,l,r);//划分
		QuickSort(a,l,pivpos);//对子表进行递归的排序
		QuickSort(a,pivpos+1,r);
	}
	
}

归并排序

时间复杂度为最好为\(o(nlog_2n)\)

//int tmp[]
void MergeSort(int a[],int l,int r)
{
	if(l>=r) return ;
	int mid= (l+r) >>1;
	MergeSort(a,l,mid);//左侧子序列递归排序
	MergeSort(a,mid+1,r);//右侧子序列递归排序
	
	int k=0,i=l,j=mid+1;
	while(i<=mid &&j<=r)
	{
		if(a[i]<=a[j] )  tmp[k++]=a[i++];
		else tmp[k++] =a[j++];
	}
	//未检测完的继续复制进去
	while(i<=mid) tmp[k++]=a[i++]; //所有的索引记得都要++ 不然就段错误了
	while(j<=r) tmp[k++]=a[j++];
	
	for(i=l,j=0;i<=r;i++,j++) a[i]=tmp[j];
}