堆排序的原理 以及堆的建立

堆的定义

堆的定义如下，n个关键字序列$L[1....n]$称为堆，当且仅当序列满足：

1. $L(i)>=L(2i)$且$L(i)>=L(2i+1)$ $$ ($1<=i<=n/2$)
   或者
2. $L(i)<=L(2i)$且$L(i)<=L(2i+1)$ $$ ($1<=i<=n/2$)

堆的性质与特点
可以将堆视为一颗完全二叉树，满足条件1的称为大根堆，大根堆的最大元素存放在根节点，且其任意一个非根结点的值小于等于其双亲结点值，满足条件2的称为小根堆，小根堆的定义刚好相反，根节点是最小元素。

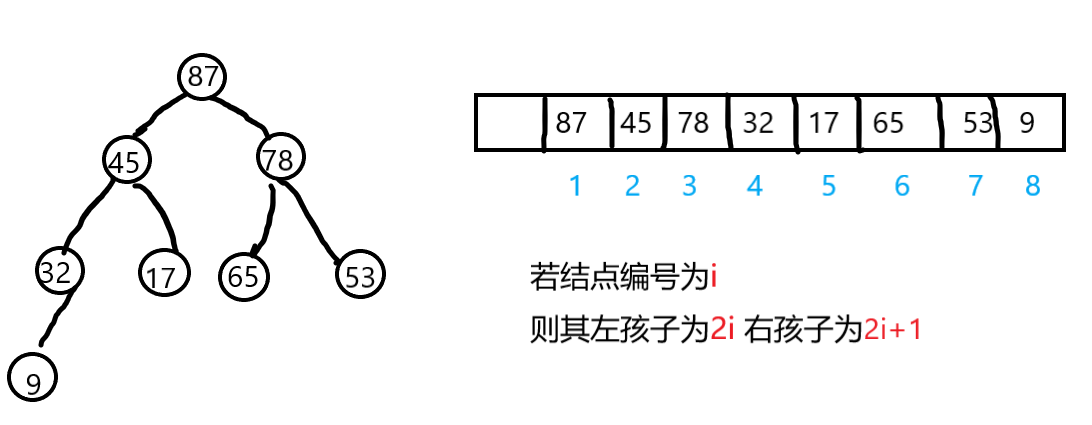
如图所示为一个大根堆

建立堆的原理
本质上就是每个根节点跟其孩子结点比较，如果符号条件就交换，进行完一次以后，又与孩子的孩子结点进行比较，直至不再可以进行交换。

堆排序的原理
将堆顶元素与堆底元素进行交换，此时堆顶元素作为一个已经排好序的数放在堆数组的尾部，从这些未被排好序的元素重新建堆，在重复上述的过程，直到所有元素处理完。

大根堆的建立

1. 检查当前结点是否满足 根>=左、右，若不满足，则将根与值更大的孩子结点进行交换。

2. 若元素互换破坏了下一层的堆则采用相同的方式继续往下调整（小元素不断下坠）。

#include <bits/stdc++.h>
using namespace std;
int n, m;
int h[100005];
 
//--------调整堆的元素-------
void Heapadjust(int k, int len) { 
	//k为该根元素的下标
	//若要建立小根堆 改相应符号即可
 
	int tmp = h[k]; //tmp用来存这颗子树的根节点的值
	for (int idx = k * 2; idx <= len; idx *= 2) { //乘以二原理是孩子的结点的下标
		if (idx < len && h[idx] < h[idx + 1]) idx++; //大根堆拿更大的孩子去交换
		if (h[idx] < tmp) break; //较大的孩子结点也小于根结点 说明不交换
		h[k] = h[idx]; //交换
		k = idx; //元素下坠，意思就是这一层的孩子结点作为下一层的根节点 继续去重复这个过程
	}
	h[k] = tmp; //最终的位置进行交换 （被筛选的结点值放入最终位置）
}
 
 
 
//--------建堆-------------
void Buildheap(int len ) {  
	for (int i = len / 2; i > 0; i-- ) {
		Heapadjust(i, len);
	}
}
 
 
 
//-------实现堆排序------------
void Heapsort(int len) {
	Buildheap(len);//初始建堆
 
	for (int i = len; i > 1; i--) { //n-1趟的交换和建堆过程
		swap(h[i], h[1]);//和堆底元素交换
		Heapadjust(1, i - 1);//调整，把剩余的i-1个元素整理成堆
	}
 
}
 
 
 
 
int main() {
	cin >> n >> m; //n个元素 输出前m小的数
	for (int i = 1; i <= n; i++) cin >> h[i];
	Buildheap(n);
	for (int i = 1; i <= n; i++) cout << h[i] << " ";
	cout << "\n";
	Heapsort(n);
	for (int i = 1; i <= m; i++) cout << h[i];
 
}

或者

可以使用c++函数make_heap(ve.begin(),ve.end(),less<int>() )
less<int>()对应大根堆 greater<int>()对应小根堆

#include <bits/stdc++.h>
using namespace std;
vector<int>h;
int n;
 
 
 
int main() {
	cin >> n;
	h.resize(n);
	for (int i = 0; i < n; i++) cin >> h[i];
	vector<int>a;
	a = h;
	make_heap(h.begin(), h.end()); //建立大根堆
	cout << h[0];
	for (int i = 1; i < n; i++) cout << " " << h[i];
	cout << endl;
	make_heap(a.begin(), a.end(), greater<int>());//建立小根堆
	cout << a[0];
	for (int i = 1; i < n; i++) cout << " " << a[i];
 
}