数据结构

顺序表

线性表的顺序表示

顺序表的定义

$1$.线性表的 顺序存储又称为 顺序表。
它是一组用地址连续的存储单元依次存储线性表中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也相邻。

$2$.顺序表的特点：表中元素的逻辑顺序与其存储的物理顺序相同。
线性表的顺序存储结构是一种随机存取的存储结构
通常用数组来描述线性表的顺序存储结构
线性表中的元素位序从1开始，数组下标从0开始。
一维数组可以静态分配，也可以动态分配。

$3$.顺序表的主要优点和缺点
优点：$a$.可进行随机访问。即可通过首地址和元素序号可以在O（1）时间内找到指定的元素。

$b$.存储密度高。每个结点只存储数据元素。
缺点：$a$.元素的插入和删除需要移动大量的元素。
$b$.顺序存储分配需要一段连续的存储空间，不够灵活。

易错题

$1.顺序表可以利用一维数组表示，因此顺序表与一维数组在逻辑结构上是相同的。（×）$

解释：顺序表是顺序存储的线性表，表中所有元素的类型必须相同，且必须连续存放。一维数组中的元素可以不连续存放（动态分配内存，可能会在堆内存中找到足够大的空闲块来存储数组，而这些空闲块可能是不连续的）。此外,栈、队列、和树等逻辑结构也可以利用一维数组表示，但它与顺序表不属于相同的逻辑结构。

$2.顺序表和一维数组一样，都可以进行随机存取(√)$

解释：随机存取指的是当存储器中的数据被读取或写入的时候，所需要的时间与该数据所在的物理地址无关。

$3.若长度为n的非空线性表采用顺序存储结构，在表的第i个位置插入一个数据元素，则i的合法值应该为1\le i \le n (×)$

解释：线性表元素的序号从1开始，而在第n+1个位置插入相当于在表尾追加。1<=i<=n+1才对。

顺序表上基本操作的实现

顺序表的实现--静态分配


#include <stdio.h> 
#define MaxSize 10
typedef struct{
	ElemType data[MaxSize];//ElemType是你要使用的对应类型比如int，double 
	int length;	//顺序表当前长度 
}SqList; //顺序表类型定义 





//基本操作--初始化一个顺序表 
void InitList(Sqlist &L)
{
	for(int i=0;i<MaxSize;i++)
	{
		L.data[i]=0;//将所有数据元素设置为0 
	}
	L.length=0;
 } 
 
 int main(){
 	SqList L;//声明一个顺序表 
 	InitList(L);//初始化顺序表
	 //....后续操作
	 return 0; 
 }

顺序表的实现--动态分配

#include <stdlib.h>
#include <stdio.h> 
#define InitSize 10
typedef struct{
	int length;
	int *data;
	int MaxSize;
}SeqList; //顺序表类型定义 


void InitList(SeqList &L)
{
	//使用malloc函数申请一段连续的存储空间 
	L.data=(int*)malloc(sizeof(int)*InitSize);
	 L.MaxSize=InitSize;
	 L.length=0;
}

void IncreaseSize(SeqList &L,int len)
{
	int *p=L.data;//将L原来的地址赋值给指针p 
	L.data=(int*)malloc(sizeof(int)*(L.MaxSize+len));//申请了一块新的地址 
	for(int i=0;i<L.length;i++) L.data[i]=p[i];//将数据复制到新区域
	L.MaxSize=L.MaxSize+len; 
	free(p);
}

int main()
{
	SeqList L;
	InitList(L);//初始化顺序表
	//...其他操作
	IncreaseSize(L,5);
	return 0; 
	
}

顺序表的实现--插入 复杂度$O(n)$

#include <stdlib.h>
#include <stdio.h> 
#define MaxSize 10
typedef struct{
	int data[MaxSize];
	int length;
}SqList; //顺序表类型定义 

void ListInsert(SqList &L,int i,int e)
{
	//一开始元素从0-length-1，所以这里相当于把i后面的元素都往后挪了一个位置 
	for(int j=L.length;j>=i;j--)
	{
		L.data[j]=L.data[j-1]; 
	}
	L.data[i-1]=e;
	L.length++; 
}


int main()
{
	SqList L;
	InitList(L);//初始化顺序表
	//...其他操作
	ListInsert(L,3,3);
	return 0; 
	
}

但是，通常我们会将插入操作的代码进行这样的优化，从而更好的执行。

bool ListInsert(SqList &L,int i,int e)
{
	if(i<=1||i>L.length+1) return false;//判断i的范围是否有效 
	if(L.length>=MaxSize) return false; //存储空间已满，无法插入 
	for(int j=L.length;j>=i;j--)
	{
		L.data[j]=L.data[j-1];
	}
	L.data[i-1]=e;//在i的位置放e 
	L.length++;//线性表长度+1 
	return true;
}

顺序表的实现--删除复杂度$O(n)$

bool ListDelete(SqList &L,int i,int &e)
{
	if(i<=1||i>L.length+1) return false;//判断i的范围是否有效 
	e=L.data[i-1];//将被删除的元素赋值给e 
	if(L.length>=MaxSize) return false; //存储空间已满，无法插入 
	for(int j=i;j<L.length;j++)
	{
		L.data[j-1]=L.data[j];
	}

	L.length--;//线性表长度-1
	return true;
} 


int main()
{
	SqList L;
	InitList(L);//初始化顺序表
	int e=-1;
	if(ListDelete(L,3,e))
		printf("已删除第3个元素，删除元素值为=%d\n",e);
	else 
		printf("位序i不合法，删除失败\n");
	return 0; 
	
}

练习题

综合应用题
$1.从顺序表中删除具有最小值的元素（假设唯一）并由函数返回被删元素的值，空出的位置由$ $最后一个元素填补，若顺序表为空，则显示出错信息并退出运行。$

$2.设计一个高效算法，将顺序表L的所有元素逆置，要求算法的空间复杂度为O(1)$$(算法执行过程中仅需要固定大小的额外空间。无论输入规模大小，所需的额外空间保持不变)。$

$3.对长度为n的顺序表L，编写一个时间复杂度为O(n)、空间复杂度为O(1)的算法，该算法删除$
$顺序表中所有值为x的数据元素。$

$4.从顺序表中删除其值在给定值s和t之间（包含s和t，要求s<t）的所有元素，若s或t不合理$
$或顺序表为空，则显示出错信息并退出运行。$

$5.从有序顺序表中删除所有重复的元素，使表中所有的元素的值均不相同。$

$6.从两个有序顺序表合并为一个新的有序顺序表，并由函数返回结果顺序表。$

$7.已知在一维数组A[m+n]里面一次存放两个线性表(a_1,a_2,...,a_m)和(b_1,b_2,...,b_m)$$。编写一个函数，将数组中的两个顺序表的位置互换，即将(b_1,b_2,...,b_m)放在(a_1,a_2,...,a_m)面前。$

$8.线性表(a_1,a_2,...,a_n)中的元素递增有序且按顺序存储于计算机内。要求设计一个算法，$$完成用最少时间在表中查找数值为x的元素，若找到，则将其与后继元素位置相交换，若找不到$$，则将其插入表中并使表中的元素仍递增有序$

$9.给定三个序列A,B,C,长度均为n，且均无重复元素的递增序列，请设计一个时间上尽可能$
$高效的算法，逐行输出同时存在于这三个序列中的所有元素。例如数组A为\{1，2，3\}，$
$数组B为\{2,3,4\},数组C为\{-1，0，2\},则输出2。要求：$
$1):给出算法的基本设计思想$
$2):根据设计思想，采用C语言或C++描述算法，关键之处给出注释。$
$3):说明算法的时间复杂度和空间复杂度。$

$10.【2010统考真题】，设将n(n>1)个整数存放到一维数组R中。设计一个在时间和空间都可能$
$高效的算法。将R中保存的序列循环左移p(0<p<n)个位置，即将R中的数据由(X_0,X_1,...,X_n-1)$$变换为(X_p,X_p+1,...,X_n-1,X_0,X_1,...,X_p-1)。要求：$
$1):给出算法的基本思想$
$2):根据设计思想，采用C语言或C++描述算法，关键之处给出注释。$
$3):说明算法的时间复杂度和空间复杂度。$

$11.【2011统考真题】，一个长度为L(L>=1)的升序序列S，处在第L/2(向上取整)个位置的数成为S的中位数。$$例如，若序列S_1=(11,13,15,17,19),则S_1的中位数为15，两个序列的中位数是含它们$$所有元素的升序序列的中位数。例如，若S_2=(2,4,6,8,20),则S_1和S_2的中位数是11。$$现在有两个等长升序序列A和B。设计一个高效的算法，找出A和B的中位数。$

$1):给出算法的基本思想$
$2):根据设计思想，采用C语言或C++描述算法，关键之处给出注释。$
$3):说明算法的时间复杂度和空间复杂度。$

$12.【2013统考真题】已知一个整数序列A=(a_0,a_1,...,a_n-1)，其中0<=a_i<n(0<=i<n)$
$若存在a_{p1}=a_{p2}=...=a_{pm}=x且m>n/2(0<=p_k<=n,1<=k<=m),则称x为A的主元素。$
$例如A=(0,5,5,3,5,7,5,5)则5为主元素；又如A=(0,5,5,3,5,1,5,7)，则A中没有主元素$
$假设A中的n个元素保存在一个一维数组中，请设计一个高效的算法找出A的主元素并输出，若不存在输出-1。$
$1):给出算法的基本思想$
$2):根据设计思想，采用C语言或C++描述算法，关键之处给出注释。$
$3):说明算法的时间复杂度和空间复杂度。$

$13.【2018统考真题】给定一个含n(n>=1)个整数的数组，设计一个高效算法，找出数组中未出现的$$最小正整数，例如，\{-5，3,2,3\}中未出现的最小正整数为1;\{1,2,3\}为4。$
$1):给出算法的基本思想$
$2):根据设计思想，采用C语言或C++描述算法，关键之处给出注释。$
$3):说明算法的时间复杂度和空间复杂度。$

答案

$1.$算法思想：遍历整个线性表，查找最小值并标记其位置，空出的位置由最后一个元素来填补。

bool Del_min(SqList &L,int &val)
{
	if(L.length==0) return false;//如果顺序表为空，返回错误 
	val=L.data[0];//假设0号位置最小 
	int pos=0;
	for(int i=1;i<L.length;i++)//循环找最小值 
	{
		if(L.data[i]<val)
		{
			pos=i;
			val=L.data[i];
		}
	}
	L.data[pos]=L.data[L.length-1];//空出的位置由最后一个元素填补 
	L.length--;
	return true;
	
}

$2.$算法思想：将前$L.length/2$的元素$L[i]$与$L.length/2$的元素$L[L.length-i-1]$交换。

void Reverse(SqList &L)
{
	int temp=0;
	for(int i=0;i<L.length/2;i++)
	{
		temp=L.data[i];
		L.data[i]=L.data[L.length-i-1];
		L.data[L.length-i-1]=temp;
	}
	
}

$3.$算法思想：令$pos=0$,遍历$L$，当遇到一个不为x的元素，便让$L[pos]$赋值为该元素，并让$pos+1$,遍历结束后，修改$L$的长度为$pos$

void Del_elm(SqList &L,int x)//记得传参进去，别老丢三落四的 
{
	int pos=0;
	for(int i=0;i<L.length;i++)
	{
		if(L.data[i]!=x) L.data[pos++]=L.data[i];
	}
	L.length=pos;//别忘记最后一步，改长度 
	
}

$4.$算法思想：遍历整个顺序表，遇到小于s或者大于t的元素时，就令L.data[k]为当前元素值,并更新k。

bool Del_elem(SqList &L,int s,int t)
{
	if(L.length==0||s>=t) return false;
	int pos=0;
	for(int i=0;i<L.length;i++)
	{
		if(L.data[i]<s||L.data[i]>t)
		{
			L.data[pos]=L.data[i];
			pos++;
		}
	}
	L.length=pos+1; 
	return true;
}

$5.$算法思想：由于是有序的顺序表，所以值相同的元素，一定在连续的位置上，所以第二个元素开始遍历顺序表，若当前元素与上一个元素不同，则令$L.data[k]$等于当前元素值，并更新$k$

void Del_same(SqList &L)
{
	int k=1;
	for(int i=1;i<L.length;i++)
	{
		if(L.data[i]!=L.data[i-1]){
			L.data[k]=L.data[i];
			k++;
		}
	}
	L.length=k;
}

$6.$算法思想：先处理两个顺序表中较短的部分，两两比较，将小者存入顺序表，再处理剩余的部分，将剩下部分加到顺序表后面。

bool merge(SqList &A,SqList &B,SqList &C)
{
	if(A.length+B.length>C.maxsize) return 0;
	
	int i=0,j=0,k=0;
	while(i<A.length&&j<B.length)//两两比较，小者存入顺序表C 
	{//记住是i j都在更新，所以可以达到排列前面共同部分所有元素的目的 
		if(A.data[i]<=B.data[j])//是<= 
		{
			C.data[k++]=A.data[i++];
		}else{
			C.data[k++]=B.data[j++];
		}
	}
	//处理剩余的部分 
	while(i<A.length) C.data[k++]=A.data[i++];
	while(j<B.length) C.data[k++]=B.data[j++];
	C.length=k;//更改C的长度 
	return 1; 
}

$6$.算法思想：先对整个数组进行翻转，然后对下标为$0到n-1$的元素进行翻转，再对$n到m+n-1$的元素进行翻转即可。

void  Reverse(int L[],int left,int right,int len)
{//left为左边起始下标，right为终止下标，len为整个数组长度 
	if(left>=right||right>=len) return ; 
	//传入的参数不合法就return 
	int l=left,r=right;
	int mid=(l+r)/2;
	for(int i=0;i<=mid-l;i++)//i相当于左右下标移动次数 
	{
		int temp=L[l+i];
		L[l+i]=L[r-i];
		L[r-i]=temp;
	}
	
}

void Exchange(int L[],int left,int right,int len)
{
	Reverse(L,0,m+n-1,len);//后面第四个填的是整个数组的长度，而非区间的长度 
	Reverse(L,0,n-1,len);
	Reverse(L,n,m+n-1,len);
}

$8.$算法思想：使用二分查找节省时间，若找不到则插入x。

void FindInsert_x(int x,int A[])
{
	int l=0,r=n-1;
	int mid=0;//二分 
	while(l<=r)//记住等号不能丢了
	{	 
		mid=(l+r)/2;
		if(A[mid]==x) break;
		else if(A[mid]<x){
			l=mid+1;
		}else {
			r=mid-1;
		}

	} 
	//两个if只会执行一个 
	if(A[mid]==x){
		int temp=A[mid];
		A[mid]=A[mid+1];
		A[mid+1]=temp;
	}
	
	//没找到x 
	if(l>r) //自己模拟一遍，不符合时l一定会大于r
	//当x大于数组最大值，r==n-1,l==n，数组相当于没挪动for循环不会执行，在最后插入x 
	//当x小于数组最小值r==-1,l=0; 数组相当于整体往后挪，在最前面插入x 
	{	int i;
	//i==n-1
		for( i=n-1;i>r;i--) A[i+1]=A[i];//把元素往后挪一位
		A[i+1]=x;//插入x 
	}

}

$9.$算法思想：使用三个下标变量遍历数组，当三个变量指向的值相等时，输出并向前推进指针，如果不同找出三个值的最大值，只推进小于最大值的元素的下标，直到某个下标变量移出数组范围即可停止。

void print_x(int A[],int B[],int C[])
{
	int i=0,j=0,k=0;//定义三个工作指针 
	while(i<n&&j<n&&k<n){
	if(A[i]==B[j]&&B[j]==C[k])//相同则输出，并集体向后移动 
	{
		cout<<A[i]<<endl;
		i++,j++,k++;		
	}
	else{
		int maxx=max({A[i],B[j],C[k]});
		while(A[i]<maxx) i++;
		while(B[j]<maxx) j++;
		while(C[k]<maxx) k++;
	}
	}
}

时间复杂度为$O(n),$因为只使用了常数个变量，所以空间复杂度为$O(1)$。

$10.$算法思想：先对元素进行整体翻转，再进行局部的翻转，就可以达到循环左移的目的。

void Reverse(int A[],int left,int right)
{
	int l=left,r=right,mid;
	mid=(left+right)/2;
	for(int i=0;i<=mid-left;i++) //交换元素位置,实现翻转 
	{
		int temp=A[l+i];
		A[l+i]=A[r-i];
		A[r-i]=temp;
	}
	
}

void move_array(int A[],int p,int n)
{
	Reverse(A,0,n-1);
	Reverse(A,0,n-p-1);
	Reverse(A,n-p-1,n-1);
	
}

时间复杂度$O(n)$，空间复杂度$O(1)$。

$11.$算法思想：从小到大遍历$A$和$B$中的元素，当访问到第$n$个值时即为两个数组的中位数

void find_mid(int a[],int b[],int n)
{
	int i=0,j=0,k=0,ans;
	while(i<n&&j<n)
	{
		if(a[i]<b[j])
		{
			ans=a[i];
			i++;
		}else{
			ans=b[j];
			j++;
		}
		
		if(k==n) {
			cout<<ans;
			break;
		}
		k++;
		//cout<<i<<" "<<j<<" "<<k<<endl;
	}
	if(i==n&&j==0) cout<<b[j];
	if(j==n&&i==0) cout<<a[i];
}

时间复杂度为$O(n)$,空间复杂度为$O(1)$。

$12.$算法思想：先选取候选主元素。遍历所有元素，令第一个整数为$temp$，记录$temp$出现次数为1；若下一个元素仍为$temp$则计数+1，否则计数-1；当计数到0时将遇到的下一个元素保存到$temp$，计数重新记为1，开始下一轮计数，直至扫描完所有元素，最后判断$temp$是否为真的主元素。统计$temp$的次数，若大于$n/2$，则为主元素。

int find_major(int a[])
{
	int cnt=1,temp=a[0];//temp用来保存候选主元素，cnt用来计数 
	for(int i=1;i<n;i++)
	{
		if(a[i]==temp)
		{
			cnt++;//对A中的主元素计数 
		}else{
			if(cnt>0) cnt--;//处理不是主元素的情况 
			else{
				cnt=1;
				temp=a[i];//更换主元素 
			}
		}
	}
	
	if(cnt>0)
	{
		cnt=0;
		for(int i=0;i<n;i++) if(a[i]==temp) cnt++;//统计候选主元素出现次数 
	}
	if(cnt>n/2) return temp;//确认候选主元素 
	return -1;
	
}

时间复杂度为$O(n)$,空间复杂度为$O(1)$

$13.$算法思想：使用一个标记数组$mark$，大小为$n$，初始化每个元素为$0$，然后遍历A数组，当$1<=A[i]<=n$时,标记$mark[A[i]-1]=1$，随后遍历标记数组，遇到第一个不为1的元素跳出循环，返回$i+1$，若都为1，此时$i=n-1$，还是返回$i+1$，刚好为$n$ 。

int find_mex(int A[])
{
	int i,*mark;//mark为标记数组 
	mark=(int *)malloc(sizeof(int )*n);//分配空间 
	memset(mark,0,sizeof mark);//将mark数组初始化为0 
	for(int i=0;i<n;i++)
	{
		if(A[i]>0&&A[i]<=n) mark[A[i]-1]=1;
	}
	int i;
	for(i=0;i<n;i++){//扫描找到目标值
		if(mark[i]==0) {
			break;
		}
	}
	return i+1;
}

时间复杂度为$O(n)$,因为额外分配了$mark[n]$,所以空间复杂度为$O(n)$;

线性表的链式表示

单链表的定义

线性表的链式存储又称为单链表，它是指通过任意一组任意的存储单元来存储线性表中的数据元素。

由于单链表的元素离散地分布在存储空间中，因此是非随机存取的存储结构，即不可以直接找到表中某个特定的点。查找特定结点时，需要从表头开始遍历，依次查找。

通常用头指针L来表示一个单链表，指出链表的起始地址，头指针为NULL时表示一个空表。
此外，为了操作上的方便，在单链表第一个数据结点之前附加一个结点，称为头结点。

头结点和头指针的关系：不管带不带头结点，头指针都始终指向链表的第一个结点，而头结点是带头结点的链表中的第一个结点，结点内通常不存储信息。

引入头结点后，可以带来两个优点：

由于第一个数据结点的位置被存放在头结点的指针域中，因此在链表的第一个位置上的操作和在表的其他位置上的操作一致，无需进行特殊处理。
无论链表是否为空，其头指针都是指向头结点的非空指针（空表中头结点的指针域为空），因此空表和非空表的处理也得到了统一。

单链表上基础操作的实现

单链表的插入删除

#include <bits/stdc++.h>
using namespace std;
typedef struct Lnode{
	int data;
	struct Lnode *next;
}Lnode,*Linklist;

//链表的初始化
bool InitList(Linklist &L)//初始化带头结点的链表 
{
	L=(Lnode*)malloc(sizeof (Lnode));//创建头结点 
	L->next=NULL;//头结点之后暂时没有元素结点 
	return true;
}

bool IniList(Linklist &L)//初始化不带头结点的链表 
{
	L=NULL;
	return true;
}

//链表的按序插入操作 O（1）
bool Listinsert(Linklist &L,int e,int i)
{
	if(i<1) return false ;
	Lnode *p;
	int j=0;//让p挪到第i-1个结点
	p=L;
	while(p!=NULL&&j<i-1) 
	{
		p=p->next;
		j++;
	}
	if(p==NULL) return false;
	Lnode *s=(Lnode*)malloc(sizeof (Lnode) );
	s->data=e;
	s->next=p->next;
	p->next=s;
	return true;
} 

//链表的指定结点的后插操作 
bool Insertnextnode(Lnode *p,int e)
{
	if(p==NULL) return false ;
	Lnode *s=(Lnode *) malloc(sizeof (Lnode));
	s->data=e;
	s->next=p->next;
	p->next=s; 
	return  true; 
}


//链表的指定结点的前插操作
bool Insertpriornode(Lnode *p,int e)
{
	if(p==NULL) return false;
	Lnode *s=(Lnode*)malloc(sizeof (Lnode));
	 s->next=p->next;
	 p->next=s;
	 s->data=p->data;
	p->data=e;
	return true;
} 
//或者传入头指针
 bool Insertpriornode(Lnode *p,int e,Linklist L)

//按位序删除(带头结点) 
bool Listdelete(Linklist &L,int e,int i) 
{
	if(i<1) return false;
	Lnode *p;
	p=L;
	int j=0;
	while(p!=NULL&&j<i-1)
	{
		p=p->next;
		j++;
	}
	
	Lnode *q=p->next;
	e=q->data;
	p->next=q->next;
	free(q);
	return true;
}

//指定结点的删除 (不能删最后一个)
bool Deletenode(Lnode *p)
{
	//原理是把下一个值赋值到当前这个值，然后释放下一个的地址 
	if(p==NULL) return false;
	Lnode *q=p->next; 
	p->data=p->next->data;
	p->next=q->next;
	free(q); 
	return true;
}

单链表的查找

//按位查找 ,返回第i个元素(带头结点) O(n)
Lnode *getelem(Linklist &L,int i)
{
	if(i<0) return NULL;//这里是NULL，别写出false 
	int j=0;
	Lnode *p;
	p=L;
	while(p!=NULL&&j<i){
		j++;
		p=p->next;
	}
	return p;
}


//按值查找,找到数据域==e的结点 O(n)

Lnode *findelme(Linklist L,int e) 
{
	Lnode *p=L->next;
	//从第1个结点开始查找 
	while(p!=NULL&&p->data!=e)
	{
		p=p->next;
	}
	return p;
}

//求链表的长度O(n)
int Length(Linklist L) 
{
	int len=0;
	Lnode *p=L;
	while(p->next!=NULL)
	{
		p=p->next;
		len++;
	}
	return len;
}

单链表的建立

#include <bits/stdc++.h>
#define int long long
using namespace std;

typedef struct Lnode{
	int data;
	struct Lnode *next;
}Lnode ,*Linklist;


//尾插法建立单链表 
Linklist Inserttail(Linklist &L)
{
	int x;
	 L=(Linklist)malloc(sizeof (Lnode));//建立头结点 
	Lnode *s,*r=L;//r为表尾指针 
	cin>>x;
	while(x!=9999)
	{
	 s=(Lnode*)malloc(sizeof (Lnode));
		s->data=x;
		r->next=s;
		r=s;	//r指向新的表尾结点 
		cin>>x;
	}
	r->next=NULL;//尾结点置空 
	return L; 
}

//头插法建立单链表，每次在头结点后面插入，而不是一直在尾部插入 
Linklist Inserthead(Linklist &L)//注意返回值类型 
{
	int x;
	 L=(Linklist)malloc(sizeof (Lnode));//创建头结点 
	L->next=NULL;//好习惯给它写上,初始为空链表 
	Lnode *s;
	cin>>x; 
	while(x!=9999)
	{
		s=(Lnode*)malloc(sizeof (Lnode));
		s->next=L->next;
		s->data=x;
		L->next=s;
		cin>>x;
	}
	
	return L;
 } 

signed main()
{
	return 0;
}

双链表

#include <bits/stdc++.h>
#define int long long
using namespace std;
//双链表的结点类型 
typedef struct Dnode{
	int data;
	struct Dnode *prior,*next;
}Dnode ,*Dlinklist;

//双链表的初始化 
bool Inidlinklist(Dlinklist &L)
{
	L=(Dnode*)malloc(sizeof(Dnode));
	if(L==NULL)  return false;
	L->prior=NULL;
	L->next=NULL;
	return true;
}

//在p结点之后插入s结点 
bool Insertnextdnode(Dnode *p,Dnode *s)
{
	if(p==NULL||s==NULL) return false;
	s->next=p->next;
	if(p->next!=NULL){
		p->next->prior=s;
	} 
	s->prior=p;
	p->next=s;
	
}

//双链表的删除 
bool Deletenextnode(Dnode *p)
{
	if(p==NULL) return false;
	Dnode *q=p->next;
	if(q==NULL) return false;
	p->next=q->next;
	if(q->next!=NULL) q->next->prior=p;
	free(q);
	return true;
	
}

void test()
{
	Dlinklist L;
	Inidlinklist(L);
}


signed main()
{
	return 0;
}

循环链表

1.循环单链表
循环单链表和单链表的区别在于，表中的最后一个结点不是NULL，而改为指向头结点，从而整个链表形成一个环。

在循环单链表中，表尾结点的*r的next域指向L，故表中没有指针域为NULL的结点，因此循环单链表的判空条件不是头结点的指针是否为空，而是它是否等于头指针L。

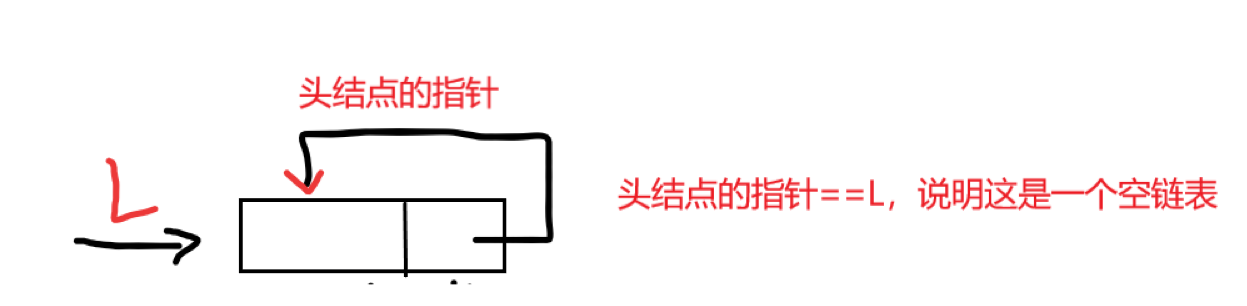
在单链表中只能从表头结点开始往后顺序遍历整个链表，而循环单链表可以从表中的任意一个结点开始遍历整个链表。
有时对循环单链表不设头指针而仅设尾指针，以使得操作效率更高。其原因是，若设的是头指针，对在表尾插入元素需要$O(n)$的复杂度，若设的是尾指针r，r->next即为头指针，对在表头和表尾插入元素都只需要$O(1)$的复杂度。

2.循环双链表
由单链表的定义不难找出循环双链表。不同的是，在循环双链表中，头结点的prior指针还要指向表尾结点。

当循环链表为空表时，其头结点的piror域和next域都等于L

静态链表

静态链表是用数组来描述线性表的的链式存储结构，结点有数据域data和指针域next，与前面所讲的指针不同的是，这里的指针是结点在数组中的相对地址(数组下标），又称游标。和顺序表一样，静态链表也要预先分配一块连续的内存空间。

//静态链表
#define Maxsize 50
typedef struct{
	int data;
	int next
}Slinklist[Maxsize];

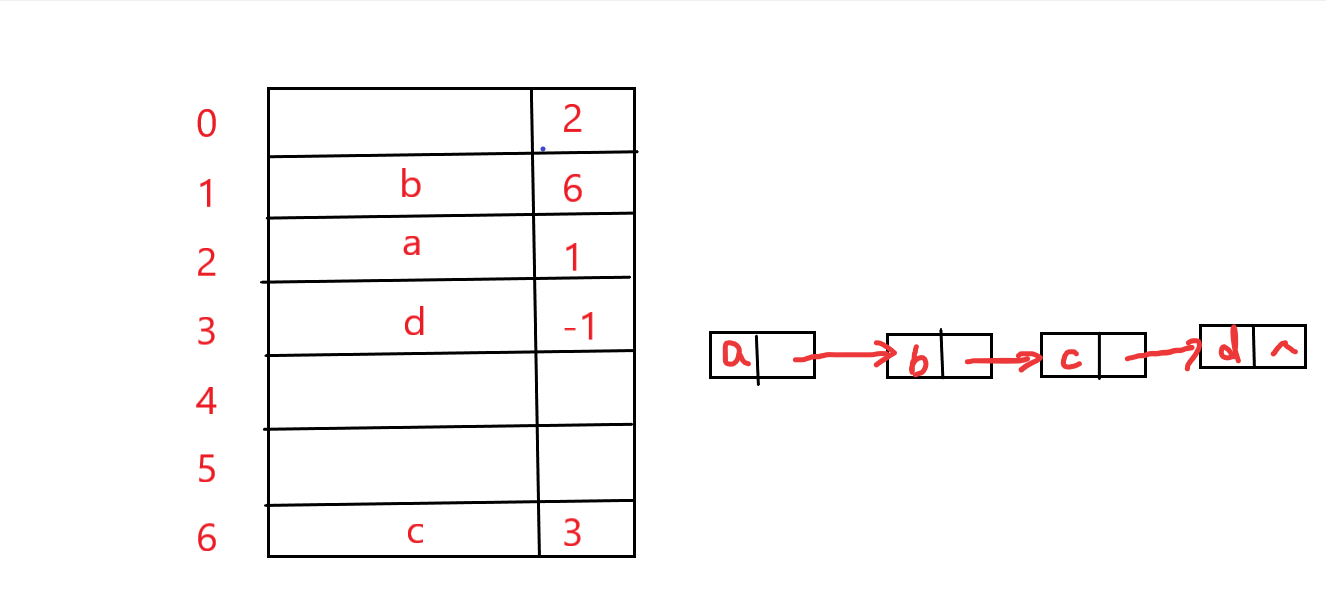
静态链表以next==-1作为其结束的标志。静态链表的插入、删除操作与动态链表的相同，只需要修改指针，而不需要移动元素。

顺序表和链表的比较

1.存取方式
顺序表可以顺序存取，也可以随机存取，链表只能从表头开始依次顺序存取。例如在第i个位置上执行存取的操作，顺序表仅需依次访问，而链表需要从表头开始依次访问。

2.逻辑结构和物理结构
采用顺序存储时，逻辑上相邻的元素，对应的物理存储位置也相邻。而采用链式存取时，逻辑上相邻的元素，物理存储位置不一定相邻，对应的逻辑关系是通过指针链接来表示的。

3.查找、插入和删除操作
对于按值查找，顺序表无序时，两者的时间复杂度均为$O(n)$；顺序表有序时，可采用二分查找，此时的时间复杂度为$O(log_2n)$。对于按序号查找，顺序表支持随机访问，时间复杂度仅为$O(1)$，而链表的平均时间复杂度为$O(n)$。顺序表的插入删除操作，平均需要移动半个表长的元素。链表的插入删除操作，只需要修改相关结点的指针域即可。

练习题

易错题

$1.链式存储设计时，结点内的存储单元地址()$

\[A:一定连续\quad B：一定不连续\quad C:不一定连续\quad D：部分连续，部分不连续 \]

$2.给定有n个元素的一维数组，建立一个有序单链表的最低时间复杂度是()$

\[A.O(1)\quad B.O(n)\quad C.O(n^2)\quad D.(nlog_2n) \]

$3.将长度为n的单链表链接在长度为m的单链表后面，其算法的时间复杂度为()$

\[A.O(1)\quad B.O(n)\quad C.O(m)\quad D.(n+m) \]

$4.对于一个头指针为head的带头结点的单链表，判定该表为空表的条件是(),对于不带头结点$
$的单链表，判定为空表的条件为()$

\[A.head==NULL\quad B.head!=NULL\quad C.head->next==NULL\quad D.head->next==head \]

$5.对于一个带头结点的双循环链表L，判断该表为空表的条件是()$

\[A.头结点的指针域为空\quad B.L的值为NULL\quad C.头结点的指针域与L的值相等\quad D.头结点的指针域与L的地址相等 \]

$6.设有两个长度为n的循环单链表，若要求两个循环单链表的头尾相接的时间复杂度为O(1),则$
$则对应两个循环单链表各设置一个指针，分别指向()$

\[A.各自的头结点\quad B.各自的尾结点\quad C.各自的首结点\quad D.一个表的头结点，另一个表的尾结点 \]

$7.设有一个长度为n的循环单链表，若从表中删除首元结点的时间复杂度达到O(n),则此时采用的$$循环单链表的结构可能是()$

\[A.只有表头指针，没有头结点\quad B.只有表尾指针，没有头结点\quad C.只有表尾结点，带头结点\quad D.只有表头指针，带头结点 \]

$8.某线性表用带头结点的循环单链表存储，头指针为head，当head->next->next==head成立时，线性表的长度可能是()$

\[A.0\quad B.1\quad C.2\quad D.可能为0或1 \]

$9.需要分配较大空间，插入和删除不需要移动元素的线性表，其存储结构为()$

\[A.单链表\quad B.静态链表\quad C.顺序表\quad D.双链表 \]

$10.已知头指针h指向一个带头结点的非空单循环链表，p是尾指针，q是临时指针，现要删除该链表的第一个元素$$正确的语句序列是()$
$A.h->next=h->next->next;q=h->next;free(p)$
$B.q=h->next;h->next=h->next->next;free(q)$
$C.q=h->next;h->next=q->next;if(p!=q)p=h;free(q)$
$D.q=h->next;h->next=q->next;if(p==q)p=h;free(q)$

答案

A
解释：结点内存放的是数据域和指针域，所以存储单元地址一定连续。
D
解释：因为要得到有序单链表，如果先将数组排好序，数组排序的最低时间复杂度为$O(nlog_2n)$，然后建立这个链表的时间复杂度为$O(n)$,取更大的O。如果先建立链表，然后依次插入建立有序表，则每插入一个元素就需要遍历链表寻找插入位置，即直接插入排序，时间复杂度为$O(n^2)$
C
解释：虽然链表在尾部插入的时间复杂度为$O(1)$,但需要先遍历长度为m的链表找到尾结点，所以时间复杂度为$O(m)$。
B A
解释：带头结点的单链表判空条件为$head->next==NULL$，因为head指向头结点，头结点下一个结点若为空，则说明单链表为空。若不带头结点，则head指向第一个节点，若$head==NULL$，则说明表为空。
C
解释：带头结点循环单链表的判空条件为头结点的指针域与L的值相等。也就是头结点的指针指向了自己，说明没有下一个结点了，但是注意是与L的值相等，而不是与L的地址相等，因为L的值是这个头结点的地址，而L的地址，是指针在内存中的地址。
B
解释：因为没有说明哪个链表接在哪个链表的后面，所以两个临时指针各自指向各自的尾结点时，可以快速的通过尾指针找到头结点。
A
解释：删除首元结点，要找到一个前驱结点，如果有头结点，那么无论有没有表尾指针或者表头指针，删除的时间复杂度都为$O(1)$；如果没有头结点而有表头指针，由于这是一个循环单链表，最后一个结点指向的是头结点，所以我们需要先遍历整个链表去找到最后一个结点，然后通过表头指针和尾结点的指针域去删除首元结点；如果有表尾指针，没有头结点时，也可以$O(1)$的找到第一个结点。
D
解释：这一题要注意，不要把头结点也算成线性表的一部分，头结点只是为了方便运算，当只有一个头结点也就是线性表长度为0时，head后面无论有多少个next最后都会指向head，因为这是个循环单链表。当线性表长度为1时，头结点的下一个结点的指针域也就是$head->next->next$等于$head$时，说明指向了头结点，也是符合情况的。
B
解释：静态链表采用数组表示，因此需要预先分配较大的连续空间。
D
解释：首先要区分我们要删的是第一个元素，而不是头结点，当结点数大于2时，其实只需要把头结点的指针域指向第一个结点后的结点，然后释放第一个结点内存即可。但是考虑特殊情况，当只有一个元素结点时，要先把尾指针指向头结点，即$if(p==q)\quad p=h$，最后也是释放内存即可。

综合应用题

$1.在带头结点的单链表L中，删除所有值为x的结点，并释放其空间，假设值为x的结点不唯一$
$,试编写算法实现上述操作。$

$2.试编写在带头结点的单链表L中删除一个最小值结点的高效算法(假设该节点唯一)$

$3.试着编写算法将带头结点的单链表就地逆置，所谓就地就是指辅助空间复杂度为O(1)。$

$4.设在一个带表头结点的单链表中，所有结点的元素值无序，试编写一个函数，删除表中所有介于给定的两个值(作为函数参数给出)之间的元素(若存在)。$

$5.给定两个单链表，试分析找出两个链表的公共结点的思想(不用写代码)$

$6.设C=\{a_1,b_1,a_2,b_2,...,a_n,b_n\}为线性表，采用带头结点的单链表存放，设计一个$$就地算法，将其拆分为两个线性表，使得A=\{a_1,a_2...,a_n\}，B=\{b_1,b_2,...,b_n\}。$

$7.在一个递增有序的单链表中，存在重复的元素，设计算法删除重复的元素。$

$8.设A和B是两个单链表(带头结点)，其中元素递增有序。设计一个算法从A和B中的公共元素产生单链表C，要求不破坏A、B的结点。$

$9.已知两个链表代表A和B分别代表两个集合，其元素递增排序。编制函数，求A和B的交集，并存放于A链表中。$

$10.两个整数序列A=a_1,a_2,a_3,...,a_m和B=b_1,b_2,b_3,...,b_n已经存入两个单链表中，设计一个算法，判断序列B是否是序列A的连续子序列。$

$11.设计一个算法用于判断带头结点的循环双链表是否对称。$

$12.有两个循环单链表，链表头指针分别为h1和h2，编写一个函数将链表h2链接到链表h1之后，要求链接后的链表仍保持循环链表形式。$

$13.设有一个带头结点的非循环双链表L，其每个结点中除有pre、data、next域外，还有一个访问频度域freq，其值均初始化为0。$$每当在链表中进行一次Locate(L,x)运算时，令值为x的结点freq域的值增加1，并使此链表中的结点保持按访问频度递减的顺序排$$列，且最近访问的结点排在频度相同的结点之前，以便使频繁访问的结点总是靠近表头。试着编写符合上述要求的Locate(L,x)函数$$，返回找到结点的地址，类型为指针型。 $

$14.设将n(n>1)个整数存放到不带头结点的单链表L中，设计算法将L中保存的序列循环右$$移k(0<k<n)个位置。例如，k=1，则将链表{0,1,2,3}变为{3,0,1,2}。$
$1.给出算法的基本思想$
$2.根据设计思想，采用语言或描述算法，关键之处给出注释。$
$3.说明算法的时间复杂度和空间复杂度。$

$15.单链表有环，是指单链表的最后一个结点的指针指向了链表中的某个结点。$$试编写算法判断单链表是否存在环。$
$1.给出算法的基本思想$
$2.根据设计思想，采用语言或描述算法，关键之处给出注释。$
$3.说明算法的时间复杂度和空间复杂度。$

$16.设有一个长度为n(n为偶数)的不带头结点的单链表，且结点值都大于0，设计算法求这个单链$$表的最大孪生和。孪生和定义为一个结点值与其孪生结点值之和，对于第i个结点(从0开始)$$，其孪生结点为n-i-1个结点$
$1.给出算法的基本思想$
$2.根据设计思想，采用语言或描述算法，关键之处给出注释。$
$3.说明算法的时间复杂度和空间复杂度。$

$17.【2009统考真题】已知一个带有表头结点的单链表，假设这个链表只给出了头指针p，在不改$$变链表的前提下，请设计一个尽可能高效的算法，查找链表中倒数第k个位置上的结点。若查找$$成功输出该点data域的值，并返回1，否则只返回0.$
$1.给出算法的基本思想$
$2.根据设计思想，采用语言或描述算法，关键之处给出注释。$
$3.说明算法的时间复杂度和空间复杂度。$

$18.【2012统考真题】假定采用带头结点的单链表保存单词，当两个单词有相同的后缀的时，可享$$用相同的后缀存储空间，设str1和str2分别指向两个单词所在单链表的头结点，请设计一个时$$间上尽可能快的算法，找出str1和str2所指向两个链表共同后缀的起始位置。$
$1.给出算法的基本思想$
$2.根据设计思想，采用语言或描述算法，关键之处给出注释。$
$3.说明算法的时间复杂度和空间复杂度。$

$19.【2015统考真题】用单链表保存m个整数，结点的结构为[data][next],且|[data]|<n现要求设计$$一个尽可能高效的算法，对于链表中data的绝对值相等的结点，仅保留第一次出现的结点而删$$除其余绝对值相等的结点。$
$1.给出算法的基本思想$
$2.根据设计思想，采用语言或描述算法，关键之处给出注释。$
$3.说明算法的时间复杂度和空间复杂度。$

$20.【2019统考真题】设线性表L=(a_1,a_2,a_3,,...,a_n-2,a_n-1,a_n)采用带头结点的单链表保$$存，请设计一个空间复杂度为O(1)且时间上尽可能高效的算法，重新排列L中的各结点，得到线$$性表L'=(a_1,a_n,a_2,a_n-1,a_3,a_n-2,...)$
$1.给出算法的基本思想$
$2.根据设计思想，采用语言或描述算法，关键之处给出注释。$
$3.说明算法的时间复杂度和空间复杂度。$

答案
1.
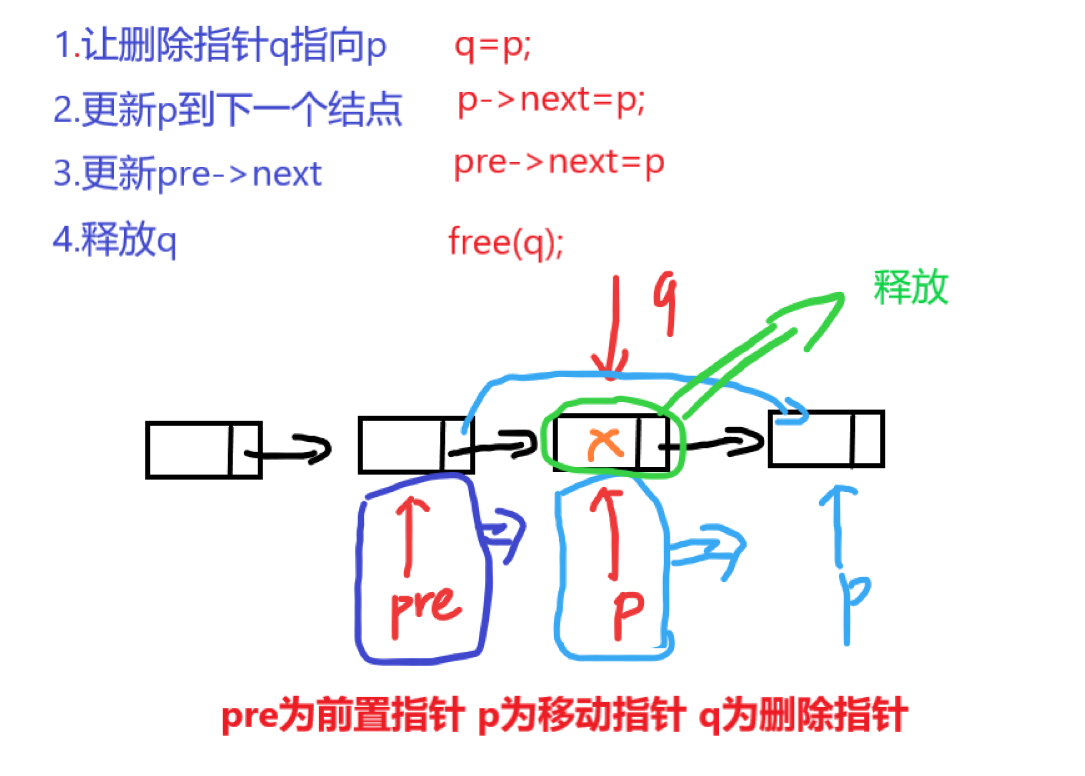
用p从头到尾扫描单链表，pre指向*p的前驱。若p所指结点的值为x，则删除，并让p移向下一个结点，否则pre和p同步往后移动一个结点。

void Deletex(Linklist &L,int x)
{
	Lnode *p=L->next,*pre=L,*q;//p为移动指针，pre为前置指针，q为删除指针
	while(p!=NULL)
	{
		if(p->data==x)
		{
			q=p;
			pre->next=p->next;
			p=p->next
			free(q);
		}else{
			pre=p;
			p=p->next;
		}
	}
	
}

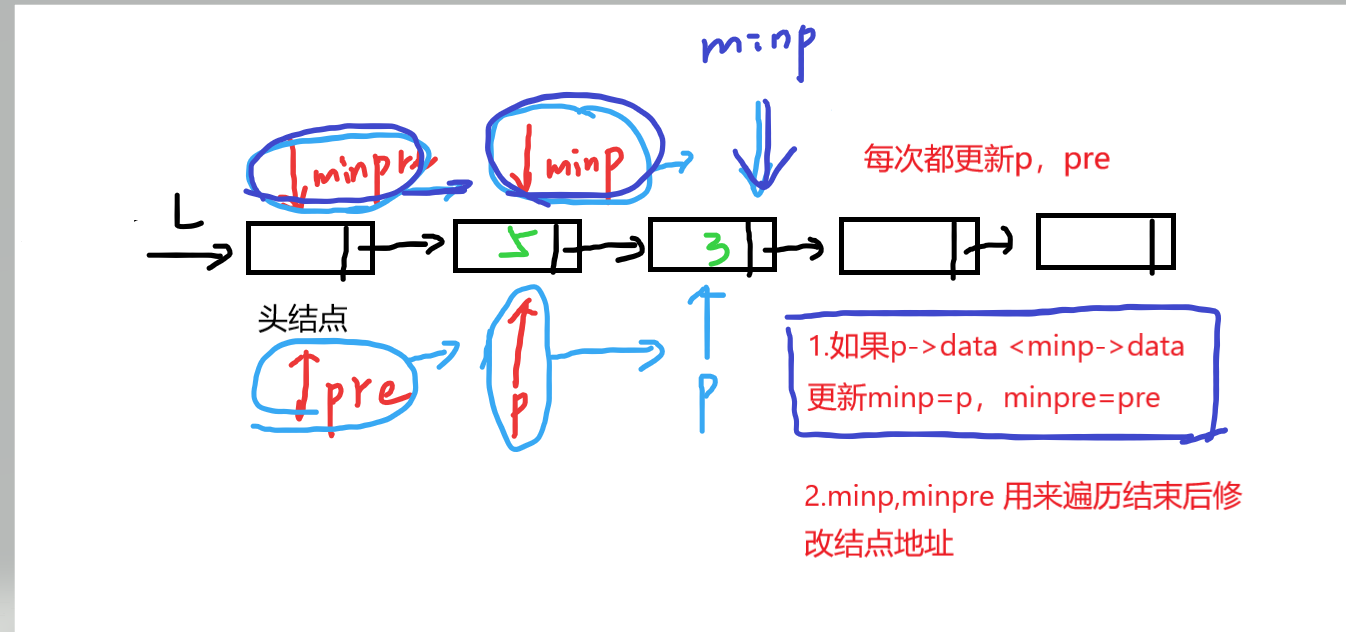
从p头到尾扫描单链表，若p的数据域小于当前minp所指的结点数据域，则更新minp和minpre直至遍历完整个链表，最后用minp和minpre删除minp指向的结点。

Linklist Deletemin(Linklist &L)//注意返回值
{
	Lnode *p=L->next,*pre->L;
	Lnode *minp=p,*minpre=pre;
	
	while(p!=NULL)
	{
		if(p->data<minp->data)
		{
			minp=p;
			minpre=pre;
		}
		pre=p;
		p=p->next;
	}
	
	minpre->next=minp->next;
	free(minp);
	return L;
}

解法1

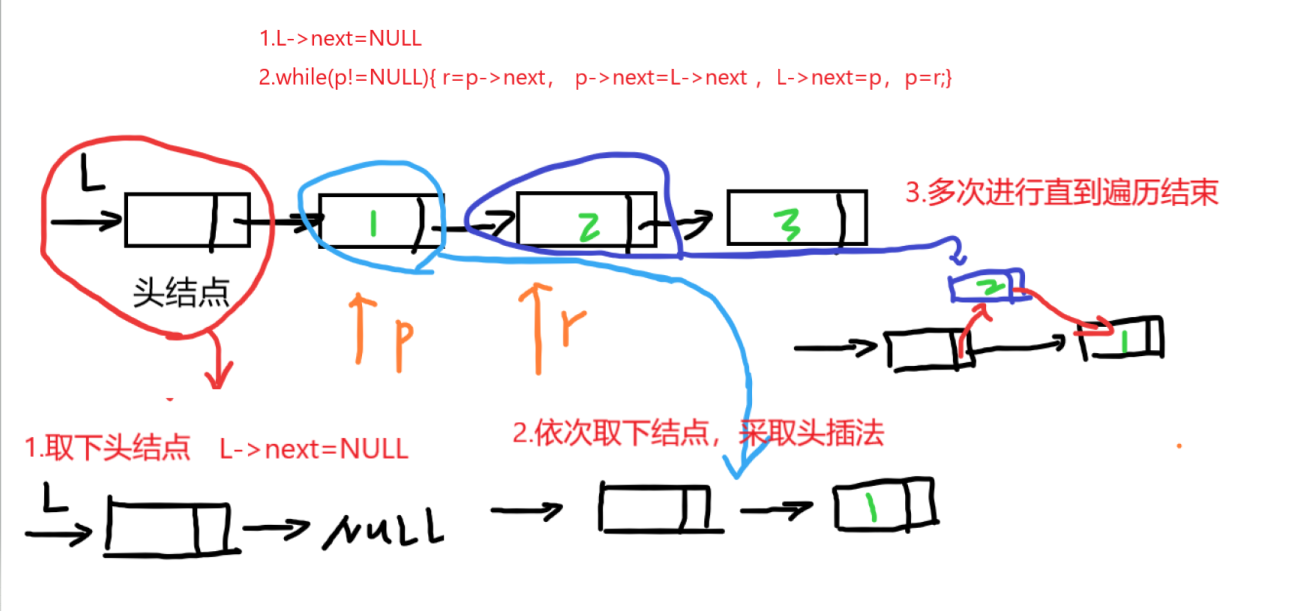
取下头结点以后，使用头插法依次取下每个结点。

Linklist Reverse(Linklist &L)
{
	Lnode *p,*r;
	p=L->next;
    L->next=NULL;//取下头结点 
  
	while(p!=NULL)
	{
		r=p->next;//后继指针，方便更新p 
		p->next=L->next;//头插法 
		L->next=p;
		p=r;
	}
	return L;
}

解法2

Linklist Reverse(Linklist &L)
{
	Lnode *pre,*p=L->next,*r;
	p->next=NULL;//处理第一个结点 
	while(r!=NULL)
	{
		pre=p; 
		p=r;
		r=r->next;
		p->next=pre;//处理中间的结点 
	}
	
	L->next=p;//处理最后一个结点 
	
}

4.逐个遍历检查，符合就删除。

void Delete_x(int a,int b,Linklist &L)
{
	Lnode *pre=L,*p=L->next;
	
	while(p!=NULL)
	{
		if(p->data>a and p->data<b)	 //找到则删除	
		{
			pre->next=p;
			free(p);
		}
		else{	//没找到继续找 
			pre=p;
		}

		p=p->next;
	}

}

5.两个单链表的公共结点，即两个链表从某一个结点开始，它们的next都指向同一结点。所以拓扑形状是Y型。
暴力的方法复杂度为$O(len1 * len2)$，即先遍历第一个链表，每遍历一个结点都在第二个链表中遍历一次，看能否找到相同的结点。
优化后的方法复杂度为$O(len1+len2)$，即先在长度较长的链表中，遍历长度之差个结点，然后在同时遍历两个链表，直至找到相同的结点。

先将线性表C整个存到链表A当中，然后对于奇数结点a采取尾插法，对于偶数结点b采取头插法。

Linklist Discreat(Linklist A)
{
	Lnode B=(Lnode *)malloc(sizeof (Lnode))//创建B的头结点 
	B->next=NULL;
	Lnode *ra=A, *p=A->next,*q;
	//ra始终指向A的尾结点 p为工作指针 q用来让p调整位置
	while(p!=NULL)
	{
		ra->next=p;//ra的指针域指向a的尾结点 
		ra=p;//此时p还在a的结点 
		p=p->next;//这一步p指向的是b的结点 
		if(p!=NULL)
		{
			q=p->next;//q指向a的结点
			p->next=B->next;
			B->next=p; 
			p=q;//p又指向a的结点 
		}
		
	 } 
	ra->next=NULL;
	return B;

}

pre为前置指针，p为工作指针，当出现重复元素的时候pre不更新，更新p，删除重复结点，当元素不重复时更新pre的位置为p的位置，直至遍历完单链表。

void Delete_same(Linklist &L)
{
	//题目默认有头结点 
	Lnode *pre=L,*p=L->next,*q;
	 while(p!=NULL)
	 {
		if(p->data==pre->data)
	 	{
	 		q=p;
			pre->next=p->next;
			p=p->next;
			free(q);
		}else{
			pre=p;
			p=p->next;
		}
	 	
	 }
	
}

8.因为链表递增有序，所以从第一个元素开始比较AB两表的元素，若元素值不等，则值小的指针往后移，若相等，创建一个等于该值的新结点，使用尾插法插入C中。

void get_common(Linklist &A,Linklist &B)
{
	Lnode *a=A->next,*b=B->next,*s,*r;
	//r始终指向C的尾结点 s用来申请结点 
	Lnode C=(Lnode *) malloc(sizeof (Lnode ));
	while(a!=NULL&&b!=NULL)
	{
		if(a->data<b->data)
		{
			a=a->next;
		}else if(a->data>b->data){
			b=b->next;
		}else{//找到公共元素结点 
			Lnode s=(Lnode *)malloc(sizeof (Lnode ));
			s->data=a->data;
			r->next=s;//尾插法 
			r=s;
			a=a->next;//继续移动ab指针 
			b=b->next;
		}
		
	}
	r->next=NULL;//把C的尾结点指针设置为空 
	
}

9.设置两个工作指针pa和pb，对两个链表进行归并并扫描，只有同时出现在两个集合终点元素才保留在链表A当中，否则释放该结点。当一个链表遍历完毕后，再释放剩下的结点。

Linklist  getCommon(Linklist &A,Linklist &B)
{
	Lnode *pa=A->next;
	Lnode *pb=B->next;
	Lnode *q,pre=A;//q为临时指针，指向释放内存的部分
	//pre为链表A 上的前置指针 
	
	while(pa&&pb)//这个while找公共元素，并将不是公共元素的释放掉 
	{
		if(pa->data==pb->data)
		{
			pa=pa->next;
			pre=pa;
			q=pb;
			pb=pb->next; 
			free(q);
		}
		else if(pa->data<pb->data)
		{
			q=pa;
			pa=pa->next;
			free(q);
		}else{
			q=pb;
			pb=pb->next;
			free(q);
		}
	 } 
	
	//继续释放那些不是公共元素的链表块 
	while(pa)
	{
		q=pa;
		pa=pa->next;
		free(q);
	}
	
	while(pb)
	{
		q=pb;
		pb=pb->next;
		free(q);
	}
	
	pa->next=NULL;
	free(pb);//记得释放掉B的头结点 
	return A;
}

10.扫描链表B，并且在链表A中确认当前结点是否与之匹配，如果不匹配更新A的指针，如果匹配同时更新A、B的指针，最后确认是否链表B被扫描完毕即可。

bool Ispattern(Linklist A,Linklist B)
{
	Lnode pa=A->next;
	Lnode pb=B->next;
	
	while(pb&&pb)
	{
		if(pa->data==pb->data)
		{
			pa=pa->next;
			pb=pb->next;
		}else{
			pa=pa->next;
		}
		
	}
	
	if(pb==NULL) return true;
	else return false;
	
 }

11.让p指针从第一个元素结点开始扫描，q从尾结点开始扫描，如果结点元素值相同则都更新，否则返回错误。

bool Issymmetry(Linklist L)
{
	Lnode p=L->next;
	Lnode q=L->piror;
	while(q!=p&&p->next!=q) //左边为结点数为奇数的终止条件，右边为偶数 
	{
		if(p->data==q->data)
		{
			p=p->next;
			q=q->piror;	
		}else{
			return false;
		}	
		
	} 
	
	return true;
}

12.使用工作指针pa、pb遍历到最后一个结点，然后将第一个链表的尾指针指向第二个链表的头指针，将第二个链表的尾指针指向第一链表的头指针即可。

Linklist Link(Linklist &h1,Linklist&h2)
{
	Lnode *pa,*pb;//pa,pb用来分别指向两个链表的尾结点 
	pa=h1;
	while(pa->next!=h1)//遍历到循环单链表的最后一个结点 
	{
		pa=pa->next;
	}
	pa->next=h2;//将h1链接在h2前面 
	
	pb=h2;
	while(pb->next!=h2)
	{
		pb=pb->next;
	}
	
	pb->next=h1;
	return h1;
}

13.首先在双链表中查找值为x的结点，查到后取下该节点，然后向前查找第一个大于该结点的位置，并且插入到该位置。

DLinklist Locate(DLinklist &L,int x)
{
	Dnode *p=L->next,*q;//p为工作指针，q为p的前驱，用于查找插入位置 
	//找到频度为x的结点 
	while(p&&p->data!=x) p=p->next;
	if(p==NULL) exit(0);
	else{
		p->freq++;
		//合法就直接返回 
		if(p->pre->freq > p->freq ||p->pre==L) return p;
		//将p摘下来
		if(p->next!=NULL) p->next->pre=p->pre;
		p->pre->next=p->next;
		//向前查找第一个大于该频度的结点
		q=p->pre;
		while(p!=L && q->freq <= q->pre->freq) q=q->pre;
		
		//找到以后插入该结点 
		p->next=q->next;
		if(q->next!=NULL) q->next->pre=p;
		q->next=p;
		p->pre=q;
	}
	
	return p;
}

14.首先遍历计算链表长度n，并将尾结点和首结点相连，得到一个循环单链表。然后找到新链表的尾结点，它是原链表的第n-k个结点，那么n-k+1个结点便是新的表头，最后将第n-k个结点指向null，将环断开。

typedef struct Lnode{
	int data;
	Lnode *next;
}Lnode,*Linklsit;

Linklsit Rightmove(Linklsit L,int k)
{
	Lnode *p=L;
	int n=0;
	while(p->next!=NULL) p=p->next,n++;//找到最后一个位置和计算链表长度
	p->next=L;
	for(int i=0;i<n-k;i++)//此时p还指向最后一个结点 所以是n-k次
	{
		p=p->next;
	}
	
	L=p->next;//改变表头位置
	p->next=NULL;//断环
	
	return L;
}

时间复杂度为$O(n)$,空间复杂度为$O(1)$

15.快慢指针的思想
设置指针fast和指针slow最初都指向头结点。slow走一步，fast走两步，如果链表中存在环，fast会比slow先进入环中，那么若干次以后两个指针一定会相遇。
当slow刚进入环的时候，fast早就已经入环，所以fast与slow的距离小于环的长度，fast每次比slow多走一步，因此当fast和slow相遇时，slow走的距离不会超过环的长度。

由上图的结论，因此可以设两个指针一个指向L，一个指向相遇点，此时两个指针同步移动，最后两者相遇时就是环的入口。

typedef struct Lnode{
	int data;
	Lnode *next;
}Lnode,*Linklsit;

Linklsit Findloop(Linklsit L)
{
	Lnode *fast=L,*slow=L;
	while(fast->next!=NULL and fast->next->next!=NULL)
	{
		fast=fast->next->next;//快指针每次走两步
		slow=slow->next;//慢指针每次走一步
		if(slow==fast) break;//相遇了就退出
	}
		
	if(fast->next==NULL or fast==NULL) return NULL; //没有环返回null
	
	Lnode *p1=L,*p2=slow;//此时p2是相遇点
	while(p1!=p2){
		p1=p1->next;
		p2=p2->next;
	}

	return 	p1;
	
	
}

16.先使用快慢指针的思路找到中间结点(n/2)，然后从中间结点的下一个结点开始头插法建立新的链表，这样便实现了后半段链表的翻转，然后再同时遍历找最大值即可。

typedef struct Lnode {
	int data;
	Lnode *next;
}Lnode,*Linklist ;

int Parisum(Linklist L)
{
	Lnode *slow=L,*fast=L->next;//利用快慢指针找到中间结点
	//注意起始点fast要比slow多一个位置
	while(fast->next!=NULL &&fast!=NULL)
	{
		fast=fast->next->next;
		slow=slow->next;
	}
	
	Lnode *tmp,*p=slow,*news=NULL;
	//tmp为p结点的下一结点，p为工作指针，news为新的表头
	
	while(p->next!=NULL){//头插法来翻转后半段链表
		tmp=p->next;//方便p移动到下一个位置
		p->next=news;//将该结点连接到新的链表的首结点之前
		news=p;//更新首结点位置
		p=tmp;//更新p的位置
	}
	
	p=L;
	Lnode *q=news;//让q遍历新链表
	int mx=0;
	while(q->next!=NULL)
	{
		if(q->data+p->data >mx) mx=q->data+p->data;
		q=q->next;
		p=p->next;
	}
	
	return mx;
	
}

17.设置p、q指针，当p移动了k个位置以后，q指针再开始移动，此时当p指针移动到NULL的时候，q的位置即为倒数第k个结点。

typedef struct Lnode {
	int data;
	Lnode *next;
}Lnode ,*Linklist;

int Searchk(Linklist L,int k)
{
	Lnode *p=L->next,*q=L->next;//当p到达第k个位置时，q再开始移动	
	int cnt=0;//cnt可以用来统计链表长度和作为q开始移动的标志
	while(p!=NULL)//不是p->next!=null  因为要到达倒数第一个结点 p需要为NULL
	{
		if(cnt<k) cnt++;
		else  q=q->next;
		p=p->next;
	}
	
	if(k>cnt) return 0; //k太大 大于表长 不合法
	else {
		printf("%d",q->data);
		return 1;
	}
	
}

时间复杂度为$O(n)$

18.分别求出两个链表的长度，设p、q指针分别指向str1和str2的头结点，从较长的链表开始遍历，找到一个结点其到尾结点的距离等于较短的链表的长度，然后开始同步遍历。

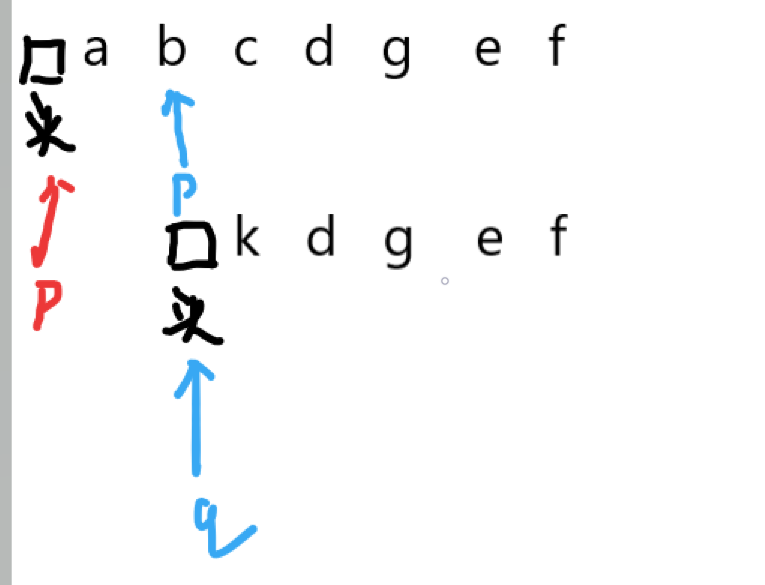
typedef struct Lnode {
	char data;
	Lnode *next;
}Lnode ,*Linklist;

int getlen(Linklist L)
{
	Lnode *p=L;
	int len=0;
	while(p->next!=NULL){
		len++;
		p=p->next;
	}
	return len;
}



Lnode  Searchcommon(Linklist str1,Linklist str2)
{
	Lnode *p=str1,*q=str2;
	int len1=getlen(str1);
	int len2=getlen(str2);
	
	for(int i=0;i<len1-len2;i++) //谁长就先遍历到短的位置的起点
	p=p->next;
	for(int i=0;i<len2-len1;i++)
	q=q->next;
	
	//找到开始位置后，同时向后移动
	while(p!=q)
	{
		p=p->next;
		q=q->next;
	}
	
	return p;
	
}

19.使用空间换时间，申请内存作为标记数组，遍历链表若当前结点的下一结点没有标记过则标记并保留，若标记过则删除该节点。

typedef struct Lnode {
	char data;
	Lnode *next;
}Lnode ,*Linklist;


void  Deletesame(Linklist &L,int n)
{
	Lnode *p=L,*r;
	int *q;
	q=(int *)malloc(sizeof(int)*(n+1));//用来标记是否出现过
	for(int i=0;i<n+1;i++) *(q+i)=0;//初始化为0
	
	int m;
	while(p->next!=NULL)
	{
		m= p->next->data>0? p->next->data:-p->next->data;//绝对值
		if(*(q+m)==0) {//没标记过的标记一下
			*(q+m)=1;
			p=p->next;
		}else{
			r=p->next;
			p->next=r->next;
			free(r);//标记过的释放掉
		}
		
		
	}
	free(q);//用完就释放掉

}

时间复杂度为$O(m)$,空间复杂度为$O(n)$

栈、队列和数组

栈是只允许在一端进行插入或删除操作的线性表。其操作特性可以明显概括为后进先出（LIFO）
栈的数学性质：当n个不同元素进栈时，出栈元素不同排列个数为$\frac{1}{n+1}$$C_{2n}^{n}$

栈

采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针(top)指示当前栈顶元素的位置。
栈的顺序存储类型可描述为

#define MaxSize 50
typedef struct {
	int data[MaxSize];
	int top;
}Sqstack;

顺序栈的基本操作

//栈的初始化
void InitStack(Sqstack &S)
{
	S.top=-1;
}

//判栈空
bool Stackempty(Sqstack S)
{
	if(S.top==-1) return true;
	else return false ;
}

//进栈
bool Push(Sqstack &S,int x)
{
	if(S.top==MaxSize-1) return false;//栈满，报错
	S.data[++S.top]=x;//指针先加1，在入栈，如果为top==0，应该是S.top++
	return true;
}

//出栈
bool Pop(Sqstack &S,int &x)
{
	if(S.top==-1) return false;
	x=S.data[S.top--];
	return true;
}

//读栈顶元素
bool Gettop(Sqstack S,int &x)
{
	if(S.top==-1) return false;
	x=S.data[S.top];
	return true;
}

共享栈
利用栈底位置相对不变的特性，可以让两个顺序栈共享一个一维数组空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸，如图所示：

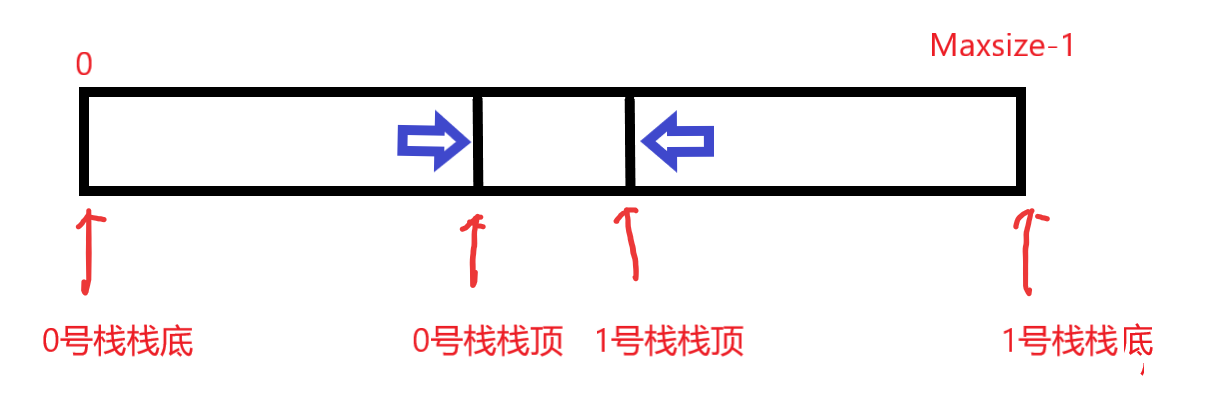
两个栈的栈顶元素都指向栈顶元素
top0==-1时0号栈为空，top1=Maxsize时一号栈为空
栈满的条件为top1-top0==1
当0号栈进栈时top0先加一再赋值，1号栈进栈时top1先减一再赋值；出栈则刚好相反

栈的链式存储结构
采用链式存储的结构的栈称为链栈，其优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。
规定链栈没有头结点

typedef struct Linknode{
	int data;
	struct Linknode *next;
}LitStack;

练习题

易错题

$1.栈和队列具有相同的()$

\[A.抽象数据类型\quad B.逻辑结构\quad C.存储结构\quad D.运算 \]

$2.设链表不带头结点且所有操作均在表头进行，则下列最不合适作为链栈的是()$
$A.只有表头结点指针，没有表尾指针的双循环链表$
$B.只有表尾结点指针，没有表头指针的双循环链表$
$C.只有表头结点指针，没有表尾指针的单循环链表$
$D.只有表尾结点指针，没有表头指针的单循环链表$

$3.向一个栈顶指针为top的链栈(不带头结点)中插入一个x结点，则执行()$
$A.top->next=x$
$B.x->next=top->next;\quad top->next=x$
$C.x->next=top;\quad top=x$
$D.x->next=top;\quad top=top->next$

$4.设a,b,c,d,e,f以所给的次序进栈，若在进栈操作时，允许出栈操作，则下面得不到的出栈序列为$

\[A.fedcba\quad B.bcafed\quad C.dcefba\quad D.cabdef \]

$5.若栈的输入顺序是P_1,P_2,...,P_n，输出序列是1,2,3,...,n,若P_3=1,则P_1的值（）$

\[A.可能是\quad B.一定是2\quad C.不可能是2\quad D.不可能是3 \]

$6.【2011统考真题】元素a,b,c,d,e依次进入初始为空的栈中，若元素进栈后可停留、可出栈，直到$
$所有元素都出栈，则在所有可能的出栈序列中，以元素d开头的序列个数是()$

\[A.3\quad B.4\quad C.5\quad D.6 \]

$7.【2013统考真题】一个栈的入栈序列为1,2,3,...,n，出栈序列是P_1,P_2,...,P_n$
$若P_2=3，则P_3的可能取值的个数为()$

\[A.n-3\quad B.n-2\quad C.n-1\quad D.无法确定 \]

答案

C
解释：两者的存储结构都有顺序存储和链式存储
C
解释：链栈所有的操作都是在表头进行的，所以要让我们迅速的找到头结点，循环双链表肯定是O（1），带尾指针的单向循环链表也可以O（1）的找到头结点，但是只有头指针每次都要遍历整个链表一次，复杂度为O（n）。
C
解释：链栈的操作都是在表头进行的，所以x->next=top,top=x。直接将结点指向表头，然后更新栈顶指针。
D
解释：对于某个出栈的元素，在它之前进栈却比它晚出栈的元素必定按逆序出栈，ab在c之前进栈，所以c出栈以后，ab应该是按照ba出栈的才对。
C
解释：p3是1，p1，p2比p3先进入序列，但是比p3后出序列，所以输出必是p3，p2，p1；输出序列为123，根据上一题标黑的解释，所以必不可能p1为2。

综合应用题

$1.栈的初态和终态始终为空，以I和O分别表示入栈和出栈，则出入栈的操作序列可表示为由I和O组成的$
$序列，可以操作的序列称为合法序列，否则称为非法序列。$

$1).写出一个算法，判定所给的操作序列是否合法。若合法，返回true，否则返回false(假定被判定的操$
$作序列已存入一维数组中)$

$2.设单链表的表头指针为L，结点结构由data和next两个域构成，其中data域为字符型。试设计算法判断$
$该链表的全部n个字符是否中心对称。例如xyx、xyyx都是中心对称$

$3.设有两个栈S1、S2都采用顺序栈方式，并共享一个存储区[0,...,maxsize-1],为了尽量利用空间，减$
$少溢出的可能，可采用栈顶相向、迎面增长的存储方式。试设计S1、S2有关入栈和出栈的操作算法。$

答案
1.模拟栈验证的思想，直接遍历已经存了IO的字符串数组，统计入栈和出栈的次数，最后看是否相等即可。

int  check (char A[])
{
    //当前的IO 已经存在字符数组里面了
    //j用来统计I的个数，k用来统计O的个数
    int i=0;
    int j,k;
    j=k=0;
    while(A[i]!='\0')
    {
        if(A[i]=='I'){
            j++;
        }else if(A[i]=='O')
        {
            k++;
        }
        i++;
    }
    if(j!=k){
        cout<<"序列非法";
        return 0;
    }else{
        cout<<"合法序列";
        return 1;
    }
    
}

2.把链表前半段元素存在数组里，然后模拟栈的验证，从尾往前开始扫数组，并从后半段的第一个元素开始指针往后移，检查对应元素是否相等即可。

typedef struct Lnode {
    char data;
    Lnode *next;
}Lnode,*Linklist;


int  check(Linklist L,int n)
{
    //把链表前一半的元素存在数组里
    //然后从后往前遍历数组 从中间继续往后遍历链表 验证两者是否相等
    char s[n/2];
     Lnode *p=L->next;
     int i;
    for( i=0;i<n/2;i++)
    {
        s[i]=p->data;
        p=p->next;
    }
    i--;//记得退一位
    
    //循环完p指到后半段的第一个节点
    //如果是奇数还要再往后移一个节点
    if(n&1) p=p->next;
    while(p!=NULL && s[i]==p->data){
        i--;
        p=p->next;
    }
    if(i==-1) return 1;
    else return 0;
}

3.共享栈的原理实现一下即可

typedef struct {
    int data[maxsize];
    int top[2];
}stk;

stk s;

int push(int i,int x) //i为栈号，x为元素
{
    if(i<0||i>1) {
        cout<<"栈号输入不对"<<endl;
        exit(0);
    }
    if(s.top[1]-s.top[0]==1) {//共享栈 栈满的条件
        cout<<"栈已经满了"<<endl;
        return 0;
    }
    
    if(i==0) {
        s.data[++s.top[0]]=x;
        return 1;
    }
    if(i==1)
    {
        s.data[--s.top[1]]=x;
        return 1;
    }
}

int pop(int i)
{
    //退栈成功返回退栈元素，否则返回-1
     if(i<0||i>1) {
        cout<<"栈号输入不对"<<endl;
        exit(0);
    }
    if(i==0)
    {
        if(s.top[0]==-1) {
            cout<<"栈空"<<endl;
            return -1;
        }
        else {
        return     s.data[s.top[0]--];
        }
    }
    
    if(i==1)
    {
        if(s.top[1]==maxsize)//注意这里是maxsize
        {
            cout<<"栈空"<<endl;
            return -1;
        }else{
            return s.data[s.top[1]++];
        }
        
    }
}

队列

队列操作的特性是：先进先出。

队列的顺序存储

初始时：Q.front =Q.rear =0。
进队操作：队不满时，先送值到队尾元素，再将队尾指针加一。
出队操作：队不空时，先取队头元素值，再将队头指针+1。

#define maxsize 50
typedef struct{
    int data[maxsize];
    int front,rear;
}Sqqueue;

由于顺序队列无法很好的判断队满时的情况，所以我们一般使用循环队列。

循环队列

循环队列：将顺序队列臆造为一个环状的空间，即把存储队列元素的表从逻辑上视为一个环。
当队首指针Q.front=maxsize-1后，再前进一个位置就自动到0，这可以利用除法取余（%）来实现

初始时：Q.front = Q.rear =0
队首指针进1：Q.front=(Q.front+1)%maxsize
队尾指针进1：Q.rear=(Q.rear+1)%maxsize
队列长度：(Q.rear+maxsize-Q.front)%maxsize
出队入队时：指针都要按顺时针方向+1

循环队列队空/队满的三种处理方式

牺牲一个单元来区分队满还是队空，入队时少用一个队列单元，这是一种比较普遍的做法，约定以“队头指针在队尾指针的下一个位置作为队满的标志”

队满条件：(Q.rear+1)%maxsize==Q.front。
队空条件：Q.front==Q.rear
队列中元素的个数：(Q.rear-Q.front+maxsize)%maxsize

类型中增设size数据成员，表示元素个数。删除成功则size-1，插入成功则size+1。队列空时Q.size==0;队满时Q.size=maxsize,两种情况都有Q.front=Q.rear。

3.类型中增设tag数据成员，以区分队满还是队空。删除成功置tag=0，若导致Q.front=Q.rear,则为队空；插入成功则置tag=1，若导致Q.front==Q.rear,则为队满。

循环队列的操作

//初始化
void InitQueue(sqqueue &Q)
{
    Q.front=Q.rear=0;
}

//判队空
bool isempty(sqqueue Q)
{
    if(Q.rear==Q.front) return true;
    else return false;
}

//入队
bool Enqueue(sqqueue &Q,int x)
{
    if((Q.rear+1)%maxsize==Q.front) return false;//队满则报错
    Q.data[Q.rear]=x;
    Q.rear=(Q.rear+1)%maxsize;//队尾指针+1取模
    return true;
}

bool Dequeue(sqqueue &Q,int &x)
{
    if(Q.rear==Q.front) return false;
    x=Q.data[front];
    Q.front=(Q.front+1)%maxsize;
    return true;
}

队列的链式存储

1.队列的链式存储
队列的链式表示称为链队列，它实际上是一个同时拥有队头指针和队尾指针的单链表。

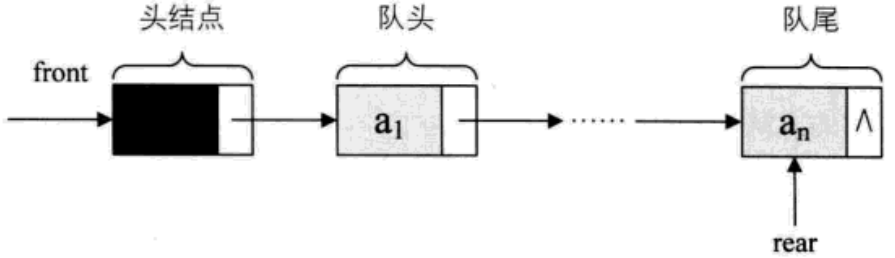
队列的链式存储可以描述为

typedef struct Linknode{
	int data;
	struct Linknode *next;
}Linknode;

typedef struct {
	Linknode *front,*rear;
}Linkqueue;

不带头结点时，当$Q.front=NULL$且$Q.rear=NULL$时，链式队列为空。

入队时，建立一个新结点插入到链表的尾部，并让$Q.rear$指向这个新插入的结点（若原队列为空队，则令$Q.front$也指向该结点）。出队时，首先判断队列是否为空，若不空，则取出队头元素，将其从链表摘除，并让$Q.front$指向下一个结点（若该结点为最后一个结点，则置$Q.front$和$Q.rear$都为$NULL$）。
不难看出，不带头结点的链式队列在操作上往往比较麻烦，因此通常将链式队列设计成一个带头结点的单链表，这样插入和删除就统一了。

#include <bits/stdc++.h>
using namespace std;

typedef struct Linknode{
	int data;
	struct Linknode *next;
}Linknode ;

typedef struct {
	Linknode *front,*rear;
}Linkqueue;

//初始化
void Initqueue(Linkqueue &Q)
{
	Q.front=Q.rear=(Linknode *)malloc (sizeof (Linknode));//建立头结点
	Q.front->next=NULL;//初始为空
}

//判队空
bool Isempty(Linkqueue &Q)
{
	if(Q.front==Q.rear) return true;
	else return true;
	
}

//入队
void Enqueue(Linkqueue &Q,int x)
{
	Linknode *s=(Linknode *)malloc(sizeof (Linknode));//创建新结点
	s->data=x;
	s->next=NULL;
	Q.rear->next=s;//插入链尾
	Q.rear=s;//插入尾指针,Q.rear指向新的结点
}


//出队
bool Dequeue(Linkqueue &Q,int &x)
{
	//Q.front是指向头结点的
	if(Q.front==Q.rear) return false; //空队列
	Linknode *p=Q.front->next;
	x=p->data;
	Q.front->next=p->next;
	if(Q.rear==p) Q.rear=Q.front;//若原队列只有一个结点，删除后变空
	free(p);
	return true;
}

双端队列

双端队列是指允许两端都可以进行插入删除操作的线性表。
我们通常将左端视为前端，右端也视为后端。

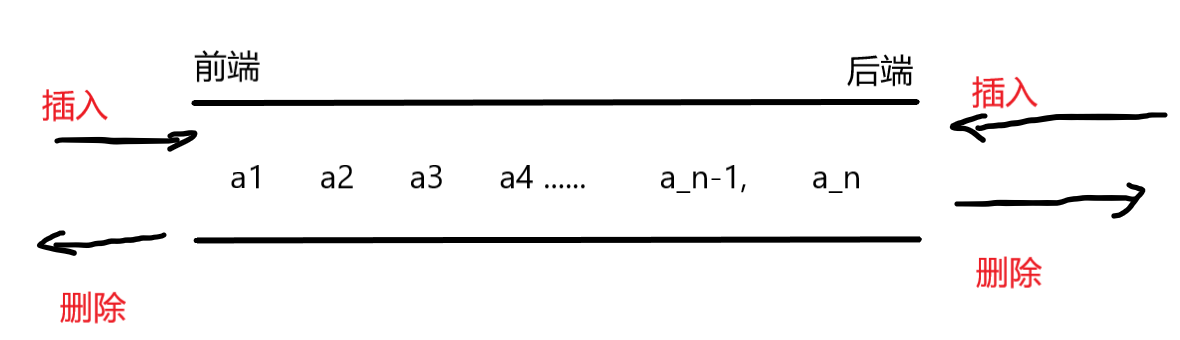
考题通常会出某一端输出受限或输入受限的双端队列，考察其按某个顺序输入，其输出序列是神马。
输出受限的双端队列：允许在一端进行插入删除，但在另外一端只允许插入的双端队列称为输出受限的双端队列。
输入受限的双端队列：允许在一端进行插入删除，但在另外一端只允许删除的双端队列称为输入受限的双端队列。

练习题

$1.已知循环队列的存储空间为数组A[21],front指向队头元素的前一个位置，rear指向队尾元素，假设当前的$
$front和rear的值分别为8和3，则该队列的长度为()$

\[A.5\quad B.6\quad C.16\quad D.17\quad \]

$2.假设用A[0...n]实现循环队列，front、rear分别指向队首元素的前一个位置和队尾元素。若用(rear+1)%(n+1)==front$
$作为队满标志，则()$
$A.可用rear==front作为队空标志$
$B.队列中最多n+1个元素$
$C.可用front>rear作为空标志$
$D.可用(front+1 ) 取余（n+1）== rear作为队空标志 $

$3.与顺序队列相比，链式队列()$
$A.优点是队列的长度不受限制$
$B.优点是进队和出队的时间效率更高$
$C.缺点是不能进行顺序访问$
$D.缺点是不能根据队首指针和队尾指针计算队列的长度$

$4.【2011统考真题】已知循环队列存储在一维数组A[0...n-1]中，且队列非空时front和rear分别指向队头和队尾元素。若初始$
$队列为空，且要求第一个进入队列的元素存储在A[0]处，则初始时front和rear的值分别是()$

\[A.0,0\quad B.0,n-1\quad C.n-1,0\quad D.n-1,n-1\quad \]

答案

C
解释：Q.(rear-front+Maxsize)%Maxsize 就是队列元素的个数
A
解释：牺牲一个存储单元来区分队空和队满，所以可以用front==rear来表示队空，也可以自己手动模拟。
D
解释：顺序队列可以通过队头指针和队尾指针来计算元素个数，但是链式队列不行。
B
解释：入队时rear+1，front不变，所以应该让front=0，rear=n-1

算法应用题
$1.若希望循环队列中的元素都可以得到利用，则需要设置一个标志域tag，并以tag为0或1来区分队头指针front和队尾指针rear$
$相同时队列的状态时"空"还是“满”。试编写与此结构相应的入队和出队算法$

答案
1.tag为1表示入队，tag为0表示出队

#define maxsize 50
typedef struct {
	int data[maxsize ];
	int front, rear;
	int tag;
} SqQueue;

int EnQueue(SqQueue &Q, int x) {
	if (Q.tag == 1 && Q.front == Q.rear) return 0;//两个条件都满足时则队满
	Q.tag = 1;
	Q.data[Q.rear] = x;
	Q.rear = (Q.rear + 1) % maxsize;
	return 1;
}

int DeQueue(SqQueue &Q, int &x) {
	if (Q.tag == 0 && Q.rear == Q.front) return 0;//两个条件都满足则队空
	Q.tag = 0;
	x = Q.data[Q.front];
	Q.front = (Q.front + 1) % maxsize;
	return 1;
}

树与二叉树

树的基础概念

树的定义：
树是$n$个结点的有限集，当$n=0$时，称为空树。任意一颗非空树应该满足

有且仅有一个特定的称为根的结点
当$n>1$时，其余结点可以分为$m(m>0)$个互不相交的有限集，其中每个有限集本身又是一棵树，并且称为根的子树。

显然，树的定义是递归的，即在树的定义中又用到了其自身，树是一种递归的数据结构。树作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点：

树的根节点没有前驱，除根节点外的所有结点有且只有一个前驱。
树中的所有结点都可以有零个或者多个后继

一些基本的术语不再赘述，看书复习。

树的性质

树的结点数n等于所有结点的度数之和加1。
度为m的树中第i层上至多有$m^{i-1}$个结点(i>=1)
高度为$h$的$m$叉树至多有（$m^h-1$）/($m-1$)个结点
度（树中结点最大度数）为$m$，具有$n$个结点的树的最小高度$h$为$log_m(n(m-1)+1)$向上取整
度为$m$，具有n个结点的树的最大高度$h$为$n-m+1$。

二叉树的概念

二叉树的定义
二叉树是一种特殊的树形结构，其特点是每个结点最多只有两颗子树(即二叉树中不存在度大于2的结点)，并且二叉树的子树有左右之分，其次序不能任意颠倒。

与树相似，二叉树也以递归的形式定义。

二叉树是有序树，若将其左右子树颠倒，则成为另一颗不同的二叉树，即使树中结点只有一颗子树，也要区分它是左子树还是右子树。

二叉树与度为2的有序树的区别

度为2的树至少要有3个结点，而二叉树可以为空。
度为2的有序树的孩子的左右次序是相对于另一个孩子而言的，若某个结点只有一个孩子则无需区分其左右次序，而二叉树无论其孩子数是否为2，均需确定其左右次序，即二叉树的结点次序不是相对于另一结点而言的，而是确定的。

几种特殊的二叉树

满二叉树。一棵树的高度为$h$，且有$2^h-1$个结点的二叉树称为满二叉树，即二叉树中每层都含有最多的结点。
可以对二叉树按层序编号：约定编号从根结点(根结点编号为1)起，自上而下，自左而右。这样，每个结点对应一个编号，对于编号为$i$的结点，若有双亲，则其为$i/2$，若有左孩子，则左孩子为$2i$；若有右孩子，则右孩子为$2i+1$

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
//二叉树的链式存储
typedef struct bitree{
	int data;
	struct bitree *lc,*rc;
}*Bitree,Bitnode;

Bitnode *p;//p指向目标结点
Bitnode *pre=NULL;//指向当前访问结点的前驱
Bitnode *final=NULL;//用于记录最终结果

//二叉树找中序前驱
//原理是：pre遍历的是q的上一个结点，如果p==q那么此时的pre就是p的前驱

void visit(Bitnode *q)
{
	if(p==q) final =pre; //当前
	else pre=q;
}



void Inorder(Bitree T)
{
	if(T!=NULL) {
		Inorder(T->lc);//递归遍历左子树
		visit(T);//访问根节点
		Inorder(T->rc);
	}
}

中序线索二叉树的构造

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
//线索二叉树结点
typedef struct Threadnode{
	int data;
	struct Threadnode *lc,*rc;
	int ltag,rtag;
}Threadnode,*Threadtree;


void Inthread(Threadtree &p, Threadtree &pre)
{
	if(p!=NULL)
	{
		Inthread(p->lc,pre);//递归，线索化左子树
		
		//---------处理根------------------------------
		if(p->lc==NULL){//当前结点的左子树为空
			p->lc=pre;//建立当前结点的后继线索
			p->ltag=1;
		}
		if(pre!=NULL&&pre->rc==NULL)//前驱结点非空且其右子树为空
		{
			pre->rc=p;//建立前驱结点的后继线索
			pre->rtag=1;
		}
		pre=p;//标记当前结点为刚刚访问过的结点
		
		//---------------------------------------------------
		Inthread(p->rc,pre);//递归线索化右子树
	}
	
	
}


void CreatinThread(Threadtree T)
{
	Threadnode *pre=NULL;
	if(T!=NULL){
		Inthread(T,pre);
		pre->rc=NULL;
		pre->rtag=1;
	}
	
}

posted on 2024-09-29 10:58 swj2529411658 阅读(3) 评论(0) 编辑收藏举报

刷新页面返回顶部

swjswjswj

数据结构

顺序表

线性表的顺序表示

顺序表的定义

易错题

顺序表上基本操作的实现

练习题

答案

线性表的链式表示

单链表的定义

单链表上基础操作的实现

单链表的插入删除

单链表的查找

单链表的建立

双链表

循环链表

静态链表

顺序表和链表的比较

练习题

易错题

综合应用题

栈、队列和数组

栈

练习题

易错题

综合应用题

队列

队列的顺序存储

循环队列

队列的链式存储

双端队列

练习题

树与二叉树

树的基础概念

二叉树的概念

导航

公告