数据结构实验第一周

6-1 差距几何

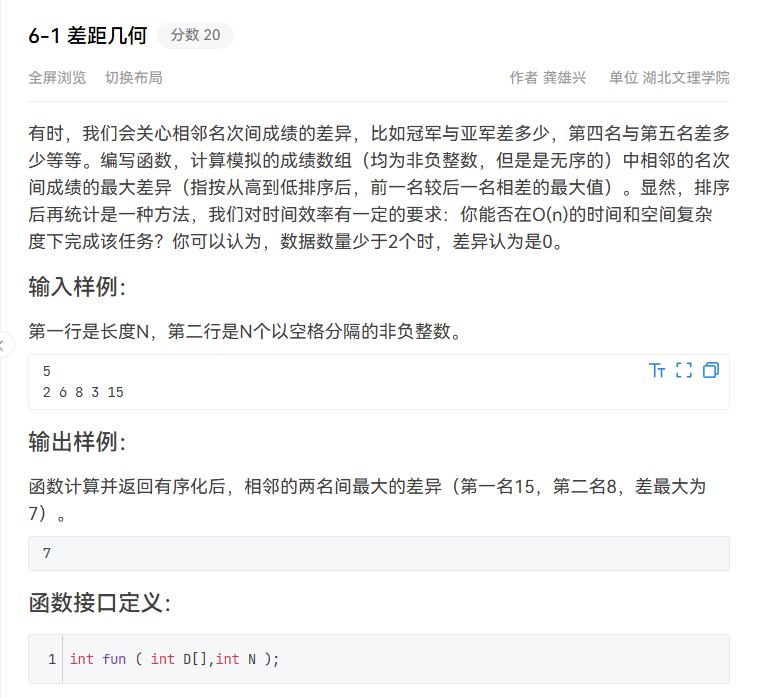
排序的话复杂度要O(n),可以选择桶排序或者计数排序，我选择的是计数排序
比如是 3 2 1 4 4 7 8 6
我开一个数组a [9] (因为最大为8)，然后分别对出现的数计数有
a：1 1 1 2 0 1 1 1 0
然后按顺序放回 就是1 2 3 4 4 6 7 8

int fun(int D[],int N)
{
    if(N<2) return 0;
    int mx=0;//用来看最多要开多大的数组
    for(int i=0;i<N;i++)
        if(mx<D[i]) mx=D[i];
    
    int len=mx+1;
    int tp[len];
    for(int i=0;i<len;i++) tp[i]=0;//先对计数数组初始化
    for(int i=0;i<N;i++) tp[D[i]]++;//计数

    //放回的过程
    for(int i=0,j=0;i<len;i++)
    {
        while(tp[i]!=0)
        {
            D[j]=i;
            j++;
            tp[i]--;
        }
    }
    int ans=-1;
    for(int i=1;i<N;i++)
    if(D[i]-D[i-1]>ans) ans=D[i]-D[i-1];//找相邻最大值
    return ans;
}

6-2 最大子段和* - 《C++编程基础及应用》- 习题7-4

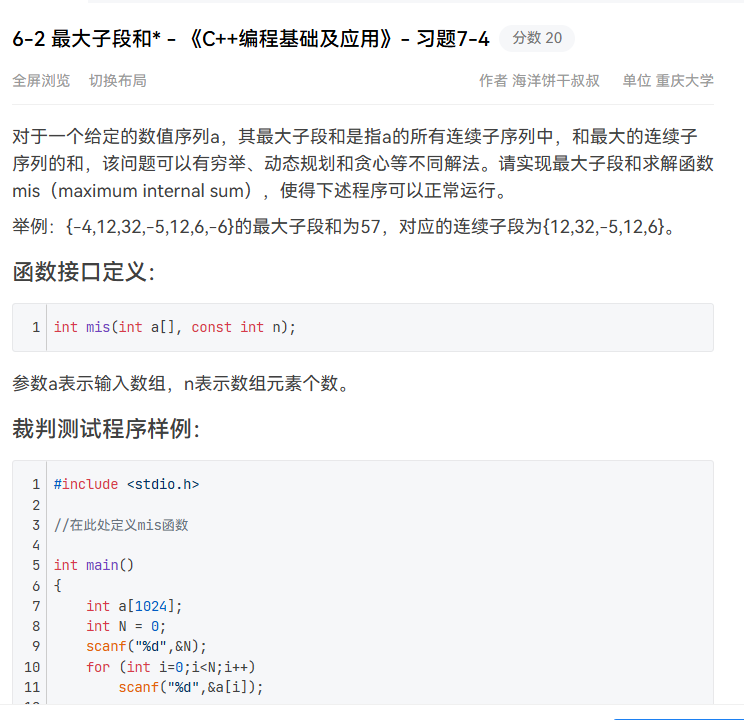
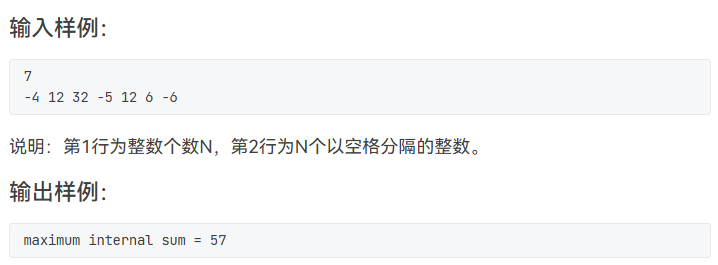
这道题可以选择两层循环的暴力做法，或者使用dp的做法，建议学习一下dp的做法
dp的做法跟第三题是一样的
这里写的暴力做法，dp看最后一题

int mis(int a[],const int n)
{
    //两层循环可以遍历到所有的连续线段
    //找到最大值即可
        int ans=0;
      for(int i=0;i<n;i++)
      {
          int tmp=0;
          for(int j=i;j<n;j++)
          {
              tmp+=a[j];
              if(tmp>ans) ans=tmp;
          }
      }
    return ans;
}

7-1 最大子列和问题


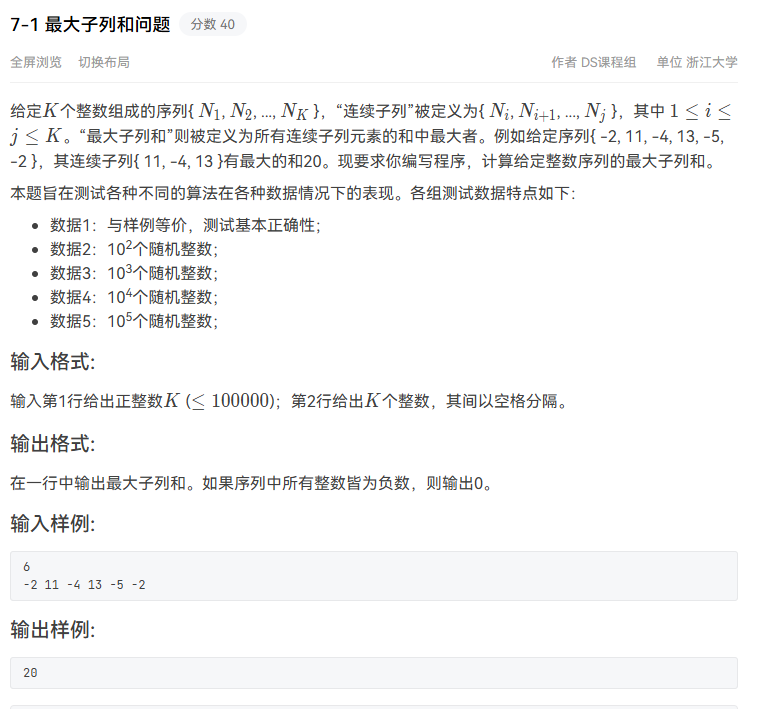
dp的状态转移方程为

\[dp[i]= \begin{cases} dp[i-1]+a[i]& \text{, dp[i-1]>0}\\ a[i]& \text{dp[i-1]<=0} \end{cases}\]

举样例给大家体会一下
a[i]：-2 11 -4 13 -5 -2
dp[i]: -2 11 7 20 15 13
所以答案是20

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int n;
    cin>>n;
    int a[100005];
    for(int i=0;i<n;i++) cin>>a[i];
    int dp[100005];
    dp[0]=a[0];//记得初始化
    int ans=0;
    for(int i=1;i<n;i++)//从1开始
    {
        if(dp[i-1]>0) dp[i]=dp[i-1]+a[i];
        else dp[i]=a[i];
        ans=max(ans,dp[i]);//维护最大值
    }
    cout<<ans;
}