拓扑排序+反向拓扑

拓扑排序：是一个有向无环图的所有顶点的线性序列。且该序列必须满足两个条件

1. 每个顶点出现且只出现一次。
2. 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

Kahn（卡恩）算法
算法的核心用队列维护一个入度为0的节点的集合。

1. 初始化，队列q压入所有入度为0的点；
2. 每次从q中取出一个点x放入数组tp；
3. 然后将x点所有出边删除，若将边（x,y）删除以后，y的入度变为0，则将y压入q中。
4. 不断重复2，3过程，直到队列为空。
5. 若tp中的元素个数等于n则有拓扑序，否则有环。

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=50005;
int n,m;
vector<int>e[N],tp;//tp存拓扑序列，e存点x的邻点
int din[N];//存点x的入度

//用队列维护一个入度为0的节点的集合
bool toposort(){
    queue<int>q;
    //放入度为0的点
    for(int i=1;i<=n;i++)
    {
        if(din[i]==0) q.push(i);
    }
    
    while(q.size()){
        int x=q.front();q.pop();
        tp.push_back(x);
        for(auto t:e[x])
        {
            if(--din[t]==0) {
                q.push(t);
            }
            
        }
    }
    return tp.size()==n;

}


signed main()
{
   cin>>n>>m;
   for(int i=0;i<m;i++)
   {
       int u,v;
       cin>>u>>v;
       e[u].push_back(v);
       din[v]++;
   }
    if(!toposort()) cout<<-1;
    else for(auto t:tp) cout<<t<<" ";

}

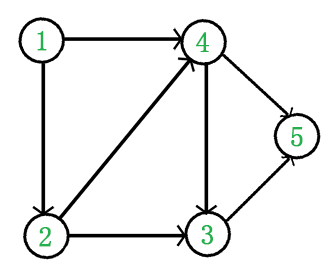
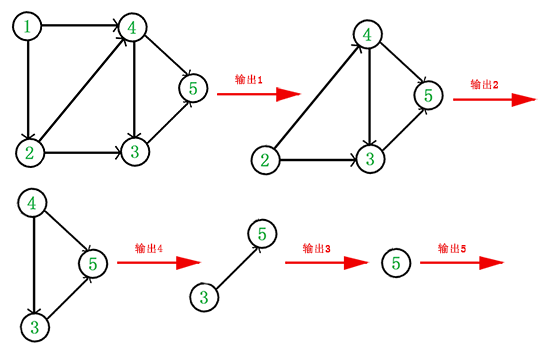
反向拓扑：在一个图的拓扑排序问题中，因为常常不止有一种排序方式，所以题目往往要求在所有排序方式中，让序号小的尽量排前（只要满足拓扑条件），此时要使用优先队列大根堆来维护。
并且，此时我们是把出度为0的点放入队列，所以需要反向建边。
参考 https://www.cnblogs.com/atmacmer/p/5178666.html
理解了这个只需要修改自己的拓扑排序模版即可。
模版题P3243 [HNOI2015] 菜肴制作

#include <bits/stdc++.h>
#define int long long
using namespace std;
int d,n,m,p;
int din[100005];//反向拓扑时，此时这里应该叫做出度
//---------链式前向星存图------
struct Edge{
    int to;
    int next;
}e[100005];

int tp[100005];//存放拓扑序列
int head[100005],idx;
void add(int u,int v)
{
    e[idx].to=v;
    e[idx].next=head[u];
    head[u]=idx++;
}

//----------------------------


//反向拓扑的模版-----------------------------
bool toposort()
{
    priority_queue<int>q;//大根堆
    for(int i=1;i<=n;i++)
    {
        if(!din[i]) q.push(i);//出度为0的点放入
    }
    
    while(q.size())
    {
        auto t=q.top(); q.pop();
        tp[++p]=t;
        for(int i=head[t];i!=-1;i=e[i].next)
        {
            if(--din[e[i].to]==0) q.push(e[i].to);
        }
        
    }
    
    if(p==n) return 1;
    return 0;
    
}

void solve()
{
    cin>>n>>m;
    idx=0,p=0;
    memset(head,-1,sizeof head);
    memset(tp,0,sizeof tp);
    memset(din,0,sizeof din);
    for(int i=0;i<m;i++)
    {
        int u,v;
        cin>>u>>v;
        add(v,u);//反向建边，反向拓扑
        din[u]++;//这里注意时din[u]++；
    }
    if(toposort()){
        for(int i=n;i>0;i--) cout<<tp[i]<<" ";//要反向输出
    }else cout<<"Impossible!";
    cout<<endl;
    
}

//----------------------------------------------------------------


signed main()
{
    cin>>d;
    while(d--) solve();
    
}