二叉树知识点

1. 树的介绍

1. 1树的定义

树是一种数据结构，它是由n\((n>=1)\)个有限节点组成一个具有层次关系的集合。

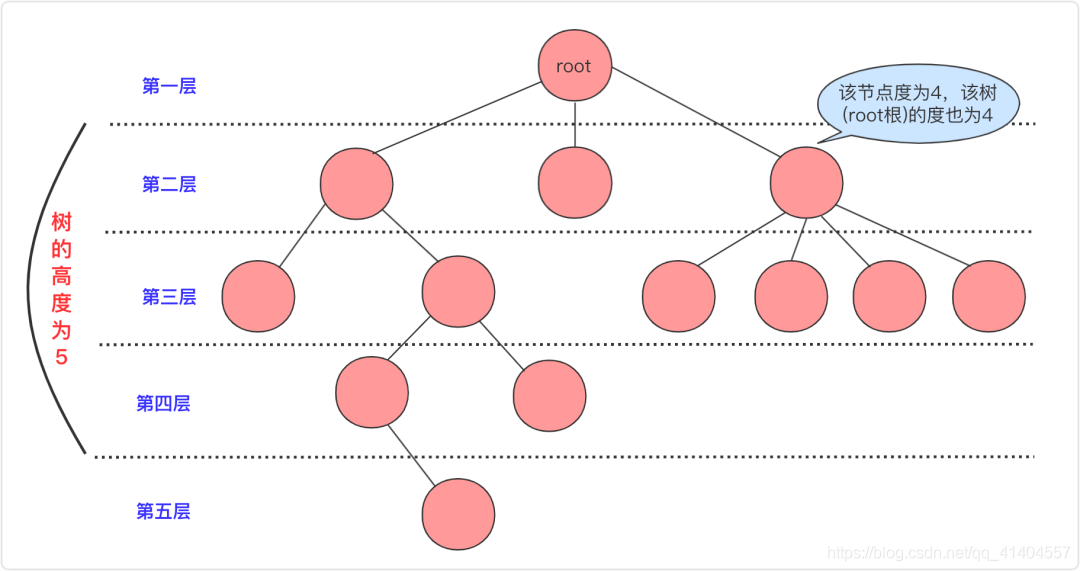
把它叫做树是因为它像一颗倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下特点：

1. 每个节点有零个或多个子节点；
2. 没有父节点的节点称为根节点；
3. 每一个非根节点有且仅有一个父节点；
4. 除了根节点以外，每个子节点可以分为多个不相交的子树。

1.2树的基本术语

若一个节点有子树，那么该节点称为子树根节点的“双亲”，子树的根是该节点的“孩子”。有相同双亲的节点互为“兄弟节点”。一个节点的所有子树上的任何节点都是该节点的后裔。从根节点到某个节点的路径上的所有节点都是该节点的祖先。

• 节点的度：节点拥有子树的数目。
• 叶子：：度为0的节点
• 分支节点：度不为0度节点
• 树的度：树中节点最大的度
• 层次：根节点的层次为1，其余节点的层次等于该节点的双亲节点+1
• 树的高度：树中节点的最大层次
• 无序数：如果树中节点的各子树之间的次序是不重要的，可以交换位置
• 有序数：如果树中节点的各子树的次序是重要的，不可以交换位置。
• 森林：0个或多个不相交的树组成。对森林加上一个根，森林即称为树；删除根，树即成为森林。

1.3相关性质

2.二叉树的介绍

2.1二叉树的定义

二叉树是每个节点最多有两个子树的树结构。它有五种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左右子树皆为空

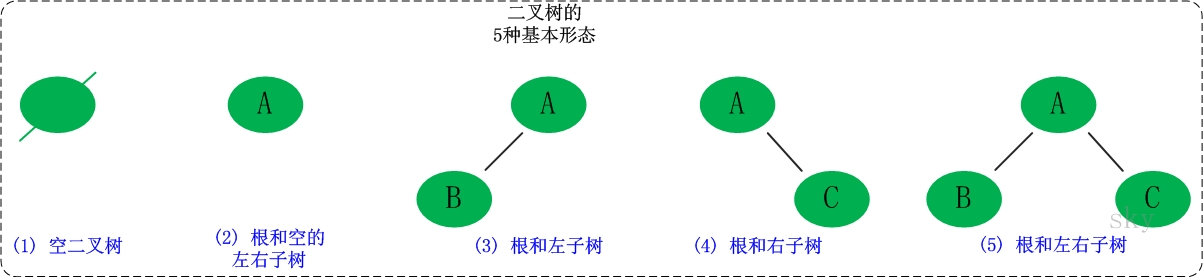
2.2二叉树与度为2的树的区别

1. 度为2的树必须有三个节点以上（否则就不叫度为2了），二叉树可以为空。
2. 二叉树的度不一定为2，比如斜树。
3. 二叉树有左右节点区分，而度为2度树没有左右节点的区分。

2.3二叉树的性质

1. 二叉树第i层上的节点数目最多为2^i-1
2. 深度为k的二叉树至多有2^k-1个节点
3. 包含n个节点的二叉树的高度至少为\(log_2(n+1)\)
4. 在任意一颗二叉树中，若终端节点的个数为\(n_0\)，度为2的节点为\(n_2\)，则\(n0=n2+1\)

3.二叉树的种类

3.1满二叉树

3.1.1定义：

高度为h，并且有2^h-1个节点的二叉树，被称为满二叉树。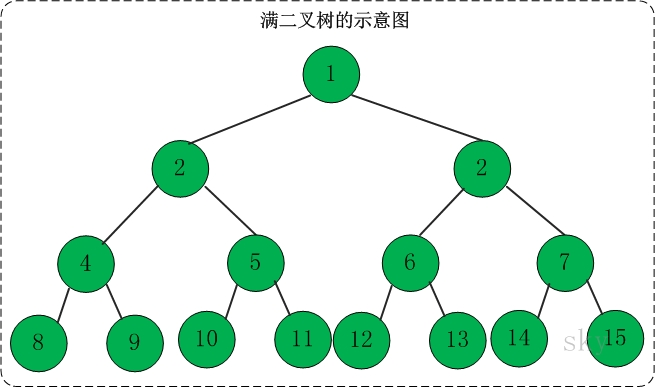

完全二叉树

3.2.1定义：

一颗二叉树，只有最下面两层节点的度可以小于2，并且最下层的叶节点集中在靠左的若干位置上

3.2.2特点：

叶子节点只能出现在最下层和次下层，且最下层的叶子节点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树又不一定是满二叉树。

3.3二叉查找树

3.3.1定义

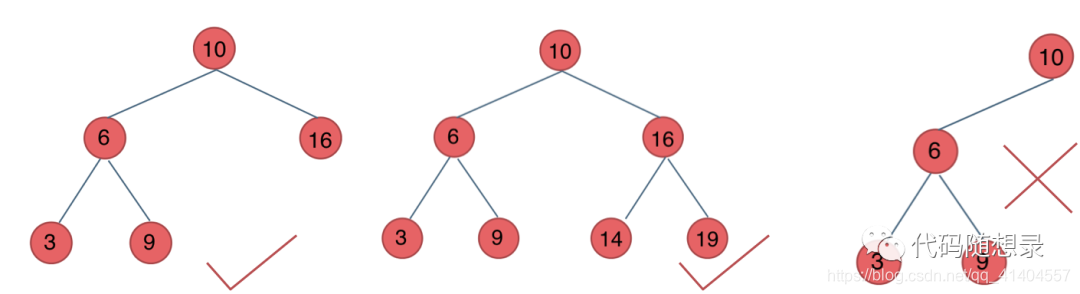
二叉查找树（Binary Search Tree）,又称二叉搜索树。设x为二叉树中的一个节点，x节点包含关键字Key，节点的key值记为Key[x]。如果y是x的左子树中的一个节点，则Key[y]<=Key[x];如果y是x的有子树的一个节点，则Key[y]>=Key[x]。

3.3.2特点

1. 若任意节点的左子树不空，则左子树上所有的值均小于根节点的值。
2. 若任意节点的右子树不空，则右子树上所有节点的值均大于根节点的值（更大于左子树上的值）
3. 任意节点的左右子树叶分别为二叉查找树。
4. 没有键值相等的点。

3.4平衡二叉搜索树

3.4.1定义

平衡二叉搜索树：又称AVL树，具有以下性质：它是一棵空树或者它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

4.二叉树的存储方式

4.1链式存储

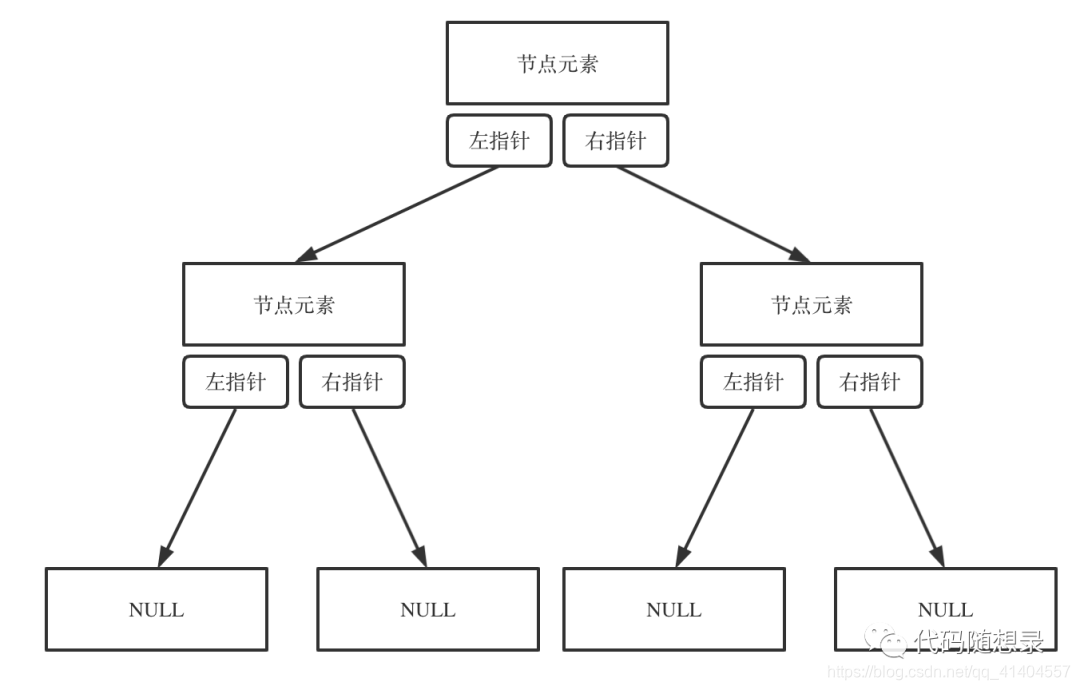
通过指针把分布在散落在各个地址的节点串联在一起，链式存储如图所示：

4.2顺序存储

用数组存储二叉树

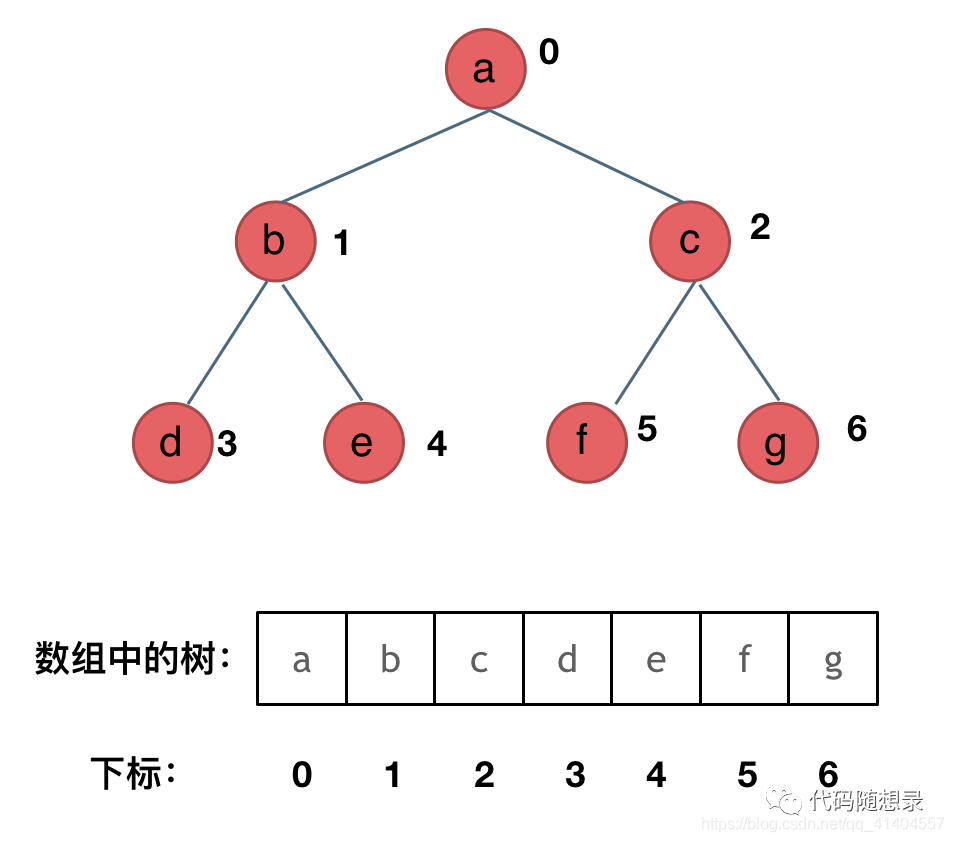
4.2.1数组存储的遍历

如果父节点的数组下标是i，那么它的左孩子就是\(2*i+1\)，右孩子就是\(2*i+2\)。

5.二叉树的遍历

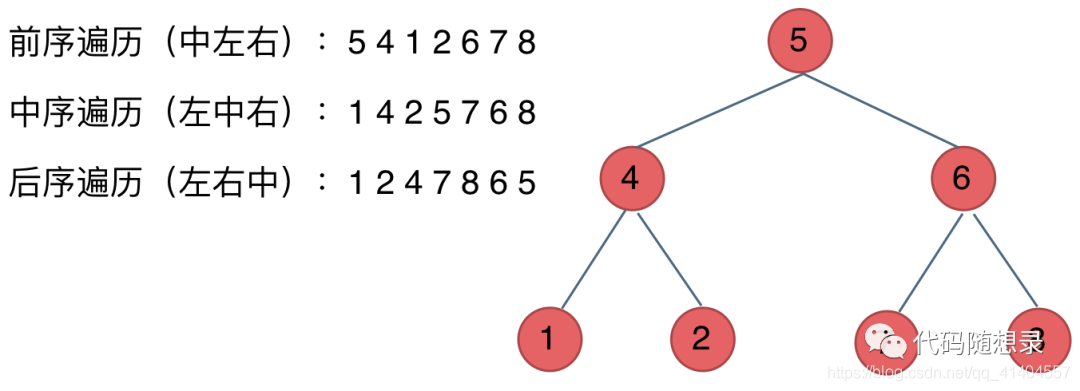
5.1深度优先遍历

1.前序遍历：中左中
2.中序遍历：左中左
3.后序遍历：左右中