河南萌新联赛2024第(三)场:河南大学
Circle
画出4个圈的交叉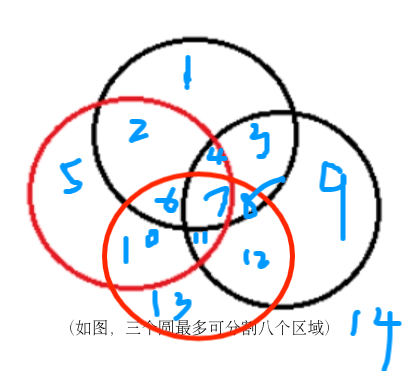
所以就是1 2 4 8 14,从第二个数开始,每个+2,+4,+6,....以此类推。
void solve()
{
int a[1000005]={0};
a[0]=1;
a[1]=2;
for(int i=2;i<1000005;i++)
{
a[i]=a[i-1]+2*(i-1);
}
int n; cin>>n;
while(n--)
{
int x; cin>>x;
cout<<a[x]<<" ";
}
}
keillempkill学姐の卷积
简单的模拟,但是注意细节的处理就行。
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
typedef pair<int,int> pii;
#define x first
#define y second
#define all(v) v.begin(),v.end()
#define allr(v) v.rbegin(),v.rend()
int dx[]={0,1,-1,0};
int dy[]={-1,0,0,1};
int a[25][25];
int b[25][25];
int ans[30][30];
int n,m;
int cal(int row,int line)
{
int temp=0;
for(int i=row,x=1;i<row+n,x<=n;i++,x++){
for(int j=line,y=1;j<line+n,y<=n;j++,y++)
{
temp+=a[x][y]*b[i][j];//注意这里a是放x,y而不是i,j
}
}
return temp;
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) cin>>a[i][j];
for(int i=1;i<=m;i++)
for(int j=1;j<=m;j++) cin>>b[i][j];
//外面两层循环是遍历每一个点
for(int k=1;k<=m-n+1;k++){
for(int g=1;g<=m-n+1;g++){
ans[k][g]=cal(k,g);
}
}
for(int i=1;i<=m-n+1;i++){
for(int j=1;j<=m-n+1;j++) cout<<ans[i][j]<<" ";
cout<<endl;
}
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0);
int t=1;
//cin>>t;
while(t--) solve();
//cout<<ans;
return 0;
}
SSH
多使用map来处理对应关系,边写边理清思路,有详细注释
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
typedef pair<int,int> pii;
#define x first
#define y second
#define all(v) v.begin(),v.end()
#define allr(v) v.rbegin(),v.rend()
int dx[]={0,1,-1,0};
int dy[]={-1,0,0,1};
void solve()
{
int n,m,q; cin>>m>>n>>q;//n台主机,m个密钥对,q次查询
map<string,string>key;//存公钥和私钥,左边si钥,右边公钥
for(int i=0;i<m;i++)
{
string pub,pri;
cin>>pub>>pri;
key[pri]=pub;
}
map<string,set<string> >user;//存用户和对应的密钥
map<string,set<string> >ipv4;//对应的ipv4的地址存的用户
for(int i=0;i<n;i++)
{
string ip; cin>>ip;//ip
int num;cin>>num;//有几个用户;
while(num--)
{
string name; cin>>name;//用户名
ipv4[ip].insert(name);//保存ip地址下的对应用户
int cnt ;cin>>cnt;//公钥数量
while(cnt--) {
string keyname;//公钥名称
cin>>keyname;
user[name].insert(keyname);//保存用户对应的公钥
}
}
}
//for(auto t:user["gg"]) cout<<t<<" ";
while(q--)
{
int f1=0,f2=0;
string name ;cin>>name;
string ip; cin>>ip;
string keyname;cin>>keyname;//私钥
if(ipv4[ip].find(name)!=ipv4[ip].end() ) f1=1;//用户名在对应ip的主机上
//用户拥有该私钥对应的密钥
string ans=key[keyname];
if(user[name].find(ans)!=user[name].end()) f2=1;
if(f1&&f2) cout<<"Yes";
else cout<<"No";
cout<<endl;
}
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0);
int t=1;
//cin>>t;
while(t--) solve();
//cout<<ans;
return 0;
}
求值
这题可以有二分的解法,也可以有三分的解法,但是三分的细节处理挺多的,我不是很会。使用二分的解法思路这么走:
1.\(∣x∗A+y∗B+z∗C−W∣\)与\(x+y+z=n\),我们可以发现\(z=n-x-y\),那么当你把z代入的时候就会有\((a-c)*x+(b-c)*y+n*c-w\),可以发现当我们枚举x,去二分y的时候,只要保证了\(b>c\),那么这个等式就可以满足单调性,所以在枚举x之前,处理b和c。
2.注意这里有一个绝对值,那么我们可以把找\(∣x∗A+y∗B+z∗C−W∣\),看成找\(x∗A+y∗B+z∗C−W>=0\)的最小值和找\(x∗A+y∗B+z∗C−W<=0\)的最大值(负数最大时,绝对值最小),都找完以后呢,再去取最小值。
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
typedef pair<int,int> pii;
#define x first
#define y second
#define all(v) v.begin(),v.end()
int dx[]={0,1,-1,0};
int dy[]={-1,0,0,1};
int a,b,c,n,w;
int cacl(int x,int y)//计算结果
{
return (a-c)*x+(b-c)*y+n*c-w;
}
void solve()
{
cin>>a>>b>>c>>n>>w;
if(b<c) swap(b,c);//保证b>c
int ans=1e19;
for(int i=0;i<=n;i++)//枚举x,去二分y
{
//找等式大于0时的最小值
int l=0,r=n-i;
int res=-1;
while(l<=r)
{
int mid=(l+r)>>1;//mid 相当于y,i相当于x
if(cacl(i,mid)>=0) res=cacl(i,mid),r=mid-1;
else l=mid+1;
}
int one=-1;
//找等式小于0时的最大值
l=0,r=n-i;
while(l<=r)
{
int mid=(l+r)>>1;
if(cacl(i,mid)<=0){
one=-cacl(i,mid);//要的是绝对值
l=mid+1;
}
else r=mid-1;
}
if(res!=-1) ans=min(ans,res);
if(one!=-1) ans=min(ans,one);
}
cout<<ans<<endl;
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0);
int t=1;
cin>>t;
while(t--) solve();
return 0;
}
累加器
这一题使用ymz的超级思路:对于每一个数从0到该数的二进制位的变化数为这个数除以每个二进制位的大小,举个例子:5,从0->5,二进制位对应为0101,那么使用到的二进制位的大小为4 2 1,所以变化次数为5/1+5/2+5/4=8次,样例1:1 4,1的变化次数为1,那么答案就是8-1=7。
总结:答案就是y+x的变化次数-y的变化次数
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
typedef pair<int,int> pii;
#define x first
#define y second
#define all(v) v.begin(),v.end()
int dx[]={0,1,-1,0};
int dy[]={-1,0,0,1};
int a[35];
void ycj()
{
a[0]=1;
for(int i=1;i<=32;i++) a[i]=a[i-1]*2;
}
void solve()
{
int xx,yy;cin>>xx>>yy;
yy+=xx;
int ans=0;
for(int i=0;i<=30;i++)
{
ans+=yy/a[i]-xx/a[i];
}
cout<<ans<<endl;
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0);
ycj();
int t=1;
cin>>t;
while(t--) solve();
return 0;
}
暴食之史莱姆
1.纯诈骗题,注意题目的几个条件,l是必须严格递减的,那么就必须从右往左遍历,并且如果异或要成为0的话只能是两个数是相同的,并且如果为0,或连续几个0也不增加操作次数,那么题意翻译一下,就是找有几个不为0的数字区间,比如5 1 0 2 2 4有3个区间,0不算。
/** - swj -
*
/>_____フ
| _ _|
/`ミ _x ノ
/ |
/ ヽ ?
/ ̄| | | |
| ( ̄ヽ__ヽ_)_)
\二つ
**/
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
typedef pair<int,int> pii;
#define x first
#define y second
#define all(v) v.begin(),v.end()
int dx[]={0,1,-1,0};
int dy[]={-1,0,0,1};
signed main()
{
ios::sync_with_stdio(false),cin.tie(0);
int n; cin>>n;
vector<int>a(n);
for(int i=0;i<n;i++) cin>>a[i];
//找有几个连续相同的区间且数不为0,不连续一个数为1个区间
vector<int>b;
for(int i=0;i<n;i++)
{
if(i==0||a[i]!=a[i-1]) b.emplace_back(a[i]);
}
cout<<b.size()-count(all(b),0);
}
游戏
1.对于1-n可以分两种情况,一种是在所有状态为1的边中从1到达了n,另一种是从状态为1的边中到达了k,再从状态为0或1的边从k到达n,那么这两种情况去取最小值即可。
/** - swj -
*
/>_____フ
| _ _|
/`ミ _x ノ
/ |
/ ヽ ?
/ ̄| | | |
| ( ̄ヽ__ヽ_)_)
\二つ
**/
#include <bits/stdc++.h>
#define int long long//要开longlong 不然过不去的
using namespace std;
using i64=long long;
typedef pair<int,int> pii;
map<pii,bool>mp;
struct DIJ{
using i64=long long;
using pii=pair<i64,i64>;
vector<i64>dis;//存点到点的最小距离
vector<vector<pii> >G;//存起点和终点的编号,边权
DIJ() {}//防止默认状态报错,类似vector<int>a,
//为dijkstra初始化
DIJ(int n)
{
dis.assign(n+1,1e17);//把所有元素设置为1e18
G.resize(n+1);//把G的大小设置为n+1
}
void add(int u,int v,int w){
G[u].emplace_back(v,w);//u v为点,w为边权
}
//堆优化版的dijkstra
void dijkstra(int s) {
priority_queue<pii> que;
dis[s] = 0;
que.push({0, s});
while (!que.empty()) {
auto p = que.top();
que.pop();
int u = p.second;
if (dis[u] < p.first) continue;
for (auto [v, w] : G[u]) {
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
que.push({ -dis[v], v});
}
}
}
}
};
signed main()
{
ios::sync_with_stdio(false),cin.tie(0);
int n,m,k; cin>>n>>m>>k;
vector<DIJ>dij(2,n);
for(int i=0;i<m;i++){
int u,v,w,t;
cin>>u>>v>>w>>t;
mp[{u,v}]=t;
if(mp[{u,v}]){
dij[1].add(u,v,w);
dij[1].add(v,u,w);
}
dij[0].add(u,v,w);
dij[0].add(v,u,w);
}
//这里跑全部状态为1的点,从点1到其他点的最短路
dij[1].dijkstra(1);
//这里跑状态为0,从k点出发到其他点的最短路
dij[0].dijkstra(k);
int ans1=dij[1].dis[n];
int ans2=dij[1].dis[k]+dij[0].dis[n];
if(ans1>=1e17&&ans2>=1e17) cout<<-1;
else cout<<min(ans1,ans2);
}
暴食之史莱姆
1.当我们只考虑一个编号为i的史莱姆左边可以吃多少个时,很明显,就是编号为i的史莱姆左边第一个比i体积小的史莱姆能吃的数量+1。那么右侧也是同理的,把数组翻转一下即可。答案便是左侧可以吃的+右侧可以吃的
2.使用单调栈来寻找左侧第一个比当前体积小的史莱姆,和右侧第一个比当前元素小的史莱姆,注意单调栈存下标,而不是当前元素的大小
/** - swj -
*
/>_____フ
| _ _|
/`ミ _x ノ
/ |
/ ヽ ?
/ ̄| | | |
| ( ̄ヽ__ヽ_)_)
\二つ
**/
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int,int> pii;
#define all(v) v.begin(),v.end()
signed main()
{
ios::sync_with_stdio(false),cin.tie(0);
int n; cin>>n;
vector<int>ve(n+1);
vector<int>ans1(n+1),ans2(n+1);
for(int i=1;i<=n;i++) cin>>ve[i];
//使用单调栈一般来说是放的下标
auto solve = [&](vector<int>&ans)->void{
stack<int>st;
for(int i=1;i<=n;i++){
while(!st.empty()&&ve[i]<ve[st.top()]) st.pop();//注意ve的下标
//!empty()要写在比较的左边,不然会出现越界,因为电脑会先判断是不是空的再去比较
if(!st.empty()) {
ans[i]=ans[st.top()]+1; //这里是ans[st.top()]+1
}
else ans[i]=0;
st.push(i);
}
};
solve(ans1);
reverse(ve.begin()+1,ve.end());
solve(ans2);
for(int i=1;i<=n;i++)
{
cout<<ans1[i]+ans2[n-i+1]<<" ";
}
}
posted on 2024-08-01 19:36 swj2529411658 阅读(43) 评论(0) 编辑 收藏 举报


