最短路

最短路算法框架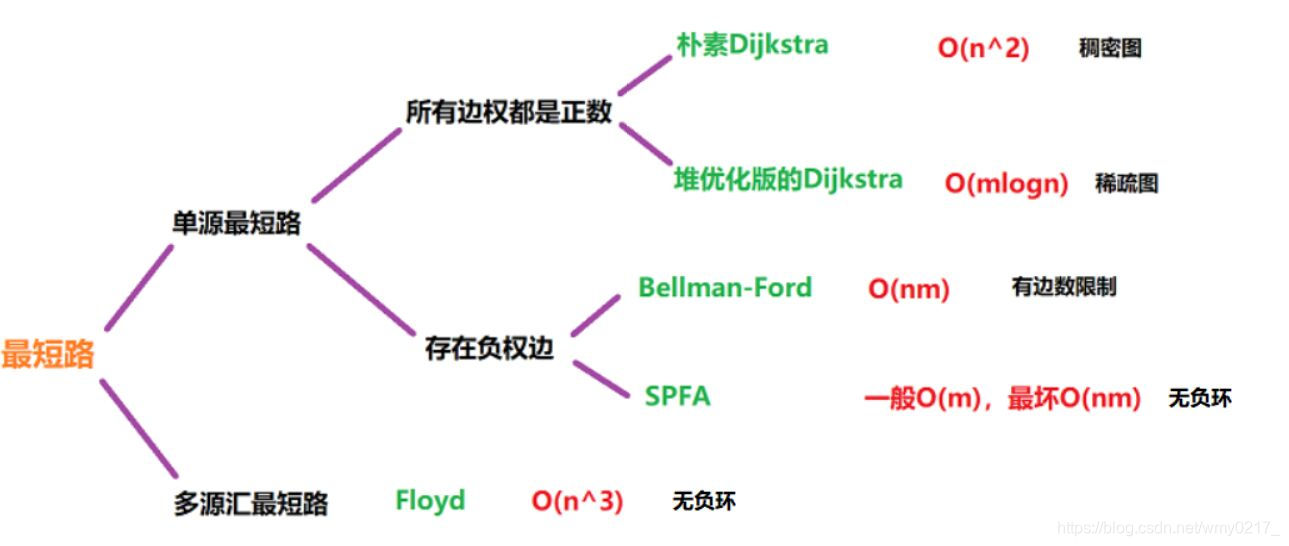

单源最短路：求一个点到其他点的最短路
多源最短路：求任意两点的最短路

稠密图用邻接矩阵存，稀疏图用邻接表来存。

稠密图：m和n²一个级别
稀疏图：m和n一个级别

dijkstra算法

朴素版

用来求一个源点到其他点的最短距离

#include <bits/stdc++.h>
using namespace std;
struct edge{
    int v;//边的终点
    int w;//边权
};

vector<edge>e[10005];
int dis[10005];//存u到源点x的最小距离
bool vis[10005];//标记是否选过
 int n,m,x;//节点数，边数，源点


//时间复杂度在O（n*n）
void dijkstra(int x)
{
    memset(dis,INT_MAX,sizeof dis);
    dis[x]=0;
   
    for(int i=1;i<n;i++){//枚举的次数
         int u=0;
        for(int j=1;j<=n;j++)//找到未标记过的且距离最小的点
        {
            if(!vis[j]&&dis[j]<dis[u]) u=j;
        }
        vis[u]=1;
        for(auto t:e[u])//遍历邻边
        {
            int v=t.v,w=t.w;
            if(dis[v]>dis[u]+w) dis[v]=dis[u]+w;//如果距离更小就更新
        }
    }
}



int main()
{
   
    cin>>n>>m>>x;
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        cin>>u>>v>>w;
        e[u].push_back({v,w});
    }
    dijkstra(x);
    cout<<dis[n];
}

堆优化版

#include <bits/stdc++.h>
#define int long long

using namespace std;
struct edge{
    int v;//边的终点
    int w;//边权
};

vector<edge>e[10005];
int dis[10005];//存u到源点x的最小距离
int vis[10005];//标记是否选过
 int n,m,x;//节点数，边数，源点
 
priority_queue<pair<int,int> >q;//大根堆,开小根堆去掉负号即可

//时间复杂度在O（m*logn）
void dijkstra(int x)
{
    for(int i=0;i<=n;i++) dis[i]=INT_MAX;
    dis[x]=0;
    q.push({0,x});
    while(q.size())
    {
        auto t=q.top(); q.pop();
        int u=t.second;
        if(vis[u]) continue;
        vis[u]=1;
        for(auto t:e[u])
        {
            int v=t.v,w=t.w;
            if(dis[v]>dis[u]+w) 
            {
            dis[v]=dis[u]+w;
            q.push({-dis[v],v});
              }
        }
        
    }
}



signed main()
{
    
    cin>>n>>m>>x;
    for(int i=1;i<=m;i++)
    {
        int u,v,w;
        cin>>u>>v>>w;
        e[u].push_back({v,w});
    }
    dijkstra(x);
    
    
}