125. 验证回文串--双指针
125. 验证回文串
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
示例 1:
输入: "A man, a plan, a canal: Panama" 输出: true
示例 2:
输入: "race a car" 输出: false
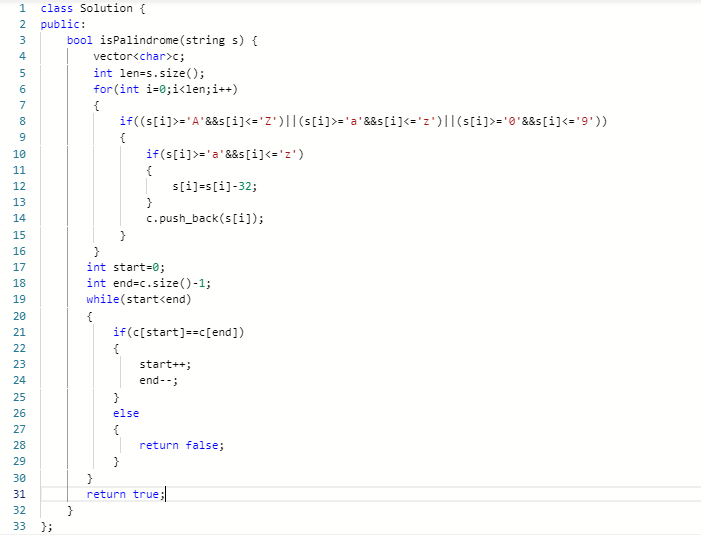
方法一:筛选 + 判断
最简单的方法是对字符串 ss 进行一次遍历,并将其中的字母和数字字符进行保留,放在另一个字符串 \textit{sgood}sgood 中。这样我们只需要判断 \textit{sgood}sgood 是否是一个普通的回文串即可。
判断的方法有两种。第一种是使用语言中的字符串翻转 API 得到 \textit{sgood}sgood 的逆序字符串 \textit{sgood\_rev}sgood_rev,只要这两个字符串相同,那么 \textit{sgood}sgood 就是回文串。
C++Python3Java
class Solution {
public:
bool isPalindrome(string s) {
string sgood;
for (char ch: s) {
if (isalnum(ch)) {
sgood += tolower(ch);
}
}
string sgood_rev(sgood.rbegin(), sgood.rend());
return sgood == sgood_rev;
}
};
第二种是使用双指针。初始时,左右指针分别指向 \textit{sgood}sgood 的两侧,随后我们不断地将这两个指针相向移动,每次移动一步,并判断这两个指针指向的字符是否相同。当这两个指针相遇时,就说明 \textit{sgood}sgood 时回文串。
C++Python3GolangJava
class Solution {
public:
bool isPalindrome(string s) {
string sgood;
for (char ch: s) {
if (isalnum(ch)) {
sgood += tolower(ch);
}
}
int n = sgood.size();
int left = 0, right = n - 1;
while (left < right) {
if (sgood[left] != sgood[right]) {
return false;
}
++left;
--right;
}
return true;
}
};
复杂度分析
时间复杂度:O(|s|)O(∣s∣),其中 |s|∣s∣ 是字符串 ss 的长度。
空间复杂度:O(|s|)O(∣s∣)。由于我们需要将所有的字母和数字字符存放在另一个字符串中,在最坏情况下,新的字符串 \textit{sgood}sgood 与原字符串 ss 完全相同,因此需要使用 O(|s|)O(∣s∣) 的空间。
方法二:在原字符串上直接判断
我们可以对方法一中第二种判断回文串的方法进行优化,就可以得到只使用 O(1)O(1) 空间的算法。
我们直接在原字符串 ss 上使用双指针。在移动任意一个指针时,需要不断地向另一指针的方向移动,直到遇到一个字母或数字字符,或者两指针重合为止。也就是说,我们每次将指针移到下一个字母字符或数字字符,再判断这两个指针指向的字符是否相同。
C++Python3GolangJava
class Solution {
public:
bool isPalindrome(string s) {
int n = s.size();
int left = 0, right = n - 1;
while (left < right) {
while (left < right && !isalnum(s[left])) {
++left;
}
while (left < right && !isalnum(s[right])) {
--right;
}
if (left < right) {
if (tolower(s[left]) != tolower(s[right])) {
return false;
}
++left;
--right;
}
}
return true;
}
};
复杂度分析
时间复杂度:O(|s|)O(∣s∣),其中 |s|∣s∣ 是字符串 ss 的长度。
空间复杂度:O(1)O(1)。
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/valid-palindrome/solution/yan-zheng-hui-wen-chuan-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。



