kmp字符串匹配
28. 实现 strStr()
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例 1:
输入: haystack = "hello", needle = "ll" 输出: 2
示例 2:
输入: haystack = "aaaaa", needle = "bba" 输出: -1
说明:
当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。
实现strStr( )---小白做法
解题思路
为大家推荐下面这个B站up主讲的KMP算法,超级好
kmp原理:https://www.bilibili.com/video/BV1Px411z7Yo?from=search&seid=13225444196686531503
kmp实现代码:https://www.bilibili.com/video/BV1hW411a7ys/?spm_id_from=333.788.videocard.0
代码
class Solution {
public:
int strStr(string haystack, string needle)
{
if(!needle.size()) return 0;
if(!haystack.size()) return -1;
//构造前缀表
int j = -1, i = 0;
vector<int> b(needle.size() + 1);
b[i] = j;
while(i < needle.size())
{
while(j >= 0 && needle[i] != needle[j]) j = b[j];
i++, j++;
b[i] = j;
}
//KMP-search
j = 0, i = 0;
while(j < haystack.size())
{
while(i >= 0 && needle[i] != haystack[j]) i = b[i];
i++, j++;
if(i == needle.size())
{
return j - needle.size();
}
}
return -1;
}
};KMP:花48小时看懂了KMP,想让你在48分钟内看懂 EL1S
点开了无数个KMP的讲解页面,点开文章中的各种跳转链接,居然被我发现了这样一篇好文章,代码写的好短,还有图:https://www.inf.hs-flensburg.de/lang/algorithmen/pattern/kmpen.htm 结合自己的理解分享一下。
一、KMP的用途,作用对象
第一个问题:KMP是干嘛用的?
KMP是用来找字符串匹配的
第二个问题:为什么要用KMP来找字符串匹配?
KMP的时间复杂度是O(m + n),时间复杂度低
我们拿一道题来做例子Leetcode28.实现 strStr()
这道题能想到几种方式?
第一种:遍历haystack的每一个字符作为开头,needle.size()为长度和needle做对比,一样则返回这个开头的idx
第二种: 枚举haystack的每一个字符作为开头,neddle.size()作为长度,扔到map<string, int>里面,去map里面找有没有needle
第三种:本文介绍的KMP
KMP的两个对象是什么:
第一个:pattern->也就是题目中的needle
第二个:text->也是就是题目中的haystack
二、KMP的流程要分为两步:
第一步:构建一个数组b,大小是pattern.size() + 1,进行Preprocess预处理对数组填充
第二步:把pattern和text进行匹配,利用b数组加速匹配,找到那个出现的第一个位置的idx
2.1 构建数组b
在构建b数组之前,要让你们认识到b数组的必要性,也是就是它到底能怎么帮助我们加速匹配?
text: ababbabaa
pattern: ababac
不用加速的时候是这样的(绿的匹配上了,红的匹配失败,黑的还没匹配):
每次遇到不匹配的时候呢,头部就往右边挪一个位置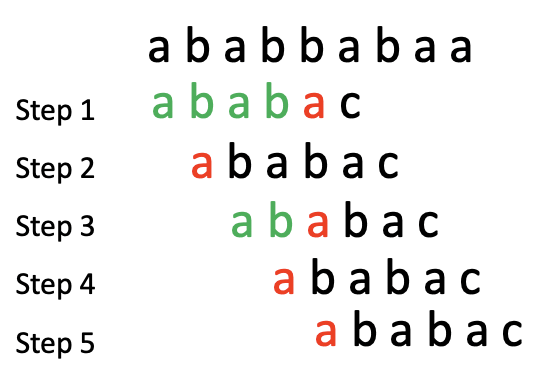
用加速的时候是这样的:
每次遇到不匹配挪动的位置可能就不止一步了! 注意注意:不止一步不止一步!!上面那个是慢走大路,这个就是抄近路。这里上面的图和下面的图我都是画了5个step,似乎并没有加速?这个例子呢是因为字符长度比较短,对于字符串长度长的效果会很明显。
下面这张图我是为了说明两个道理:1. 它不是一步一步的挪动的,是跳着挪动的!所以会快,因为不用匹配那么多次了呀;2. 而且仔细看,下面这些图有一些红色之前还是黑色!这些也是没有去重复匹配的,但是上面的图红色之前都是绿色,说明都有遍历匹配!
好了,现在我们知道是可以这样加速的,我们就有加速的rules!这些rules就存在前文提及到的数组b里面,也是就是说啊,当我pattern和text发生不匹配的时候啊,我要怎么往前跳一下?
现在我们的问题是怎么构建这个数组b?
让我们先来观察一下这个跳动是怎么跳的,为什么要这样跳?
一开始的时候是text[0-3] = "abab" 匹配上了pattern[0-3] = "abab",但是在text[4]和pattern[4]匹配的时候发现了不匹配,可惜之前匹配了那么一大串了,于是就有一个想法:能不能把之前匹配过的利用起来?
我们把pattern进行滑动看看效果: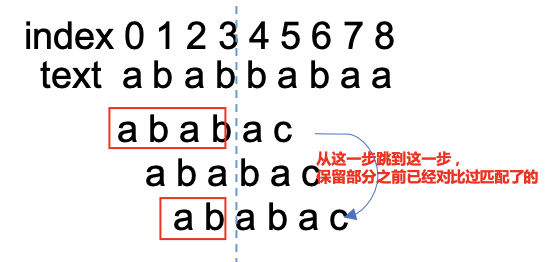
这张图应该让你明白是想要怎么保留利用之前匹配过了的,那么现在该看看这个b怎么建立了
b这个数组的大小是pattern.size() + 1,数组里面存的东西的含义是,假设text[k]和pattern[i]没有匹配上,i要进行更新,更新成i = b[i], 然后再去text[k]和pattern[i]进行对比。
建立这个b的代码是:
int j = -1, i = 0;//j在后面,i在前面
vector<int> b(needle.size() + 1);
b[i] = j;
while(i < needle.size())
{
while(j >= 0 && needle[i] != needle[j]) j = b[j];
i++, j++;
b[i] = j;
}
我给一个例子,搭配着图解释:
一开始,把j初始化为-1, i初始化为0,b[0]初始化为-1,为什么要这样初始化后面会讲,先跳过看一下效果。
j >= 0不成立,所以没有进入while循环,i++ = 1 j++ = 0 b[1] = 0;是不是看了这波操作有一点懵圈?让我来理一下思路,这段代码在填充b的时候就是:背靠着山,未雨绸缪。意思是i = 0先保证了自己的匹配成功,然后去为i = 1考虑:若pattern在i = 1的时候和text匹配不上了,保留一段已经匹配过的,然后让pattern的哪个idx的字符接着和text去匹配
看回我们之前的例子: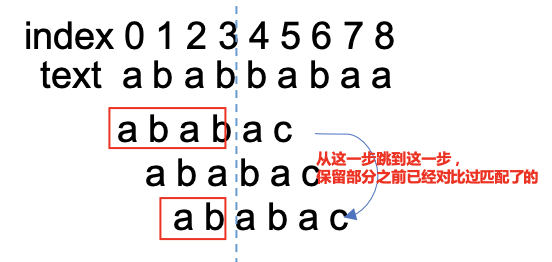
这里不就是i = 4的时候pattern和text匹配不上了,然后pattern保留了一段(即"ab"),然后让pattern idx = 2的字符接着和text进行匹配
再来看看我们现在这个例子:
就是i = 0的时候就去为i = 1做打算,如果说pattern[i = 1]和text不匹配了,i就不能是1了该变到几?答案是0,去和pattern[i = 0]匹配吧
这两个指针i, j,会努力维持pattern[i] = pattern[j],如果实在维持不了的话,j就是-1了; 因为代码里面有那个i++, j++,所以下一个i = 1其实要是j = 0去匹配
继续看,现在是i = 1,j = 0,发现居然匹配不上,j很生气,就往左边跑,j = b[j = 0] = -1,然后i++ = 2, j++ = 0, 这里就是当i = 1的时候在为i = 2考虑啊了,i = 1先把自己匹配上,匹配不上j就到-1,然后i = 1告诉i = 2:b[2] = 0,意思是i = 2啊要是你pattern[i = 2]没有和text匹配上的话你去pattern[b[2]] = pattern[0]看看能不能匹配上。
下一步是i = 2, j = 0;哈哈哈,有意思,我pattern[i]和pattern[j]一样的,于是i = 2告诉i = 3:我i = 2是匹配了成了的,你要是没和text匹配上,你就去和pattern[j + 1 = 1]匹配吧,因此b[i = 3] = j + 1 = 1
再下一步,i = 3, j = 1;pattern[i] = pattern[j],匹配上了哦,i = 3告诉i = 4: b[i= 4] = j + 1 = 2
接着,i = 4, j = 2, pattern[i] = pattern[j],嗯,很好,i = 4自己匹配上了,于是告诉i = 5: 你要是没和text匹配上啊你就和pattern[3]匹配去吧,故b[i = 5] = 3
到了i = 5, j = 3; i = 5要让自己先匹配,然后为i = 6做打算,呀pattern[i]和pattern[j]居然不匹配,说明啊,i = 5得找到前面的一个j和自己有相同的prefix这样呢,才能为i = 6做打算,那么怎么找前面的j呢?i = 5心里思考:i= 4和我说了要是我匹配不上的话我可以往前, b[j = 3] = 1,于是i = 5就去和pattern[j = 1]做这个对比了,发现还不一样,只好再往前了,j = b[j = 1] = 0, pattern[0] = 'a' = pattern[5],好了终于相同了,可以为i = 6做谋划了,i = 6就是要走i = 5的后尘下一步,b[6] = j + 1 = 0 + 1 = 1
2.2 利用数组b
b数组构建好了,到了KMP的第二大步骤了:把b数组用起来!
j = 0, i = 0; //j这回是text的, i是pattern的
while(j < haystack.size())
{
while(i >= 0 && needle[i] != haystack[j]) i = b[i];
i++, j++;
if(i == needle.size())
{
return j - needle.size();
}
}
return -1;
i是指向pattern的指针,j是指向text的指针,如果text[j] == pattern[i],那就i++, j++继续向后比对就是了,
如果text[j] != pattern[i]呢,这个时候就是pattern开始跳跃的时候了, text[j] != pattern[i]是吧,pattern说:那我看看我的rules记录本b,b[i]告诉我我要跳到这个位置,好,于是i = b[i]; text[j]再和pattern[i]比过,如果相同那么就继续向后,不过不同,那i继续向前跳,如果i都跳到-1了都没有找到pattern[i] = text[j],说明啊这个text[j]我的pattern的前缀里面就是没有合适的,那行吧,j你加一吧,我i从0开始重新开始匹配。
三、题目KMP解法代码
class Solution {
public:
int strStr(string haystack, string needle) {
if(!needle.size()) return 0;
if(!haystack.size()) return -1;
//先构造pattern
int j = -1, i = 0;//j在后面,i在前面
vector<int> b(needle.size() + 1);
b[i] = j;
while(i < needle.size())
{
while(j >= 0 && needle[i] != needle[j]) j = b[j];
i++, j++;
b[i] = j;
}
j = 0, i = 0; //j这回是text的, i是pattern的
while(j < haystack.size())
{
while(i >= 0 && needle[i] != haystack[j]) i = b[i];
i++, j++;
if(i == needle.size())
{
return j - needle.size();
}
}
return -1;
}
};


