poj1182 带权并查集

食物链

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 60225		Accepted: 17656

Description

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是"1 X Y"，表示X和Y是同类。
第二种说法是"2 X Y"，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1）当前的话与前面的某些真的话冲突，就是假话；
2）当前的话中X或Y比N大，就是假话；
3）当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。

Input

第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。

Output

只有一个整数，表示假话的数目。

Sample Input

思路:

根据题意，可以肯定的是一个一题关于集合的题目，所以考虑并查集处理。由于这里并不是直接的种类，然后动物。所以给可以给当前的动物和他的父亲之间一个值来表示关系。

现在pa[i]表示i的,rel[i]表示pa[i] 和 i的关系。rel[i] = 0表示为同一类，1表示i可以吃i吃pa[i]，2表示pa[i] 吃 i。

对于输入的x,y。先找到他们所在集合的祖先，也就是pa[i]（因为路径压缩了，所以pa[i]不是表示i的父亲）。fx=pa[x],fy=pa[y]。

1.如果fx == fy说明这x,y之前已经处理过，已经在同一个集合之中。只要判断他们2个在集合中的关系就好。

如图所示，现在x=3,y=4,x y已经在同一个集合中，现在要根据已经知道的rel[3],rel[4]，来得到3和4的关系。不过先要知道3 - rel[4]就是图中1到4的箭头，由于传递性，3到4的关系就是(rel[3] + 3 - rel[4]) % 3，这样就可以得到3 4之间的关系，根据这个关系来判断是否这句话正确。

2.如果x,y不在同一个集合中。说明这句话是对的，同时我们需要对值进行更新维护。我在这里更新都是pa[fy] = fx;

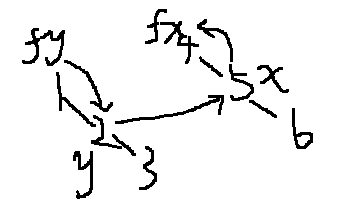
如图所以现在x = 2,y = 5，x,y不在同一个集合中。这时候我把pa[fy] = fx,这样的话我要更新的是rel[fy]，此时rel[fy] = (3 - rel[y] + j + rel[x]) % 3，这里的j是根据d来的，如果d=1，那么j = 0,因为同类，如果d = 2，那么j = 2，因为x 能够吃 y,所以y 和 x的关系为2。

这样就完成了2个集合的合并。

现在还有一部就是路径压缩时候也要更新，维护rel的值。很简单，因为递归，先更新了pa[x]，这时候rel[pa[x]]更新了,rel[pa[x]]为pa[x]指向集合根节点的rel值了。所以rel[x] = (rel[x] + rel[pa[x]]) % 3。这样问题就解决了。

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<string>
#include<time.h>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define INF 1000000001
#define ll long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
const int MAXN = 50010;
int pa[MAXN],n,k,rel[MAXN];
void Init()
{
    for(int i = 0; i <= n; i++){
        pa[i] = i;
    }
    memset(rel,0,sizeof(rel));
}
int find(int x)
{
    if(x != pa[x]){
        int fx = find(pa[x]);
        rel[x] = (rel[x] + rel[pa[x]]) % 3;
        pa[x] = fx;
    }
    return pa[x];
}
int main()
{
        scanf("%d%d",&n,&k);
        Init();
        int d,x,y;
        int ans = 0;
        while(k--){
            scanf("%d%d%d",&d,&x,&y);
            if(x > n || y > n){
                 ans ++;
            }
            else if(d == 2 && x == y){
                ans ++;
            }
            else if(d == 1){
                int fx = find(x);
                int fy = find(y);
                if(fx == fy){
                    int ret = (rel[x] + 3 - rel[y]) % 3;
                    if(ret != 0){
                        ans ++;
                    }
                }
                else {
                    pa[fy] = fx;
                    rel[fy] = (3 - rel[y] + rel[x]) % 3;
                }
            }
            else {
                int fx = find(x);
                int fy = find(y);
                if(fx == fy){
                    int ret = (rel[x] + 3 - rel[y]) % 3;
                    if(ret != 1){
                        ans ++;
                    }
                }
                else {
                    pa[fy] = fx;
                    rel[fy] = (5 - rel[y] + rel[x]) % 3;
                    rel[fy] = rel[fy];
                }
            }
            //cout<<ans<<endl;
        }
        printf("%d\n",ans);
    return 0;
}

posted @ 2016-05-09 15:36 sweat123 阅读(243) 评论(0) 编辑收藏举报

刷新页面返回顶部

sweatOtt

加油

poj1182 带权并查集

公告