[Fundamental of Power Electronics]-PART II-9. 控制器设计-9.4 稳定性

9.4 稳定性

众所周知的是，增加反馈回路可能会导致原本稳定的系统变得不稳定。尽管原变换器传递函数(式(9.1))以及环路增益\(T(s)\)不包含右半平面极点，但式(9.4)的闭环传递函数仍然可能存在右半平面极点。那么之后，反馈回路将无法调节到所需的静态工作点，并且可能会观察到振荡出现。避免这种情况是非常重要的。即便反馈系统是稳定的，其瞬态响应也可能会出现不希望的振铃和过冲。本节讨论了系统稳定性的问题，并介绍了一种确保反馈系统稳定且特性较好的方法。

当反馈使得系统不稳定时，式(9.4)的分母项\((1+T(s))\)包含右半平面的根(也就是具有正实部)。如果\(T(s)\)是有理分数，也就是多项式函数\(N(s)\)和\(D(s)\)的比值\(N(s)/D(s)\)。那么我们可以写出：

\[\begin{aligned} & \cfrac{T(s)}{1+T(s)}=\cfrac{\cfrac{N(s)}{D(s)}}{1+\cfrac{N(s)}{D(s)}}=\cfrac{N(s)}{N(s)+D(s)} \\ & \cfrac{1}{1+T(s)}=\cfrac{1}{1+\cfrac{N(s)}{D(s)}}=\cfrac{D(s)}{N(s)+D(s)} \end{aligned} \tag{9.20} \]

因此，\(T(s)/(1+T(s))\)和\(1/(1+T(s))\)具有相同的极点，也就是多项式\(N(s)+D(s)\)的根。稳定性的暴力测试就是分析\(N(s)+D(s)\)，对结果进行因式分解，来确定是否有正实数的根。然而，除了一些非常简单的环路增益以外，这将带来大量的工作。奈奎斯特稳定性定理给出了一种更具有启发性的方法，其中\(N(s)+D(s)\)的右半平面的根的数目可以通过对\(T(s)\)的测试来确定。这个定理将在9.4.2节中进行讨论。通常，这个定理的一个特例也就是相位裕度的分析就足以设计大多数稳压器。接下来让我们首先讨论更为简单的相位裕度问题。

9.4.1 相位裕度测试

穿越频率\(f_{c}\)被定义为环路增益幅值为1时的频率：

\[||T(j2\pi f_{c})||=1 \Rightarrow 0\ dB \tag{9.21} \]

为了计算相位裕度\(\varphi_{m}\)，在穿越频率处求解环路增益\(T\)的相位，并将其加上180°：

\[\varphi_{m}=180°+\angle{T}(j2\pi f_{c}) \tag{9.22} \]

如果恰好只有一个穿越频率，并且环路增益\(T(s)\)不包含右半平面极点，并且式(9.22)的值为正的，那么\(1/(1+T)\)和\(T/(1+T)\)都是不包含右半平面极点的。因此，对\(T(s)\)进行一个简单的测试，就可以确定\(T/(1+T)\)和\(1/(1+T)\)的稳定性。这是一个非常易用的设计工具，我们只需要保证在穿越频率下\(T\)的相位大于-180°即可。

当存在多个穿越频率时，相位裕度的测试可能会出现不必要歧义。并且，当\(T\)包含右半平面极点时(也就是原始开环系统不稳定)，就不能使用相位裕度来测试了。无论什么情况，都要使用更通用的奈奎斯特稳定定理来分析。

一个典型稳定系统的环路增益如图9.9所示。可以看到\(\angle T(j2\pi f_{c})=-112°\)。因此，\(\varphi_{m}=180°-112°=+68°\)。由于相位裕度为正，\(T/(1+T)\)和\(1/(1+T)\)没有右半平面极点，并且反馈系统是稳定的。

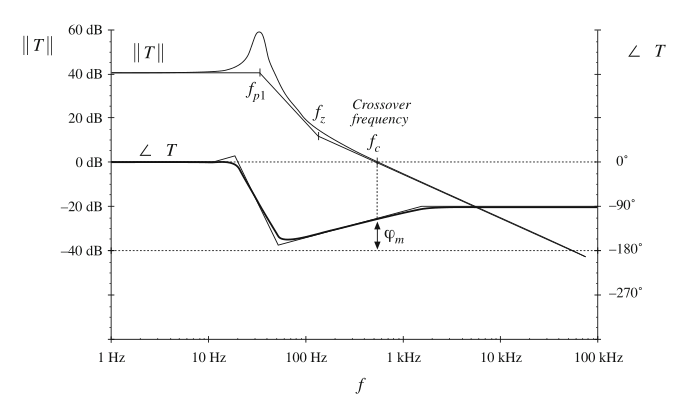
Fig. 9.9 Magnitude and phase of the loop gain of a stable system. The phase margin \(\varphi_{m}\) is positive

如图9.10所示为一个不稳定系统的环路增益。这个例子中，\(\angle T(j2\pi f_{c})=-230°\)。相位裕度为\(\varphi_{m}=180°-230°=-50°\)。负的相位裕度意味着\(T/(1+T)\)和\(1/(1+T)\)各自包含至少一个右半平面极点。

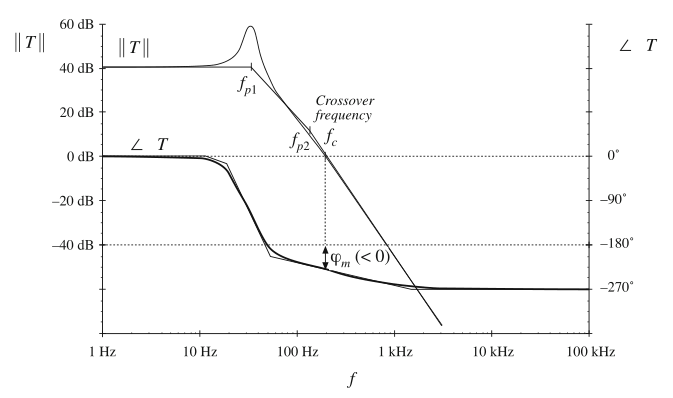
Fig. 9.10 Magnitude and phase of the loop gain of an unstable system. The phase margin \(\varphi_{m}\) is negative

9.4.2 奈奎斯特稳定判据

奈奎斯特稳定判据是一种严格的通用技术，其可以根据闭环系统的环路增益来评估其稳定性。基于环路增益\(T(s)\)的图，可以从其bode图中确定位于闭环传递函数\(T/(1+T)\)和\(1/(1+T)\)在右半平面的极点数。9.4.1节中的相位裕度测试是基于奈奎斯特图的，它是有用的，但又不是完全通用的方法。在某些情况下，包括本书后面将会遇到的几个示例，必须采用更为一般的奈奎斯特稳定测试方法。

奈奎斯特稳定判据是基于曲线\(\Gamma\)的保形映射，这个曲线\(\Gamma\)包围了复平面的右半平面(正实数部分)。闭合曲线是通过环路增益传递函数\(T(s)\)映射而来的。通过映射后的曲线对\((-1,0)\)点的包围情况可以计算闭环传递函数中存在的右半平面极点的数量。在下面的小节中提供了衍生的工具，准确的应用规则以及一些重要的实例。

理论分析原理

让我们来考虑一个零点在\(s=s_{1}\)的传递函数\(T(s)\)：

\[T(s)=(s-s_{1}) \tag{9.23} \]

让我们再来考虑如图9.11a所示的围绕点\(s_{1}\)的\(s\)复平面上的闭合曲线\(\Gamma\)。复变量\(s\)随路径\(\Gamma\)变化，从点a开始，围绕曲线沿顺时针方向经过点b，c最后回到a。对于式(9.23)中的例子\(T(s)\)，\(T(s)\)在某点\(s\)处的值被看做是从\(s_{1}\)指向\(s\)的向量，其幅值和相位如图9.11a所示。

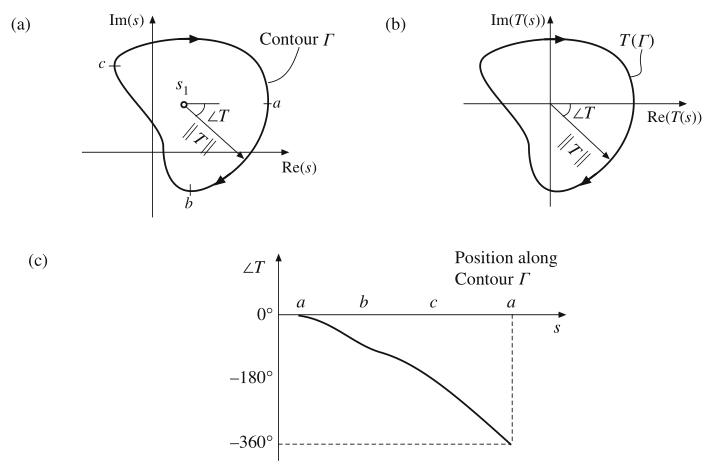
Fig. 9.11 Principle of the argument, example 1: (a) a closed contour Γ in the complex s plane, (b)
mapping of the contour Γ through the transfer function T(s) o f Eq.(9.23), (c) variation of the phase of T(s), as s varies around the contour Γ

如图9.11c所示，\(s=a\)时相角\(\angle T\)为0°。当\(s\)沿着曲线移动时，经过b，c，最后回到a，相角\(\angle T\)减小，并且经过移动一周后，相位变为-360°。这里，净相位变化为-360°，表明\(s_{1}\)处的零点位于曲线\(\Gamma\)内。

图9.11b包含了\(T(s)\)沿\(\Gamma\)曲线随\(s\)变化的图形；幅值\(||T||\)和相角\(\angle T\)的量与图9.11a中标识的相同。这个图形就是通过传递函数\(T(s)\)的保形映射；保形映射保留相角信息。正如\(\angle T(s)\)的-360°的净变化，映射曲线\(T(\Gamma)\)包围了\(T(s)\)平面的原点。

图9.12a描绘了不包围\(T(s)\)在\(s_{1}\)处零点的第二条曲线\(\Gamma^{'}\)。如图9.12c所示，经过对曲线\(\Gamma^{'}\)的一周完全移动后，\(\angle T\)的净变化量为0。映射后曲线\(T(\Gamma^{'})\)如图9.12b所示，这个曲线不包含\(T(s)\)平面的原点。

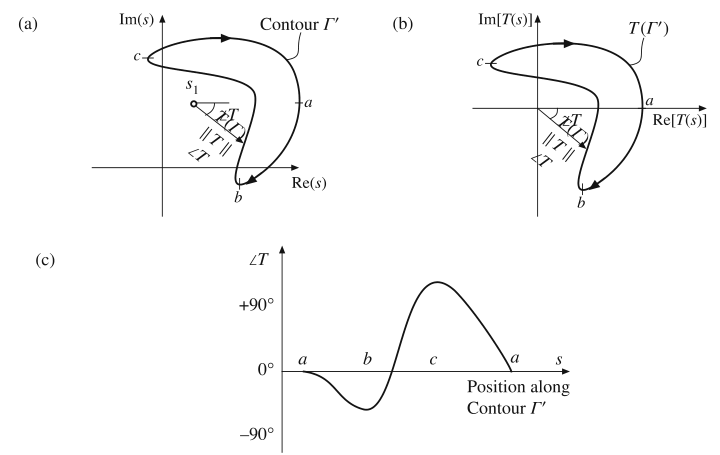
Fig. 9.12 Principle of the argument, example 2: (a) a closed contour \(\Gamma^{’}\) in the complex s plane, (b)
mapping of the contour \(\Gamma^{’}\) through the transfer function T(s) o f Eq.(9.23), (c) variation of the phase of T(s), as s varies around the contour \(\Gamma^{’}\). Since the zero at \(s = s_1\) does not lie inside contour \(\Gamma^{’}\), there is no net change in the phase of T, and the mapped contour \(T(\Gamma^{’})\) does not encircle the origin of the T plane

复变函数的相角通常称为幅角。Cauchy幅角原理告诉我们，当闭合曲线包围零点\(s_{1}\)时，随着\(s\)沿着\(\Gamma\)顺时针走一圈，\(\ang T(s)\)的净变化量为-360°。这与映射曲线\(T(\Gamma)\)包含原点是等效的。(译者：此处具体参考幅角原理)

接下来让我们考虑包含多个极点和零点的传递函数\(T(s)\)：

\[T(s)=T_{ref} \cfrac{(s-z_{1})(s-z_{2})...}{(s-p_{1})(s-p_{2})...} \tag{9.24} \]

像往常一样，我们可以将\(T(s)\)的相位表示为每个零点或极点产生的各项的相角之和。如下所示：

\[\begin{aligned} & \ang T(s)=\ang(s-z_{1})+\ang(s-z_{2})+... \\ &\ \ \ \ \ \ \ \ \ \ \ -\ang(s-p_{1})+\ang(s-p_{2})+... \end{aligned} \tag{9.25} \]

我们可以再次在\(s\)复平面上定义一个闭合曲线\(\Gamma\)，并且分析\(T(s)\)的相位在\(s\)沿顺时针方向经过曲线一周的变化情况。每一个位于曲线内的\(T(s)\)的零点将会导致\(\ang T\)的净变化为-360°，并且每一个位于曲线内的\(T(s)\)的极点导致的\(\ang T\)的净变化为+360°。如果总计有\(Z\)个零点和\(P\)个极点位于曲线\(\Gamma\)内，那么\(\ang T\)的净变化为\(-N*360°\)，其中：

\[N=Z-P \tag{9.26} \]

映射曲线\(T(\Gamma)\)将顺时针包围\(T(s)\)平面的原点\(N\)圈。

那么幅角原理就为我们提供了一种可以确定曲线\(\Gamma\)内零极点数量的工具。

Nyquist 曲线

我们期望确定式(9.20)所示的闭环传递函数是否存在位于右半复平面的不稳定极点。为此，我们可以定义一个包围整个右半平面的曲线\(\Gamma\)，然后利用幅角原理来确定这个曲线包含的闭环极点的数目。

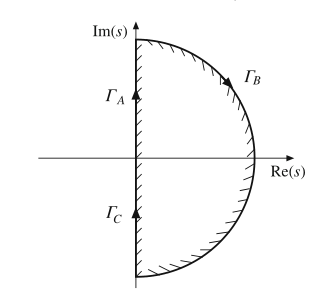
Fig. 9.13 The Nyquist contour, which encloses the right half of the complex s plane

图9.13所示的曲线\(\Gamma\)被称为Nyquist曲线。沿顺时针方向遍历这个曲线，曲线右侧的封面封闭区域就是\(s\)平面的右半部分。Nyquist曲线包含三个部分。线段\(\Gamma_{A}\)是虚轴的正半部分，其中：

\[s=j\omega\ with\ \ \omega \in(0,\infty) \tag{9.27} \]

可以将\(\Gamma_{B}\)选择为位于所有闭环极点右侧的半圆弧，其定义如下：

\[s=Re^{j\theta} \ with\ R \rightarrow \infty\ \ and\ \ \theta \in(+90°,-90°) \tag{9.28} \]

\(\Gamma_{C}\)是虚轴的负半部分，其中：

\[s=-j\omega\ with\ \ \omega \in(\infty,0) \tag{9.29} \]

如果传递函数\(F(s)\)在复平面右半平面上包含\(Z\)个零点和\(P\)个极点，那么Nyquist的映射曲线\(F(\Gamma)\)将包围\(F(s)\)平面的原点\(N=(Z-P)\)次。

稳定性分析

如式(9.20)的闭环传递函数包含分母多项式为\(N(s)+D(s)\)，其根为闭环传递函数的极点。我们希望确定这个多项式是不是包含\(s\)复平面的右半平面的根。从式(9.20)又可以看出，这些根就是\((1+T(s))\)的零点，此外，\((1+T(s))\)的极点与\(T(s)\)的极点是一致的。因此，我们还可以通过传递函数\((1+T(s))\)来映射图9.13所示的Nyquist曲线，并且来评估包围原点的圈数。

在复平面内，\((1+T(s))\)就相当于\(T(s)\)向右平移了一个单位。如果映射的曲线\((1+T(\Gamma))\)包围原点，那么曲线\(T(\Gamma)\)就包围\((-1,0)\)点。因此，我们可以利用环路增益\(T(s)\)来映射图9.13所示的Nyquist曲线，并且来计算\(T(\Gamma)\)包围\((-1,0)\)的圈数来计算\(N\)。根据\(N=Z-P\)，环绕圈数\(N\)与右半平面极点数有关，其中\(Z\)是闭环增益\(T/(1+T)\)或者\(1/(1+T)\)的右半平面极点数；\(P\)是原环路增益\(T(s)\)中存在的右半平面极点数。

如果原始开环系统是稳定的，那么\(T(s)\)不包含右半平面极点，也就是\(P=0\)。在这种常见的\(N=Z\)情况下，\((-1,0)\)点被\(T(\Gamma)\)曲线包围的圈数就等于\(T/(1+T)\)或\(1/(1+T)\)的闭环右半平面极点数。

一个基础示例

作为第一个例子，让我们来考虑含有三个极点的环路增益\(T(s)\)：

\[T(s)=\cfrac{T_{0}}{(1+\cfrac{s}{\omega_{1}})(1+\cfrac{s}{\omega_{2}})(1+\cfrac{s}{\omega_{3}})} \tag{9.30} \]

图9.14给出了一组特定\(T_{0},\omega_{1},\omega_{2},\omega_{3}\)的值情况下，\(T(s)\)的幅值和相角的bode图。在这个例子中，\(T(s)\)在穿越频率\(\omega_{c}\)处的相角裕度为\(\varphi_{m}\)。

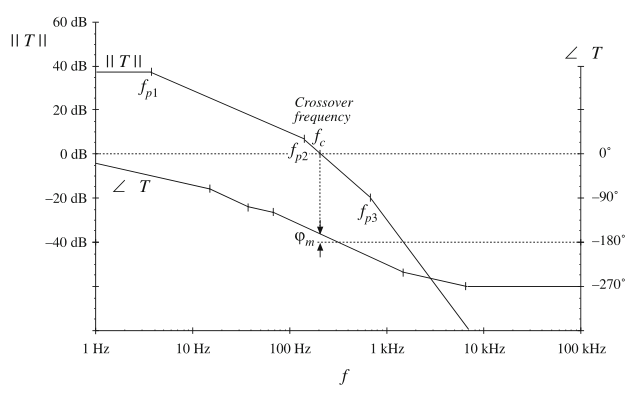
Fig. 9.14 Bode plot of loop gain T(s) for the example of Eq. (9.30)

图9.15a描绘了Nyquist图的第一部分，其为式(9.27)定义的\(\Gamma_{A}\)经环路增益映射后的结果。因为沿着\(\Gamma_{A}\)且\(s=j\omega\)，这就对应了\(T(j\omega)\)的极坐标图，其与图9.14给出bode图中的幅值和相位数据是保持一致的。在\(\omega=0\)时，环路增益的幅值为\(T_{0}\)并且相角为0°，因此Nyquist图开始于正实轴上的\(T=T_{0}\)。随着\(\omega\)的增加，如图所示，其幅值减小，相位变为负值。

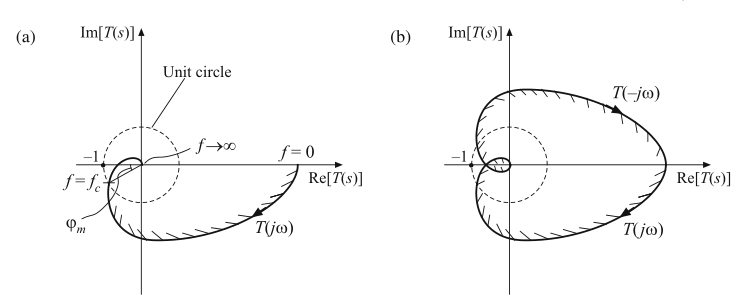
Fig. 9.15 Nyquist plot for the loop gain of Fig.9.14: (a) mapping of the contour \(Γ_A\) through the loop gain T(s), (b) mapping of the complete Nyquist contour through the loop gain T(s)

在穿越频率频率\(f_{c}\)处，环路增益的幅值为1，相角为\((-180°+\varphi_{m})\)。如图9.15a所示，曲线\(T(j\omega)\)在这一点穿越单位圆。在高于\(f_{c}\)的频率，幅值继续减小，曲线\(T(j\omega)\)趋向于原点。

Nyquist曲线的第二部分为式(9.28)定义的\(\Gamma_{B}\)。为了分析环路增益\(T(s)\)如何映射曲线\(\Gamma_{B}\)，我们首先将\(s=Re^{j\theta}\)代入式(9.30):

\[T(Re^{j\theta})=\cfrac{T_{0}}{(1+\cfrac{Re^{j\theta}}{\omega_{1}})(1+\cfrac{Re^{j\theta}}{\omega_{2}})(1+\cfrac{Re^{j\theta}}{\omega_{3}})} \tag{9.31} \]

接下来，让我们令\(R \rightarrow\ \infty\)。这使得式(9.31)的分母在幅值上趋向于无穷，这就使得了\(T\)的幅值趋向于0。Nyquist图的这部分趋向于原点。Nyquist图的第三部分就是通过环路增益\(T(s)\)对式(9.29)定义的\(\Gamma_{C}\)的映射。Nyquist曲线中的这一部分就是\(T(-j\omega)\)的极坐标图，它是\(T(j\omega)\)的复共轭。因此，如图9.15b所示，通过将\(T(j\omega)\)沿实轴对称就可以很容易得到这个图形。

现在我们可以来确定(-1,0)点被\(T(\Gamma)\)包围的圈数。对图9.15b的观察发现，(-1,0)点并没有被包围于曲线\(T(\Gamma)\)的内部，因此，包围圈数为0：\(N=0\)。由于原环路增益\(T(s)\)不包含右半平面极点，因此\(P=0\)。根据式(9.26)，\(Z=0\)，所以闭环传递函数不包含右半平面极点，反馈环路是稳定的。

如果图9.14中的相角裕度\(\varphi_{m}\)是负值，那么曲线\(T(\Gamma)\)将会如图9.16所示。\(T(j\omega)\)将在第三象限中穿越单位圆。在这种情况下，图9.16b的Nyquist曲线包围(-1,0)点两次：\(N=2\)。因此\(Z=2\)，闭环传递函数有两个右半平面极点。反馈环路是不稳定的。在这个例子中，原\(T(s)\)包含三个左半平面极点；在闭环传递函数\(T/(1+T)\)中，其中两个极点移动到了右半平面，一个极点留在了左半平面。

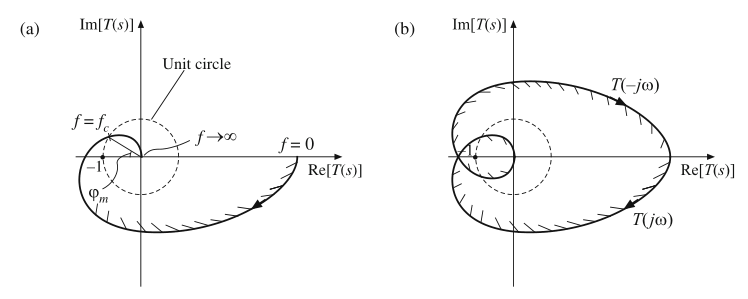
Fig. 9.16 Nyquist plot for an unstable system: (a) mapping of the contour \(Γ_A\) through the loop gain T(s), with negative phase margin \(\varphi_{m}\), (b) mapping of the complete Nyquist contour through the loop gain T(s)

示例2：三个穿越频率

作为第二个示例，让我们考虑在\(f=f_{1}\)处含有一个低频实极点，并且在超过第一个穿越频率的\(f=f_{2}\)处有高频谐振极点，那么其传递函数为：

\[T(s)=\cfrac{T_{0}}{(1+\cfrac{s}{\omega_{1}})(1+\cfrac{s}{Q\omega_{2}}+(\cfrac{s}{\omega_{2}})^2)} \tag{9.32} \]

在这种情况下的环路增益bode图如图9.17所示。在\(f_{2}\)处的谐振极点使得\(T\)的幅值在\(f_{2}\)处增加到0dB以上。因此，这里就有三个穿越频率(分别称为1,2,3)。这时的相位裕度可以说与每个穿越频率都有关系；对于图9.17所示的曲线，在穿越频率1和2的相位裕度是正的，而穿越频率3处的相位裕度是负的。因此，简单的相位裕度判断稳定性的方法这里又会造成歧义，这里有必要画出Nyquist曲线来判断这个环路增益是否使得系统是稳定的。

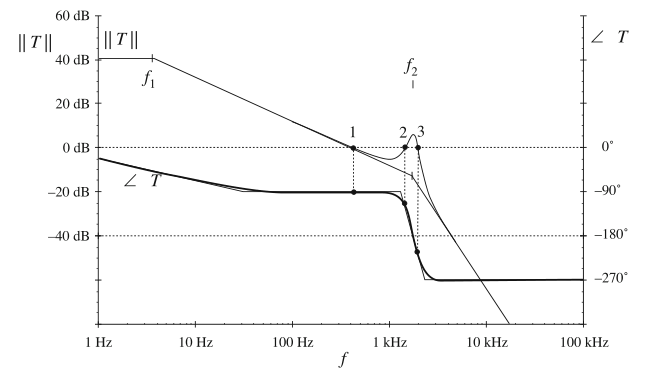
Fig. 9.17 Bode plot of loop gain T(s) for the example of Eq. (9.32). The loop gain exhibits three crossover frequencies

图9.18包含了与图9.17所示bode图对应的Nyquist图。图9.18a包含了映射曲线\(T(\Gamma_{A})=T(j\omega)\)，并标识了穿越点1,2,3。图9.18b给出了整个Nyquist曲线的映射。可以从中看出，(-1,0)点被包围了两次。因此，闭环传递函数在复平面的右半部分包含两个极点，并且该反馈系统是不稳定的。

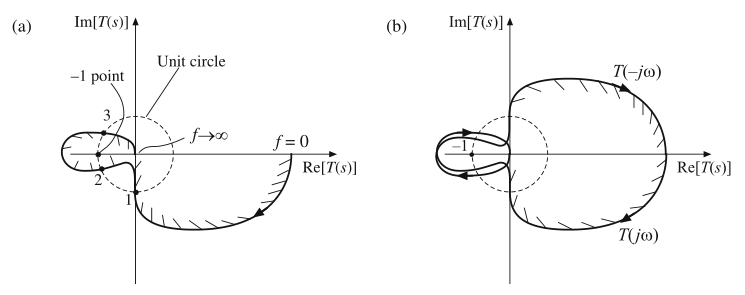
Fig. 9.18 Nyquist plot for the example having three crossover frequencies (Fig.9.17): (a) mapping of
the contour \(Γ_A\) through the loop gain T(s), (b) mapping of the complete Nyquist contour through the loop gain T(s)

示例3：反馈回路中的积分器

如果Nyquist曲线\(\Gamma\)通过环路增益的一个或多个奇点，那么保形映射的特性将不复存在，并且以上论点都不能适用了。当环路增益包含一个或多个位于虚轴上的极点时，就会发生这种情况。一个常见的例子是在补偿器中使用积分器(见9.5.2节)，导致原点存在一个极点。环路增益中包含原点为极点的一个例子为：

\[T(s)=\cfrac{1}{(\cfrac{s}{\omega_{0}})(1+\cfrac{s}{\omega_{1}})(1+\cfrac{s}{\omega_{2}})} \tag{9.33} \]

在这个例子中，转折频率\(\omega_{0},\omega_{1},\omega_{2}\)都是正实数。这种特殊情况，可以通过重新定义图9.13所示的Nyquist曲线，其具体方式如图9.19所示。添加了第4段曲线\(\Gamma_{D}\)，来绕过奇异点连接曲线。\(\Gamma_{D}\)的定义为半圆弧，如下所示：

\[s=\varepsilon e^{j\theta} \ \ with\ \ \varepsilon \rightarrow 0\ \ and\ \ \theta \in(-90°,90°) \tag{9.34} \]

式(9.33)的环路增益\(T(s)\)不包含位于如图9.19中修正后Nyquist曲线内部的极点。因此，闭环传递函数\(T/(1+T)\)的右半平面极点数等于映射的修改后Nyquist曲线\(T(\Gamma)\)对(-1,0)点的包围圈数。

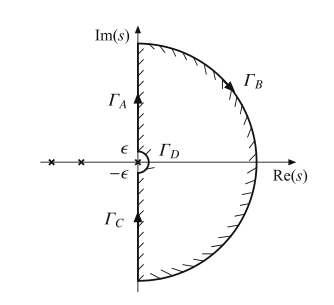
Fig. 9.19 Modification of the Nyquist contour to handle the special case in which the loop gain includes a pole at the origin. Segment \(Γ_D\) defined by Eq.(9.34) routes the Nyquist contour around the pole at s = 0. The locations of poles of Eq. (9.33) are marked ×

在给定的\(\omega_{0},\omega_{1},\omega_{2}\)的特定情况下，图9.20给出了\(T(s)\)的幅值和相角的bode图。在这个例子中，\(T(s)\)展示了一个穿越频率，其中标识了相位裕度\(\varphi_{m}\)。

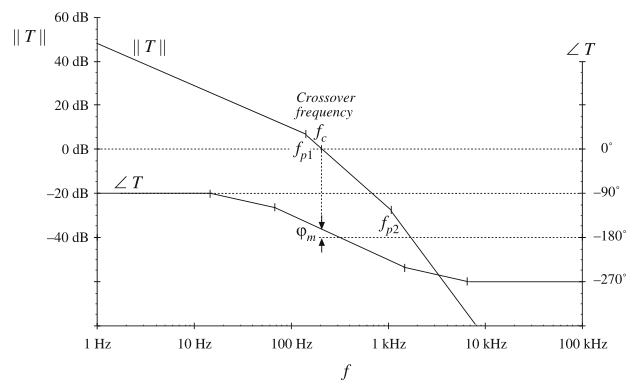
Fig. 9.20 Bode plot of loop gain T(s) for the example of Eq. (9.33)

图9.21a给出了Nyquist图的第一部分，其为\(\Gamma_{A}\)经环路增益\(T(s)\)映射得到。沿着这段，\(s=j\omega\)其中的\(\omega\)变化从\(\varepsilon(\rightarrow 0)\)到\(\infty\)。

\(\Gamma_{B}\)仍然由式(9.28)定义，这段仍然映射到原点。\(\Gamma_{C}\)是\(\Gamma_{A}\)的复共轭。曲线\(\Gamma_{A},\Gamma_{B},\Gamma_{C}\)通过环路增益\(T(s)\)的映射如图9.21b所示。可以看到这个曲线是不封闭的，\(\Gamma_{D}\)必须结合到这里。

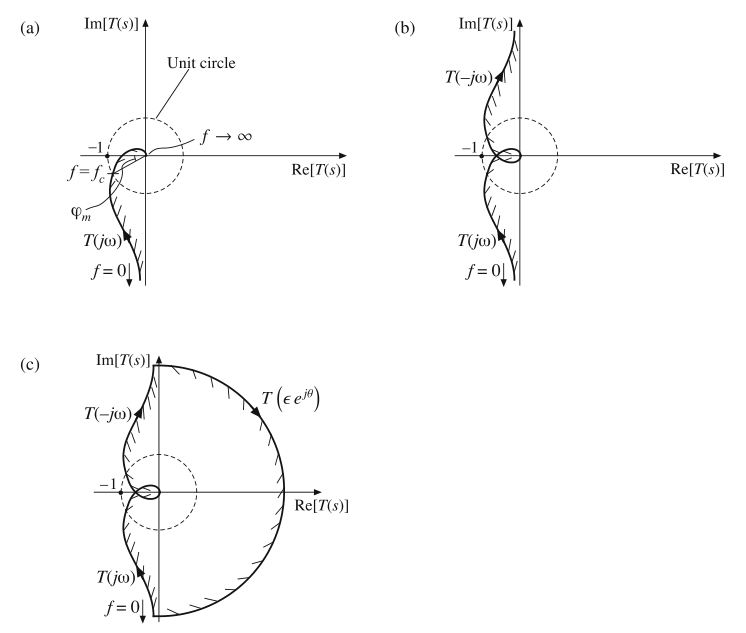
Fig. 9.21 Nyquist plot for the example of an integrator in the feedback loop (Fig.9.20): (a) mapping of the contour \(Γ_A\) through the loop gain T(s), (b) mapping of the contours \(Γ_A\), \(Γ_B\), and \(Γ_C\) through the loop gain T(s), (c) mapping of complete modified Nyquist contour

将(9.34)定义的映射代入式(9.33)的环路增益可以得到：

\[T(\varepsilon e^{j\theta})=\cfrac{1}{(\cfrac{\varepsilon e^{j\theta}}{\omega_{0}})(1+\cfrac{\varepsilon e^{j\theta}}{\omega_{1}})(1+\cfrac{\varepsilon e^{j\theta}}{\omega_{2}})} \tag{9.35} \]

当\(\varepsilon e^{j\theta} \rightarrow 0\)，与转折频率\(\omega_{1}\)和\(\omega_{2}\)对应的极点项趋向于1。式(9.35)简化为：

\[T(\varepsilon e^{j\theta})=\cfrac{\omega_{0}e^{-j\theta}}{\varepsilon} \tag{9.36} \]

当\(\varepsilon e^{j\theta} \rightarrow 0\)，式(9.36)的幅值趋向于无穷。当\(\theta\)从-90°变化到90°，映射曲线的相位从+90°变化到-90°。完整的曲线如图9.21c所示。可以看到，映射曲线是闭合的，并且没有对(-1,0)点进行包围，也就证明了相位裕度为正的。图9.21c表示了一个稳定的系统。

小结：Nyquist稳定判据

因此，Nyquist稳定判据与环路增益的bode图密切相关。\(\Gamma_{A}\)段对应的是令\(s=j\omega\)，并且\(\Gamma_{A}\)通过环路增益\(T(s)\)的映射构成了\(T(j\omega)\)的极坐标图。闭环传递函数\(T/(1+T)\)和\(1/(1+T)\)的右半平面极点数量可以通过对Nyquist曲线通过环路增益\(T(s)\)的映射后对(-1,0)包围的圈数来严格的确定。这也解释了相位裕度测试的来源，并且为更复杂的情况提供了稳定性分析方法(具有多个穿越频率的环路增益)。

9.4.3 相角裕度与闭环阻尼因子之间关系

我们需要多少相位裕量？最坏情况下相位裕度为1是否能够满足？当然，好的设计应具有足够的设计裕度，但是还有另一个重要原因需要额外的相位裕度。较小的相位裕度(在T中)使得闭环传递函数\(T/(1+T)\)和\(1/(1+T)\)在穿越频率附近表现出具有高\(Q\)值的谐振极点。系统的瞬态响应就表现出过冲和振铃。随着相角裕度的减小，这些特征将进一步恶化(高Q值，更长的振铃)，直到\(\varphi_{m}<0\)，系统变得不稳定。

让我们来考虑一个环路增益\(T(s)\)，它在穿越频率附近可以被以下函数很好的近似：

\[T(s)=\cfrac{1}{(\cfrac{s}{\omega_{0}})(1+\cfrac{s}{\omega_{2}})} \tag{9.37} \]

其幅值和相位渐近线如图9.22所示。对于那些在\(||T||\)中以-20dB每十倍频程接近单位增益，并且在\(f_{2}=\omega_{2}/2\pi\)处有一个额外极点的常见环路增益，在穿越频率处这个函数可以很好的近似。假定任何额外的零点和极点都足够高于或低于穿越频率，因此它们对穿越频率附近的系统传递函数的影响可忽略不计。

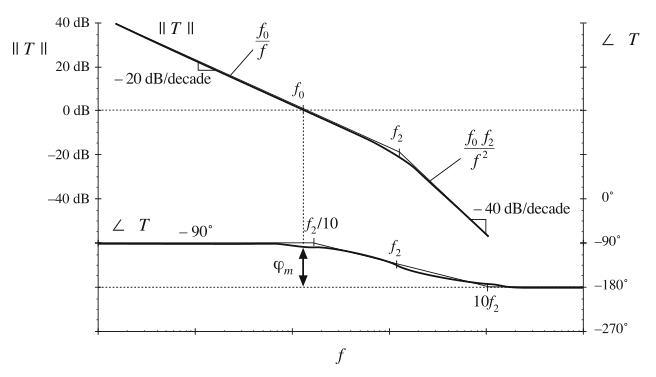
Fig. 9.22 Magnitude and phase asymptotes for the loop gain T of Eq. (9.37)

注意到，随着\(f_{2} \rightarrow \infty\)，相角裕度\(\varphi_{m}\)接近90°。随着\(f_{2} \rightarrow 0\)，\(\varphi_{m} \rightarrow 0°\)。因此，随着\(f_{2}\)的减小，相角裕度也减小了。让我们来研究这是如何通过\(T/(1+T)\)来影响闭环响应的。我们可以利用式(9.37)写出：

\[\cfrac{T(s)}{1+T(s)}=\cfrac{1}{1+\cfrac{1}{T(s)}}=\cfrac{1}{1+\cfrac{s}{\omega_{0}}+\cfrac{s^2}{\omega_{0}\omega_{2}}} \tag{9.38} \]

通过将其写为标准的一元二次形式，可以得到：

\[\cfrac{T(s)}{1+T(s)}=\cfrac{1}{1+\cfrac{s}{Q\omega_{c}}+(\cfrac{s}{\omega_{c}})^2} \tag{9.39} \]

其中：

\[\begin{aligned} & \omega_{c}=\sqrt{\omega_{0}\omega_{2}}=2\pi f_{c} \\ & Q=\cfrac{\omega_{0}}{\omega_{c}}=\sqrt{\cfrac{\omega_{0}}{\omega_{2}}} \end{aligned} \]

因此，闭环响应在\(f_{c}\)处包含二次极点，也就是\(f_{0}\)和\(f_{2}\)的几何平均值点。当\(f< < f_{2}\)时，这些极点具有低\(Q\)值系数。在这种情况下，我们可以使用低\(Q\)逼近来估计其频率：

\[\begin{aligned} & Q\omega_{0}=\omega_{0} \\ & \cfrac{\omega_{c}}{Q}=\omega_{2} \end{aligned} \tag{9.40} \]

这种情况下的幅值渐近线如图9.23所示。可以看到，这些渐近线符合9.3节中通过图形化代数方法构建\(T/(1+T)\)的规则。

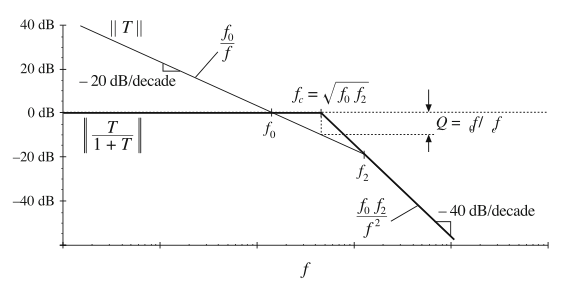
Fig. 9.23 Construction of magnitude asymptotes of the closed-loop transfer function T/(1 + T), for the low-Q case

接下来考虑高\(Q\)值的情况。当极点频率\(f_{2}\)减小，相角裕度也减小，由式(9.39)给出的\(Q\)系数增加。对于\(Q>0.5\)，谐振极点为\(f_{c}\)。图9.24给出了\(f_{2}< f_{0}\)情况下的幅值bode图。频率\(f_{c}\)仍然为\(f_{2}\)和\(f_{0}\)的几何平均值，并且\(f_{c}\)现在与\(||T||\)渐近线的穿越频率一致。闭环增益\(T/(1+T)\)在频率\(f_{c}\)处的实际值等于\(Q=f_{0}/f_{c}\)。如图9.24所示，这与频率\(f_{c}\)处的低频-20dB每十倍频程的渐近线\(f_{0}/f\)所得的值是相同的。可以看到，随着极点频率\(f_{2}\)的减小，\(Q\)系数变得很大。

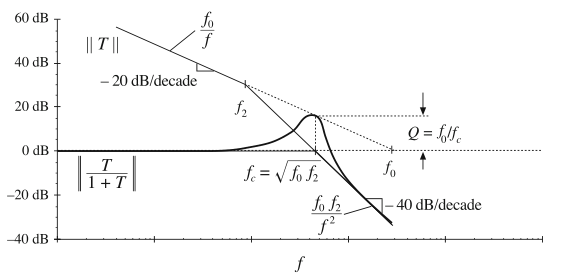
Fig. 9.24 Construction of magnitude asymptotes of the closed-loop transfer function T/(1 + T), for the high-Q case

图9.24的渐近线也遵循9.3节中的图形代数规则，单数通过曲线图上的代数方法无法预测精确曲线和渐近线之间的偏差。

这些具有\(Q\)系数的两个极点同时存在于\(T/(1+T)\)和\(1/(1+T)\)之中。我们需要找到一种简单的方法来确定\(Q\)系数。我们可以通过找到\(T\)的实际大小刚好等于1的频率来获得这样的关系。然后，我们可以通过评估该频率下的\(T\)的确切相位，并计算相角裕度。这个相位裕度是比值\(f_{0}/f_{2}\)或\(Q^{2}\)的函数。然后，我们求解出\(Q\)关于相角裕度的函数。其结果为：

\[\begin{aligned} & Q=\cfrac{\sqrt{cos \varphi_{m}}}{sin \varphi_{m}} \\ & \varphi_{m}=tan^{-1} \sqrt{\cfrac{1+\sqrt{1+4Q^4}}{2Q^4}} \end{aligned} \tag{9.41} \]

这个函数在图9.25中绘制，其中\(Q\)以dB表示。可以看出，要获得实极点\(Q< 0.5\)需要至少76°的相角裕度。为了获得\(Q=1\)，需要52°的相角裕度。相位裕度为1°时的系统表现出闭环响应的\(Q\)值非常高！在相位裕度很小的情况下，在穿越频率附近\(T(j\omega)\)非常接近1。其分母\((1+T)\)会变得非常小，使得闭环传递函数在接近穿越频率附近的频率处表现出峰值响应。

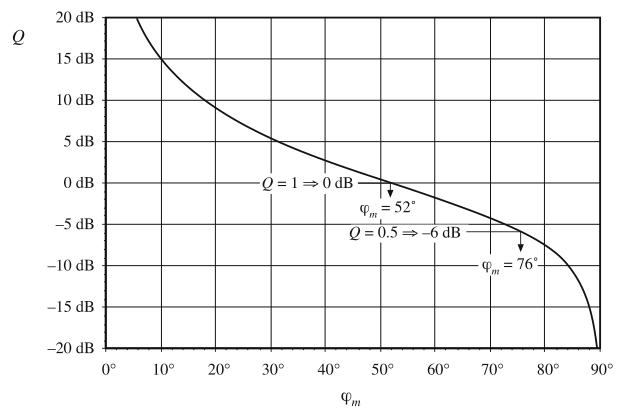
Fig. 9.25 Relationship between loop-gain phase margin \(\varphi_m\) and closed-loop peaking factor Q

图9.25就是式(9.37)定义的简单环路增益的结果。但这个环路增益对于那些实际中遇到的其他很多环路增益也能很好的近似，这些环路增益具有这样的特性：\(||T||\)以-20dB每十倍频程接近单位增益，并且在\(f_{2}\)处有一个额外的极点。如果\(T(s)\)的所有其他极点和零点都远高于或低于穿越频率，那么它们对穿越频率附近的系统传递函数的影响就可以忽略不计，并且图9.25给出了\(\varphi_{m}\)和\(Q\)之间的很好的近似关系。

另一个常见的情况是，\(||T||\)以-40dB每十倍频程斜率接近单位增益，并且在频率\(f_{2}\)处有一个额外的零点。随着\(f_{2}\)增加，相角裕度减小，\(Q\)增加。可以看到，\(\varphi_{m}\)与\(Q\)之间的关系与式(9.41)完全相同。

当环路增益\(T(s)\)包含三个或更多极点穿越频率附近的极点，图9.25就不能用了。闭环响应还包含接近三个或更多的极点，并且，这些极点不能完全由单个\(Q\)因子来表征。需要更多的工作才能找到确切的\(T/(1+T)\)和\(1/(1+T)\)在穿越频率附近的特性，但是无论如何可以说，较小的相位裕度会导致峰值闭环响应。

9.4.4 瞬态响应与阻尼因子

通过对式(9.39)乘以\(1/s\)并且通过Laplace逆变换，可以求解出\(T/(1+T)\)传递函数的单位阶跃响应。对\(Q>0.5\)的结果为：

\[\hat{v}(t)=1+\cfrac{2Qe^{-\omega_{c}t/2Q}}{\sqrt{4Q^2-1}}sin[\cfrac{\sqrt{4Q^2-1}}{2Q}\omega_{c}t+tan^{-1}(\sqrt{4Q^2-1})] \tag{9.42} \]

当\(Q<0.5\)时，结果为：

\[\hat{v}(t)=1-\cfrac{\omega_{2}}{\omega_{2}-\omega_{1}}e^{-\omega_{1}t}-\cfrac{\omega_{1}}{\omega_{1}-\omega_{2}}e^{-\omega_{2}t} \tag{9.43} \]

其中：

\[\omega_{1},\omega_{2}=\cfrac{\omega_{c}}{2Q}(1\pm \sqrt{1-4Q^2}) \tag{9.44} \]

图9.26给出了不同\(Q\)值的该方程曲线。

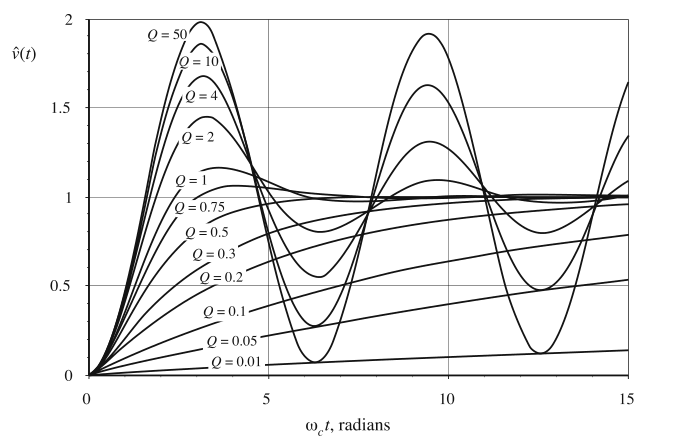
Fig. 9.26 Unit-step response of the second-order system, Eqs. (9.42) and (9.43), for various values of Q

根据式(9.39)，当\(f_{2}>4f_{0}\)，\(Q\)小于0.5，闭环响应包含一个低频和一个高频实极点。在这种情况下，瞬态响应为(9.43)，包含时间衰减指数，形式为：

\[Ae^{(pole)t} \tag{9.45} \]

这就被称为过阻尼的情况。当\(Q\)非常小时，低频极点会使得阶跃响应变得非常慢。

当\(f_{2}=4f_{0}\)，\(Q\)系数等于0.5。闭环响应在\(2f_{0}\)处包含两个实极点。这被称为临界阻尼情况。其瞬态响应比过阻尼情况更快，因为其最低频率极点处于较高的频率处。这是不会表现出过冲的最快的响应。在弧度\(\omega_{c}t= \pi\)，(\(t=1/2f_{c}\))时，电压已经达到其终值的82%。在弧度\(\omega_{c}t= 2\pi\)，(\(t=1/f_{c}\))时，电压已经达到其终值的98.6%。

当\(f_{2}< 4f_{0}\)，\(Q\)大于0.5。闭环响应包含复数极点，瞬态响应表现为正弦型波形，并且其幅值在衰减，见式(9.42)。阶跃响应的上升时间比临界阻尼情况要快，但波形会出现过冲现象。\(v(t)\)的峰值为：

\[peak\ \hat{v}(t)=1+e^{-\pi/\sqrt{4Q^2-1}} \tag{9.46} \]

这被称为欠阻尼。\(Q\)系数为1会导致16.3%的超调，而\(Q\)为2时会导致44.4%的超调。更大的\(Q\)系数可能导致过冲超过100%。

由于\(T\)中的附加极点和零点以及初始条件的不同，反馈回路的实际瞬态响应可能与图9.26所示并不相同。尽管如此，图9.26仍然说明了高\(Q\)值的极点如何导致过冲和振铃。例如，在3.3V的计算机供电系统中，打开电源，不能使电压过冲至5或者6V--这可能损坏计算机中的集成电路。因此，\(Q\)系数必须足够小，通常为0.5甚至更小，对应于至少76°的相角裕度。

9.4.5 负载阶跃响应与阻尼系数

通常，我们对输出电压对负载电流阶跃变化的响应也比较感兴趣。让我们来考虑这个情况，闭环输出阻抗可以通过以下形式的二阶函数很好的近似：

\[Z_{out}(s)=\cfrac{(\cfrac{sR_{0}}{\omega_{c}})}{1+\cfrac{s}{Q\omega_{c}}+(\cfrac{s}{\omega_{c}})^2} \tag{9.47} \]

这就构成了具有特征阻抗\(R_{0}\)，谐振频率\(f_{c}\)以及\(Q\)系数为\(Q\)的等效并联\(R-L-C\)阻抗。同样考虑到负载电流采用以下拉普拉斯变换的幅值为\(I_{0}\)的阶跃变化：

\[\hat{i}_{load}=\cfrac{I_{0}}{s} \tag{9.48} \]

可以将其乘以式(9.47)和(9.48)，然后通过拉普拉斯逆变换来推导输出电压响应表达式\(\hat{v}(t)\)。对于\(Q<0.5\)，其结果为：

\[\hat{v}(t)=-\cfrac{I_{0}R_{0}Q}{\sqrt{1-4Q^2}}(e^{-\omega_{1}t}-e^{-\omega_{2}t}) \tag{9.49} \]

其中\(\omega_{1},\omega_{2}\)在式(9.44)中定义了。对于高\(Q\)值情况，\(Q>0.5\)，结果为：

\[\hat{v}(t)=-\cfrac{I_{0}R_{0}Q}{\sqrt{1-4Q^2}} e^{\omega_{c}t/2Q} sin(\cfrac{\sqrt{4Q^2-1}}{2Q} \omega_{c}t) \tag{9.50} \]

在\(I_{0}R_{0}=1\)和不同的\(Q\)值情况下的上述方程的值在图9.27中描绘了出来。对于不等于1时的\(I_{0}R_{0}\)可以通过将曲线乘以该值即可：\(\hat{v}(t)\)的峰值之间的偏差值正比于电流阶跃\(I_{0}\)乘以特征阻抗\(R_{0}\)。在\(Q<0.5\)时，峰值电压偏差值略小于\(I_{0}R_{0}Q\)。\(Q=0.5\)时，峰值电压偏差值近似为\(-0.368I_{0}R_{0}\)。当\(Q \rightarrow \infty\)时，峰值电压偏差值为\(-I_{0}R_{0}\)。

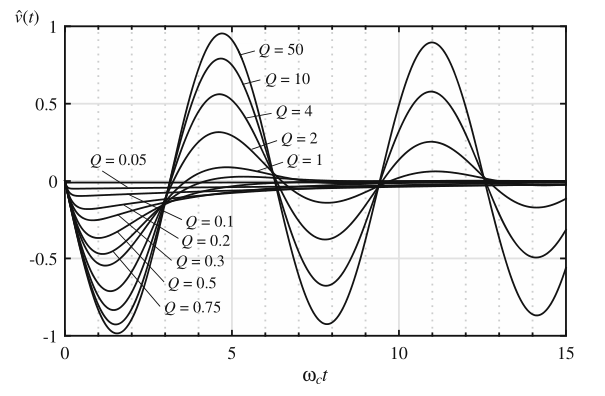
Fig. 9.27 Response of the second-order system to a unit step change in load current, Eqs. (9.49)
and (9.50), for various values of Q. These curves are plotted for \(I_0R_0\)= 1