[Fundamental of Power Electronics]-PART II-9. 控制器设计-9.2 负反馈对网络传递函数的影响

9.2 负反馈对网络传递函数的影响

我们已经知道了如何推导开关变换器的交流小信号传递函数。例如，buck变换器的等效电路模型可以表示为图9.3所示。这个等效电路包含三个独立输入：控制输入变量\(\hat{d}\)，输入电压变量\(\hat{v}_{g}\)，以及负载电流变量\(\hat{i}_{load}\)。那么输出电压变量\(\hat{v}\)可以表示为上述三个变量的线性组合，也就是：

\[\hat{v}(s)=G_{vd}(s)\hat{d}(s)+G_{vg}(s)\hat{v}_{g}(s)-Z_{out}\hat{i}_{load}(s) \tag{9.1} \]

其中：

\[\begin{aligned} & G_{vd}(s)=\cfrac{\hat{v}(s)}{\hat{d}(s)}|_{\hat{v}_{g}=0,\hat{i}_{load}=0} \\ & G_{vg}(s)=\cfrac{\hat{v}(s)}{\hat{v}_{g}(s)} |_{\hat{d}=0,\hat{i}_{load}=0} \\ & Z_{out}(s)=-\cfrac{\hat{v}(s)}{\hat{i}_{load}(s)} |_{\hat{d}=0,\hat{v}_{g}=0} \end{aligned} \]

第八章构建了这些量的bode图。式(9.1)描述了\(v_{g}\)和\(i_{load}\)的扰动是如何通过传递函数\(G_{vg}(s)\)和输出阻抗\(Z_{out}(s)\)影响输出电压\(v\)的。如果已知扰动\(v_{g}\)和\(i_{load}\)的最坏情况下的最大幅值，那么式(9.1)可以用来计算最坏情况下的\(v\)的开环变化。

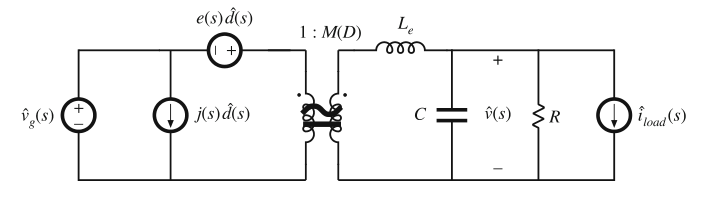
Fig. 9.3 Small-signal converter model, which represents variations in \(v_g\), \(d\), and \(i_{load}\)

如前所述，图9.2的反馈环路可以用来减小\(v_{g}\)和\(i_{load}\)对输出电压\(v\)的影响。为了分析这个系统，我们对有关其静态工作点的平均信号进行扰动和线性化。功率级和控制部分均收到扰动和线性化：

\[\begin{aligned} & v_{ref}(t)=V_{ref}+\hat{v}_{ref}(t) \\ & v_{e}(t)=V_{e}+\hat{v}_{e}(t)\\ & etc. \end{aligned} \tag{9.2} \]

在直流稳压器系统中，参考输入是定值，因此\(\hat{v}_{ref}=0\)。在开关放大器或逆变器中，参考输入可能包含交流变化量。在图9.4a中，图9.3中的变换器模型与扰动和线性化及控制相结合。通过将变换器模型用式(9.1)替换，这个等效电路可以简化为图9.4b所示的框图。

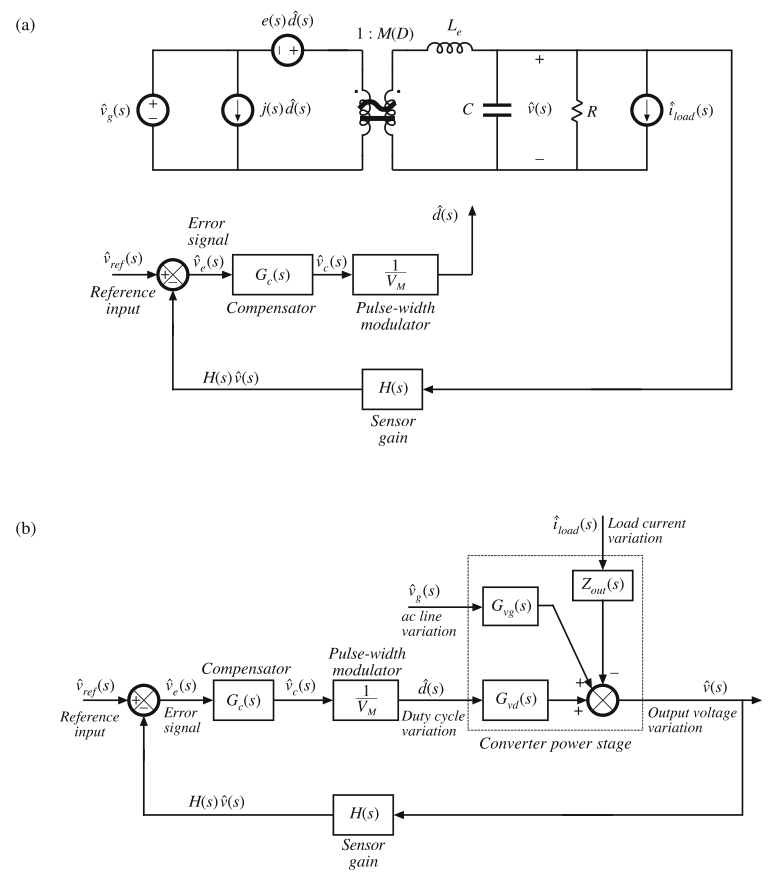
Fig. 9.4 Voltage regulator system small-signal model: (a) with converter equivalent circuit; (b) complete
block diagram

图9.4b中输出电压变化量\(\hat{v}\)的解为：

\[\hat{v}=\hat{v}_{ref}\cfrac{G_{c}G_{vd}/V_{M}}{1+HG_{c}G_{vd}/V_{M}}+\hat{v}_{g} \cfrac{G_{vg}}{1+HG_{c}G_{vd}/V_{M}}-\hat{i}_{load} \cfrac{Z_{out}}{1+HG_{c}G_{vd}/V_{M}} \tag{9.3} \]

也可以写为以下形式：

\[\hat{v}=\hat{v}_{ref} \cfrac{1}{H} \cfrac{T}{1+T}+\hat{v}_{g} \cfrac{G_{vg}}{1+T}-\hat{i}_{load} \cfrac{Z_{out}}{1+T} \tag{9.4} \]

其中：

\[T(s)=H(s)G_{c}(s)G_{vd}(s)/V_{M}="loop\ gain" \]

式(9.4)是一个通用结果。环路增益\(T(s)\)被定义为环路的前向通道与反馈通道增益乘积。这个方程显示了添加反馈回路如何改变系统的传递函数和性能，具体的内容将在下面介绍。

9.2.1 反馈减小扰动到输出的传递函数

图9.3所示的开环buck变换器的\(v_g\)到\(v\)的传递函数\(G_{vg}(s)\)由式(9.1)给出。当反馈被添加时，根据式(9.4)传递函数变为：

\[\cfrac{\hat{v}(s)}{\hat{v}_{g}(s)}|_{\hat{v}_{ref}=0,\hat{i}_{load}=0}=\cfrac{G_{vg}(s)}{1+T(s)} \tag{9.5} \]

因此，通过反馈，该传递函数变小了\(1/(1+T(s))\)。如果环路增益\(T(s)\)的幅值较大，那么减小的幅度也会很大。因此，由给定电压\(v_{g}\)的变化量造成的输出电压变化被反馈环路给衰减了。

式(9.4)同样可以证明变换器输出阻抗被减小了， 从\(Z_{out}(s)\)到：

\[\cfrac{\hat{v}(s)}{-\hat{i}_{load}(s)}|_{\hat{v}_{g}=0,\hat{v}_{ref}=0}=\cfrac{Z_{out}(s)}{1+T(s)} \tag{9.6} \]

因此，反馈环路还将变换器的输出阻抗减小了\(1/(1+T(s))\)，并且减小了负载电流变化对输出电压的影响。

9.2.2 反馈使得从参考输入到输出的传递函数对环路前向通道增益变化不敏感

根据式(9.4)，从\(v_{ref}\)到\(v\)的闭环传递函数为：

\[\cfrac{\hat{v}(s)}{\hat{v}_{ref}(s)}|_{\hat{v}_{g}=0,\hat{i}_{load}=0}=\cfrac{1}{H(s)} \cfrac{T(s)}{1+T(s)} \tag{9.7} \]

如果环路增益的幅值非常大，也就是\(||T||>>1\)，那么\((1+T) \approx T\)并且\(T/(1+T)\approx T/T=1\)。传递函数变为：

\[\cfrac{\hat{v}(s)}{\hat{v}_{ref}(s)} \approx \cfrac{1}{H(s)} \tag{9.8} \]

其与\(G_{c}(s)\)，\(V_{M}\)和\(G_{vd}(s)\)都无关。因此，假设环路增益的幅值较大，那么\(G_{c}(s)\)，\(V_{M}\)和\(G_{vd}(s)\)的变化对输出电压的影响可以忽略不计。当然，在直流稳压器应用中，\(v_{ref}(t)\)是常数并且\(\hat{v}_{ref}=0\)。这里式(9.8)同样适用，于直流量。例如，如果系统是线性的，我们可以写为：

\[\cfrac{V}{V_{ref}}=\cfrac{1}{H(0)} \cfrac{T(0)}{1+T(0)} \approx \cfrac{1}{H(0)} \tag{9.9} \]

因此，要使直流输出电压\(V\)准确跟随直流参考电压\(V_{ref}\)，我们只需要保证直流反馈增益\(H(0)\)和参考电压\(V_{ref}\)是精确的，并且\(T(0)\)足够大。通常使用精密电阻来构造\(H\)，但在\(G_{c}\)，脉冲宽度调制器以及功率级无需使用具有严格控制值的器件。输出电压对前向通道中增益的灵敏度降低，而\(v\)对反馈增益\(H\)和参考输入\(v_{ref}\)的灵敏度上升。