[Fundamental of Power Electronics]-PART II-9. 控制器设计-9.1 引言
9.1 引言
在所有的开关变换器中,输出电压\(v(t)\)都是输入电压\(v_{g}(t)\),占空比\(d(t)\),负载电流\(i_{load}(t)\)和电路元件值的函数。在DC-DC变换器应用场合,尽管\(v_{g}(t)\)和\(i_{load}(t)\)可能会有扰动,并且电路元件值可能变化,但仍然希望获得一个恒定的输出电压\(v(t)=V\)。这些扰动的来源可能有很多,一个典型的电路如图9.1所示。由off-line power supply(译者:离线电源供电,有说法解释为整流和滤波前无工频变压器)的输入电压\(v_{g}(t)\)通常包含由整流器产生的交流电源系统频率的二次谐波(100Hz或者120Hz)。当相邻的电力设备开关时,\(v_{g}(t)\)的幅值也可能会变化。负载电流\(i_{load}(t)\)也可能包含较大幅度的变化,并且典型的电源规格为:当负载电流阶跃变化时(比如电流从50%变化到额定值),输出电压必须保持在指定范围内(例如:3.3V±0.05V),反之亦然。电路元件的值在制造时通常具有一定的公差,因此在大批量制造某种变换器时,变换器的输出电压处于某种分布。我们期望所有这种分布都处在规定范围之内。但是,如果不使用负反馈,这些都是不切实际的。除了输出电压是交流的之外,逆变器也应该考虑这些类似的问题。
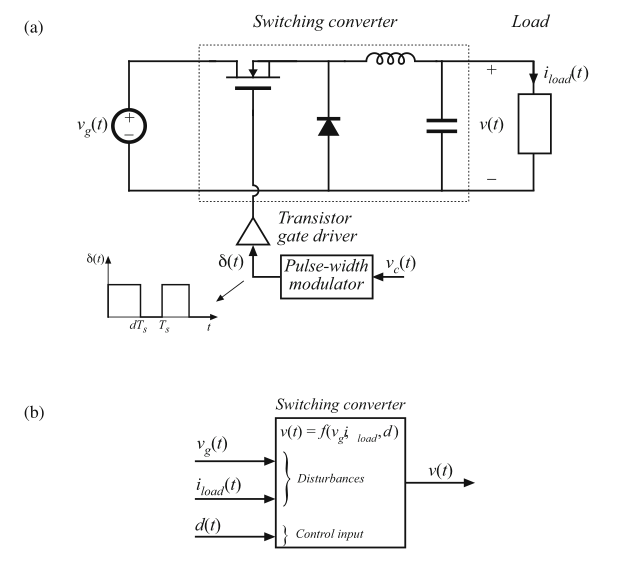
Fig. 9.1 The output voltage of a typical switching converter is a function of the line input voltage \(v_g\), the duty cycle \(d\), and the load current \(i_{load}\): (a) open-loop buck converter; (b) functional diagram illustrating dependence of \(v\) on the independent quantities \(v_g\), \(d\), and \(i_{load}\)
因此,我们不能期望简单地将DC-DC变换器占空比设置为单个值而能在所有的条件下都获得给定的恒定输出电压。使用负反馈背后的思想是构建一个电路,这个电路可根据需要自动调整占空比,从而获得高精度的输出电压,而与\(v_{g}(t)\)或者\(i_{load}(t)\)的干扰或者元件值变化无关。每当存在变化和未知因素可能导致系统输出不能获得所需的性能时,这是非常有用的。
图9.2给出了一个反馈系统的框图。使用增益为\(H(s)\)的传感器可以测量输出电压\(v(t)\)。在直流稳压器或直流-交流逆变器中,传感器电路通常为精密电阻组成的分压器。将传感器输出信号\(H(s)v(s)\)与输入参考电压\(v_{ref}(s)\)进行比较。目标是令\(H(s)v(s)\)等于\(v_{ref}(s)\),从而使\(v(s)\)精确跟踪\(v_{ref}(s)\),而不用考虑补偿器,脉冲宽度调制器,以及门极驱动和变换器功率级的变化。
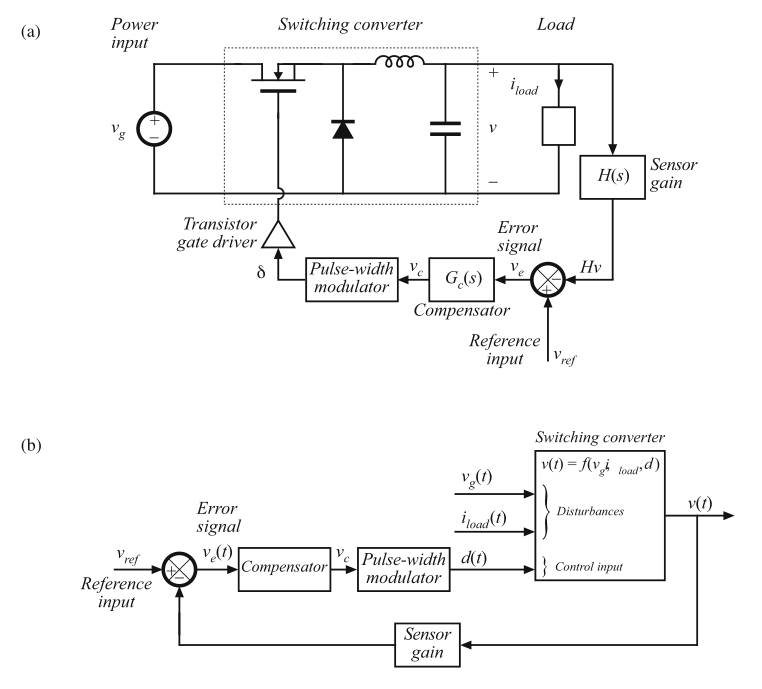
Fig. 9.2 Feedback loop for regulation of the output voltage: (a) buck converter, with feedback loop block diagram; (b) functional block diagram of the feedback system
参考输入\(v_{ref}(s)\)与传感器输出\(H(s)v(s)\)之间的差值被称为误差信号\(v_{e}(s)\)。如果反馈系统完美工作,那么\(v_{ref}(s)=H(s)v(s)\),因此误差信号为0。实际上,这个误差信号通常不等于0,但是也是非常小的一个值。如图9.2所示,获得一个小误差就是添加补偿网络\(G_{c}(s)\)的目标之一。注意,从误差信号\(v_{e}(s)\)到输出电压\(v(s)\)的传递函数等于补偿器,脉冲宽度调制器以及功率级的增益。如果补偿器\(G_{c}(s)\)在幅值上足够大,那么一个很小的误差信号就可以为直流稳压器产生所需的输出电压\(v(t)=V\)。(Q:如何选择\(H\)和\(v_{ref}\))。因此,较大的补偿器增益就使得误差信号较小,也就是输出跟随参考输入的精度很高。这就是反馈系统背后的关键思想。
第七章中推导出的平均小信号变换器模型将在后面用来得到反馈对稳压器小信号传递函数的影响。环路增益\(T(s)\)定义为反馈回路中前向通道和反馈通道中小信号增益的乘积。我们还可以看到,从扰动到输出的传递函数 就是对其乘以系数\(1/(1+T_{s})\)。因此我们可以看到,当环路增益\(T\)的幅值越大,干扰对输出电压的影响就越小。较大的环路增益还会导致输出电压\(v(s)\)几乎等于\(v_{ref}(s)/H(s)\),而对于反馈环路的前向路径中增益的依赖较小。因此,环路增益的幅值\(||T||\)是衡量反馈系统运行情况的一个指标。使用图形化的代数方法可以轻松构建这些增益。这样就可以很轻松的评估重要的闭环性能指标,由输入整流器造成的\(v_{g}(t)\)中的120Hz纹波和闭环输出阻抗产生的输出电压纹波。
稳定性是反馈系统中的另一个重要问题。对稳定性的深入研究超出了本书的范围。但是,这里使用了用于评估稳定性的简单相位裕度标准。当环路增益\(T\)的相位裕度为正时,反馈系统稳定。此外,增加相位裕度可以使系统的瞬态响应变得更好,并且具有较小的过冲和振荡。9.4节中对相位裕度与闭环响应的关系进行了量化。
9.5节中给出了一个为直流稳压器系统设计补偿网络的例子。补偿器网络旨在获得足够的相位裕度以及对预期干扰的良好抑制。超前补偿器和PD控制器可用于改善相位裕度并拓展反馈环路的带宽。这样可以更好地抑制高频干扰。滞后补偿器和PI控制器可以用于增加低频环路增益。这样可以更好地抑制低频干扰和非常小的稳态误差。更加复杂的补偿器可以实现两种方法都具有的优点。
9.6节介绍了用于环路增益实验测量的注入方法。电压或电流注入的使用解决了在高增益系统中建立合适静态工作点的问题。得到了获得精确测量的条件。注入方法还可以测量不稳定系统的环路增益。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号