[Fundamental of Power Electronics]-PART II-8. 变换器传递函数-8.1 Bode图回顾

8.0 序

工程设计过程主要包括以下几个过程：

1.定义规格与其他设计目标

2.提出一个电路。这是一个创造性的过程，需要利用工程师的实际见识和经验。

3.对电路进行建模。变换器的功率级建模方法已经在第7章给出。系统各元件和其他部分通常使用供应商提供的数据进行建模。

4.对电路进行面向设计的分析。这就涉及到了方程的建立，这些方程可以通过选择不同的元素值从而满足设计规格和设计目标。此外，工程师有必要对电路特性有更多的了解和物理角度的见解，从而可以通过向电路中添加元件或更改电路的连接改进设计。

5.模型验证。在常规条件下，将模型与实验室原型产品进行比较。可以根据需要对模型进行改进，从而使得模型预测的结果与实验室测量结果保持一致。

6.进行电路最恶劣条件分析(或其他可靠性分析和成品率分析)。这就涉及到了模型性能的定量评估，判断是否在所有条件下都满足设计要求。计算机仿真非常适合做这个分析。

7.迭代。重复上述步骤来改进设计，直到最坏情况下的特性都满足规范，或直到可靠性或者良品率都达到可接受的高水平为止。

本章涵盖了步骤4,5和6中需要的面向设计的分析技术，实验传递函数测量和计算机仿真。

第8.1到8.3节讨论了分析和构建变换器传递函数，输入阻抗和输出阻抗的波特图技术，并且这里的方程都由第7章的等效电路模型得到。比如说，buck-boost变换器的小信号等效电路模型如图7.18c所示。这个模型如图8.1所示，其中标识了非常重要的输入和输出端口阻抗。通过将占空比变化量\(\hat{d}(s)\)设置为0，求解从\(\hat{v}_{g}(s)\)到\(\hat{v}(s)\)的传递函数就得到了输入输出传递函数\(G_{vg}(s)\)：

\[G_{vg}(s)=\cfrac{\hat{v}(s)}{\hat{v_{g}}(s)}|_{\hat{d}(s)=0} \tag{8.1} \]

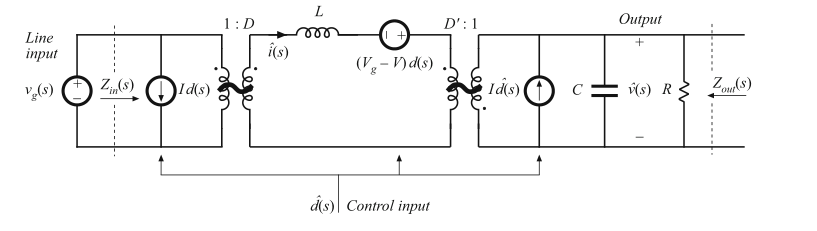
Fig. 8.1 Small-signal equivalent circuit model of the buck–boost converter, as derived in Chap. 7

这个传递函数描述了输入电压\(v_{g}(t)\)的变化或者扰动是如何导致输出电压\(v(t)\)的扰动的。在设计输出电压控制器时，这一点是非常重要的。例如，在一个off-line(译者：非交流直接供电，需要转换，含义模糊)供电系统中，变换器的输入电压\(v_{g}(t)\)包含不期望的交流电源电压的偶次谐波。\(G_{vg}(s)\)就可以用来研究这些谐波对变换器输出电压\(v(t)\)的影响。

控制到输出的传递函数\(G_{vd}(s)\)是通过将输入电压的变化量\(\hat{v}_{g}(s)\)设置为0，从而求解\(\hat{v}(s)\)关于\(\hat{d}(s)\)的函数关系：

\[G_{vd}(s)= \cfrac{\hat{v}(s)}{\hat{d}(s)}|_{\hat{v}_{g}(s)=0 } \tag{8.2} \]

这个传递函数描述了控制输入的变化量\(\hat{d}(s)\)是如何影响输出电压\(\hat{v}(s)\)的。在一个输出电压控制系统中，\(G_{vd}(s)\)是环路增益的重要组成部分，对调节器的性能有重要影响。

在\(\hat{v}_{g}(s)\)和\(\hat{d}(s)\)都被设为0时，就可以求出输出阻抗\(Z_{out}(s)\)。输出阻抗\(Z_{out}(s)\)描述了负载电流的变化是如何影响输出电压的。这个量对于输出电压控制器的设计也是非常重要的。并且在定义\(Z_{out}(s)\)时，是否包含负载电阻应视情况而定。

当在变换器的电源输入端口添加EMI滤波器时，变换器的输入阻抗就变得非常重要。\(Z_{in}\)和EMI滤波器的输出阻抗幅值相对大小影响着EMI滤波器是否会干扰传递函数\(G_{vd}(s)\)。EMI滤波器的设计是第17章的主要内容。

本章的目的是构建传递函数和开关变换器端口阻抗的波特图。例如，图8.2给出了图8.1所示buck-boost变换器模型的\(G_{vd}(s)\)的幅值和相角图。幅值和相位渐进线的构建方法在8.1节中进行了回顾，其中包括了两种常在变换器传递函数中出现的特征：谐振和右半平面零点。buck-boost变换器的小信号传递函数的bode图构建在8.2节中进行了详细的描述，并且基本的buck，boost以及buck-boost变换器的传递函数都以表格形式列出。还对右半平面物理原理进行了描述。

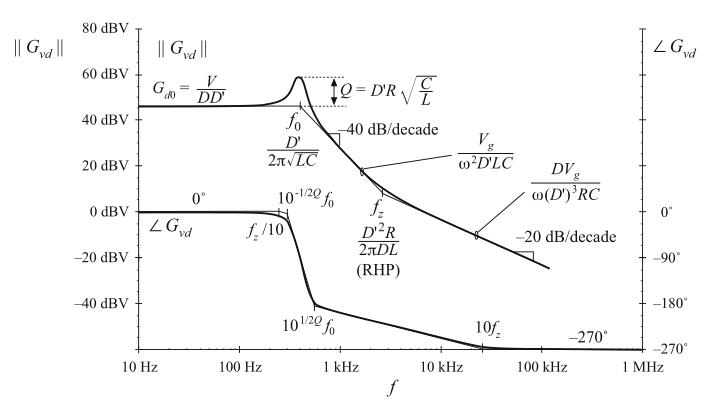
Fig. 8.2 Bode plot of control-to-output transfer function predicted by the model of Fig.8.1, with analytical expressions for the important features

电路分析(步骤中的第4步)中通常遇到的困难是模型的复杂性：实际电路中可能包含数百个元件，因此对其分析可能会导致复杂的推导，棘手的方程式以及可能出现大量的代数错误。面向设计的分析是可以减轻这些问题的工具和技术的合集。本章介绍了一些用于设计复杂变换器系统的工具。以规范化的形式编写传递函数可直接暴露响应的重要特征。这些特征和渐近线的解析表达式产生了在设计中有用的简化方程式。传递函数多项式的分离根是很简单的。8.3节给出了一种构建传递函数和阻抗bode图的图形化方法，其本质是观察法。这种方法可以：(1) 减小代数和相关的代数错误； (2) 对电路特性可以有更深入的理解，可用于设计电路；(3) 得到重要观察结果以作出合适的近似来使方程更加容易求解。第四部分介绍了一些更高级的面向设计的分析方法。

传递函数和阻抗的实验测量(第4步，模型验证中需要)在第8.5节中进行了讨论。在第14章中介绍了使用计算机仿真来绘制传递函数bode图。(第6步的最恶劣情况分析)

8.1 Bode图回顾

Bode图就是传递函数或者其他复数量的幅值和相角关于频率的图。使用半对数坐标轴绘制了以分贝为单位的幅值和度为单位的相位与频率的关系。幅值图实际上是对数-对数坐标图，因为幅值以分贝表示，而频率轴是对数。

无量纲值\(G\)的大小可以用分贝表示如下：

\[||G||_{dB}=20log_{10}(||G||) \tag{8.3} \]

表8.1列出了一些常见幅值的分贝值。必须要注意的是，要使用无量纲的值。因为获取有量纲数的对数是不合适的，所以必须将大小标幺化。例如，为了表示以分贝为单位的阻抗\(Z\)的大小，我们应该除以基准阻抗\(R_{base}\)来归一化：

\[||Z||_{dB}=20log_{10}(\cfrac{||Z||}{R_{base}}) \tag{8.4} \]

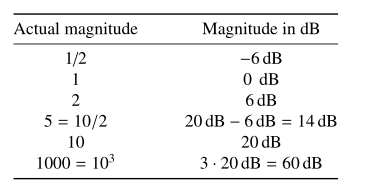
Table 8.1 Expressing magnitudes in decibels

\(R_{base}\)的选取是任意的，但我们必须告诉别人我们选择的是哪个值。所以，如果\(||Z||\)是\(5\ \Omega\)，我们选择的\(R_{base}\)是\(10\ \Omega\)，那么我们就可以说，相对于\(10\ \Omega\)，\(||Z||_{dB}=20log_{10}(5\Omega/10\Omega)=-6\ dB\)。常用的选择是\(R_{base}=1\Omega\)，用\(R_{base}=1 \ \Omega\)表示的分贝阻抗常被称为\(dB\Omega\)。因此，\(5 \ \Omega\)等效于\(14dB \Omega\)。变换器输入端口的电流开关纹波，通常以\(dB\mu A\)表示，或使用\(1 \ \mu A\)的电流基准以\(dB\)表示：\(60dB \mu A\)等效于\(1000 \ \mu A\)或者\(1\ mA\)。

幅值等于\(f\)的幂函数的Bode图的是线性的。例如，假设无量纲值\(G(f)\)的幅值大小为：

\[||G||=(\cfrac{f}{f_{0}})^{n} \tag{8.5} \]

其中\(f_{0}\)和\(n\)为常数。将幅值以对数形式表述为：

\[||G||_{dB}=20log_{10}(\cfrac{f}{f_{0}})^{n}=20nlog_{10}(\cfrac{f}{f_{0}}) \tag{8.6} \]

图8.3给出了以不同\(n\)值绘制出的该方程的曲线。频率在\(f=f_{0}\)处，幅值为1也就是\(0\ dB\)。他们是\(log_{10}(f)\)的函数。\(log_{10}(f)\)单位变化引起的\(||G||_{dB}\)的变化就是其斜率：\(log_{10}(f)\)的单位增加对应于\(f\)的10倍增加。从式(8.6)中，\(f\)的十倍频程增加使得\(||G||_{dB}\)增加了\(20n\ dB\)。因此，这里的斜率就是\(20n \ dB\)每十倍频程。等效的，我们也可以说斜率为\(20n\ log_{10}(2)\approx 6n\ dB\)倍频程(per octave)，其中倍频程(per octave)指的是频率以系数2增加。实际中，大多数频率相关函数的幅值通常可以在有限的频率范围内通过式(8.5)所示的函数来近似；在这个频率范围内，bode图幅值的大小近似与\(20n\ dB/decade\)(\(20n \ dB\)每十倍频程)。

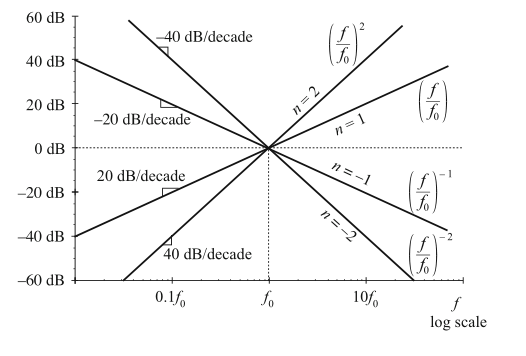
Fig. 8.3 Magnitude Bode plots of functions which vary as \(f_{n}\) are linear, with slope \(n\ dB\) per decade

一个形如式(8.5)所示的简单传递函数，其极点为原点：

\[G(s)=\cfrac{1}{(\cfrac{s}{\omega_{0}})} \tag{8.7} \]

其幅值为：

\[||G(j\omega)||=\cfrac{1}{||\cfrac{j\omega}{\omega_{0}}||}=\cfrac{1}{(\cfrac{\omega}{\omega_{0}})} \tag{8.8} \]

如果定义\(f=\omega/2\pi\)以及\(f_{0}=\omega_{0}/2\pi\)，式(8.8)变为：

\[||G||=(\cfrac{f}{f_{0}})^{-1} \tag{8.9} \]

这就是式(8.5)中\(n=-1\)的情况。如图8.3所示，原式为(8.7)的极点为原点的式子的bode图幅值斜率为\(-20 \ dB\)每十倍频程，并且在\(f=f_{0}\)时穿过\(0\ dB\)。

8.1.1 单极点响应

考虑图8.4所示的简单低通RC滤波器。传递函数由分压比得到：

\[G(s)=\cfrac{v_{2}(s)}{v_{1}(s)}=\cfrac{\cfrac{1}{sC}}{\cfrac{1}{sC}+R} \tag{8.10} \]

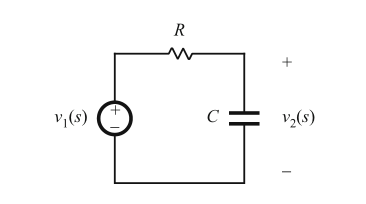
Fig. 8.4 Simple R–C low-pass filter example

这个传递函数是电压的比值，所以其是无量纲的。将分子与分母乘以\(sC\)，可以将传递函数表示为有理分数：

\[G(s)=\cfrac{1}{1+sRC} \tag{8.11} \]

现在将传递函数与以下针对单极标准归一化形式一致：

\[G(s)=\cfrac{1}{(1+\cfrac{s}{\omega_{0}})} \tag{8.12} \]

参数\(\omega_{0}=2\pi f_{0}\)，令式(8.11)和(8.12)中的\(s\)的系数相等，结果为：

\[\omega_{0}= \cfrac{1}{RC} \tag{8.13} \]

由于\(R\)和\(C\)是正实数，\(\omega_{0}\)也是正实数。式(8.12)的根为\(s=-\omega_{0}\)，因此，\(G(s)\)在复平面的左半平面有一个实极点。

为了求解传递函数的幅值和相角，我们让\(s=j\omega\)，其中\(j\)是-1的平方根。然后我们就可以得到复数函数的幅值大小和相位。当\(s=j\omega\)时，式(8.12)变为：

\[G(j\omega)=\cfrac{1}{(1+j\cfrac{\omega}{\omega_{0}})}=\frac{1-j\cfrac{\omega}{\omega_{0}}}{1+(\cfrac{\omega}{\omega_{0}})^{2}} \tag{8.14} \]

对于某个特定的\(\omega\)值，复数\(G(j\omega)\)如图8.5所示。其幅值为：

\[||G(j\omega)||=\sqrt{[Re(G(j\omega))]^2+[Im(G(j\omega))]^2}=\cfrac{1}{\sqrt{1+(\cfrac{\omega}{\omega_{0}}})^2} \tag{8.15} \]

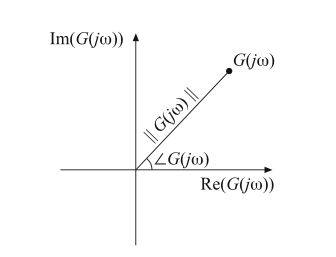
Fig. 8.5 Magnitude and phase of the complex-valued function \(G(jω)\)

在此我们假定\(\omega_{0}\)是实数，以分贝为单位时，幅值为：

\[||G(j\omega)||_{dB}=-20log_{10}(\sqrt{1+(\cfrac{\omega}{\omega_{0}})^2})\ dB \tag{8.16} \]

绘制\(G\)的bode图的一种简单方法就是分析较大频率与较小频率的渐进特性。

在频率较小时，\(\omega<<\omega_{0}\)，\(f<<f_{0}\)，那么有：

\[(\cfrac{\omega}{\omega_{0}})<<1 \tag{8.17} \]

因此，式(8.15)中的\((\omega/\omega_{0})^2\)远小于1，所以该式变为：

\[||G(j\omega)||\approx \cfrac{1}{\sqrt{1}}=1 \tag{8.18} \]

在对数上，幅值近似为：

\[||G(j\omega)||_{dB} \approx 0\ dB \tag{8.19} \]

因此，如图8.6，\(||G(j\omega)||_{dB}\)渐进为\(0\ dB\)。

在高频段，\(\omega>>\omega_{0}\)，\(f>>f_{0}\)，那么有：

\[(\cfrac{\omega}{\omega_{0}})>>1 \tag{8.20} \]

那么可以认为：

\[1+(\cfrac{\omega}{\omega_{0}})^2 \approx (\cfrac{\omega}{\omega_{0}})^2 \tag{8.21} \]

那么式(8.15)现在变为：

\[||G(j\omega)|| \approx \cfrac{1}{\sqrt{(\cfrac{\omega}{\omega_{0}})^2}}=(\cfrac{f}{f_{0}})^{-1} \tag{8.22} \]

这个表达式与\(n=-1\)时的式(8.5)是一致的。所以，如图8.6所示，在高频段\(||G(j\omega)||_{dB}\)斜率为\(-20\ dB\)每十倍频程。也就是，\(||G(j\omega)||\)低频渐进线为1，高频时为\((f/f_{0})^{-1}\)。渐近线的交截点频率为\(f_{0}\)。实际的幅值在频率较大和较小的时候趋近于上述的渐近线，而在转折频率\(f_{0}\)附近，实际幅值曲线与渐近线略有偏差。

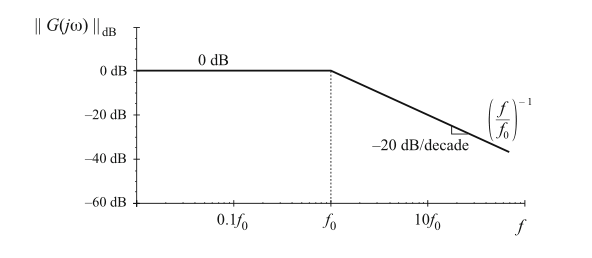
Fig. 8.6 Magnitude asymptotes for the single real pole transfer function

实际曲线与渐近线的偏差可以通过式(8.15)进行求解。在转折频率\(f=f_{0}\)时，时(8.15)变为：

\[||G(j\omega_{0})||=\cfrac{1}{1+(\cfrac{\omega}{\omega_{0}})^2}=\cfrac{1}{\sqrt{2}} \tag{8.23} \]

以分贝表示，该幅值为：

\[||G(j\omega_{0})||_{dB}=-20log_{10}(\sqrt{1+(\cfrac{\omega}{\omega_{0}})^2}) \approx -3\ dB \tag{8.24} \]

因此，如图8.7所示，实际曲线与渐近线在转折频率处偏差为\(-3\ dB\)。类似的方法可知，实际曲线与渐近线在\(f=f_{0}/2\)与\(f=2f_{0}\)处的偏差为\(-1\ dB\)。

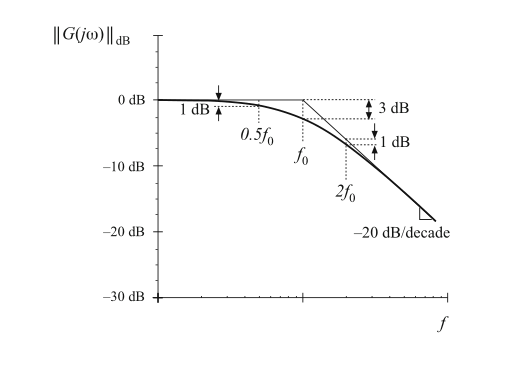
Fig. 8.7 Deviation of the actual curve from the asymptotes, real pole

\(G(j\omega)\)的相角为：

\[\angle G(j\omega)=tan^{-1}(\cfrac{Im(G(j\omega))}{Re(G(j\omega))}) \tag{8.25} \]

将(8.14)的实部和虚部代入上式，可以得到：

\[\angle G(j\omega)=-tan^{-1}(\cfrac{\omega}{\omega_{0}}) \tag{8.26} \]

这个函数如图8.8所示。其在低频趋近于0°，在高频趋近于-90°。在转折频率\(f=f_{0}\)处，相角为-45°。

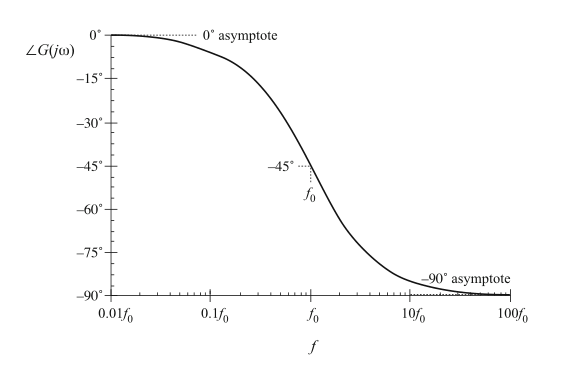
Fig. 8.8 Exact phase plot,real pole

由于高频与低频的相角渐进线并没有相交，我们还需要第三条渐进线来对转折频率\(f_{0}\)附近的相位进行近似。图8.9给出了一种方法，其中渐进线的斜率选择为\(f=f_{0}\)的实际曲线的斜率相同。可以证明，在这种选择的情况下，渐近线相交的频率\(f_{a}\)和\(f_{b}\)的频率为：

\[\begin{matrix} f_{a}=f_{0}e^{-\pi/2} \approx\cfrac{f_{0}}{4.81} \\ f_{b}=f_{0}e^{\pi/2} \approx 4.81f_{0} \tag{8.27} \end{matrix} \]

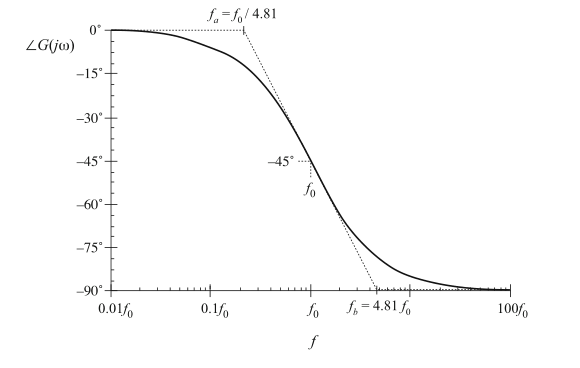
Fig. 8.9 One choice for the mid-frequency phase asymptote, which correctly predicts the actual slope at \(f=f_{0}\)

可以更好地逼近实际曲线的另一种方式是令：

\[\begin{matrix} f_{a}=\cfrac{f_{0}}{10} \\ f_{b}=10f_{0} \tag{8.28} \end{matrix} \]

这种渐进方式与实际曲线的对比如图8.10所示。极点导致了相位在以转折频率为中心的大约两个十倍频程跨度内变化。在这个频率范围内的渐近线的斜率为-45°每十倍频程。在拐点频率\(f_{a}\)和\(f_{b}\)处，实际相位于渐进线的偏差角度为\(tan^{-1}(0.1)=5.7°\)。

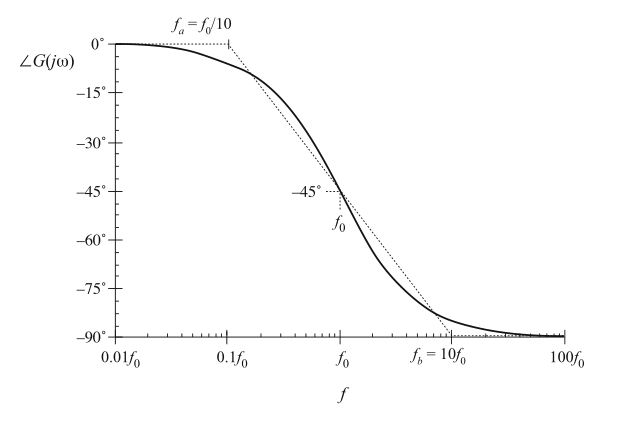
Fig. 8.10 A simpler choice for the mid-frequency phase asymptote, which better approximates the curve over the entire frequency range

图8.11整理了单极点响应的幅值和相角渐进曲线。比较好的习惯是始终以等式(8.12)的形式来表示单极传递函数。式(8.12)中分母中的两项都是无量纲的，并且\(s^{0}\)项的系数为单位1。由于是归一化的形式，式(8.12)很容易理解。在低频下，\((s/\omega_{0})\)在幅值上较小，传递函数近似为1。在高频\((s/\omega_{0})\)的幅值远大于1，传递函数近似为\((s/\omega_{0})^{-1}\)。那么其幅值为\((f/f_{0})^{-1}\)。转折频率\(f_{0}=\omega_{0}/2 \pi\)。因此传递函数是根据其显著特征(渐近线和转折频率)直接编写的。

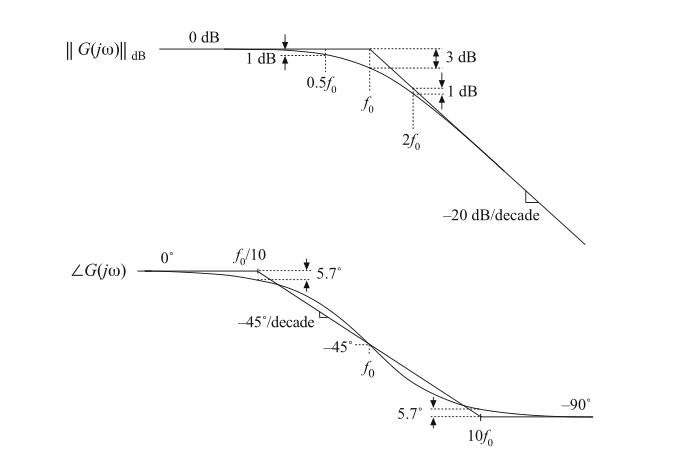
Fig. 8.11 Summary of the magnitude and phase Bode plot for the single real pole

8.1.2 单零点响应

单零点响应在传递函数的分子上包含一个根，并且可以写为如下的标准形式：

\[G(s)=(1+\cfrac{s}{\omega_{0}}) \tag{8.29} \]

这个传递函数的幅值为：

\[||G(j\omega)||=\sqrt{1+(\cfrac{\omega}{\omega_{0}})^2} \tag{8.30} \]

在低频段，\(f<<f_{0}=\omega_{0}/2\pi\)，传递函数的幅值为\(1 \Rightarrow 0\ dB\)。在高频段，\(f>>f_{0}\)，传递函数的幅值趋近于\((f/f_{0})\)。如图8.12所示，高频渐进线为\(+20\ dB\)每十倍频程。相角可以表示为：

\[\angle G(j\omega)=tan^{-1}(\cfrac{\omega}{\omega_{0}}) \tag{8.31} \]

除了负号以外，上式与式(8.26)完全一样。因此，渐近线如图8.12所示。在低频时，相位趋近于0°，高频时相位趋近于+90°。在区间\(f_{0}/10<f<10f_{0}\)内，相位渐近线的斜率为\(+45°\)每十倍频程。

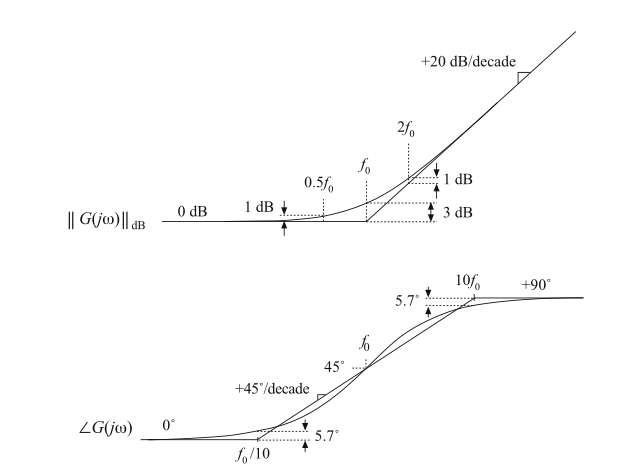
Fig. 8.12 Summary of the magnitude and phase Bode plot for the single real zero

8.1.3 右半平面零点

在开关变换器的小信号传递函数中经常会遇到右半平面零点。这些项通常具有以下的标准形式：

\[G(s)=(1-\cfrac{s}{\omega_{0}}) \tag{8.32} \]

式(8.32)的根为正值，因此其位于\(s\)复平面的右半平面。右半平面零点有时也被称为非最小相位零点。其标准化形式为(8.32)，除了\(s\)的系数的负号以外，与左半平面零点的标准形式相同。负号导致了高频处相位的反转。

传递函数的幅值为：

\[||G(j\omega)||=\sqrt{1+(\cfrac{\omega}{\omega_{0}})^{2}} \tag{8.33} \]

这个表达式与式(8.30)是相同的。因此，从幅值上来说，并不能将右半平面零点与左半平面零点分开。其相角为：

\[\angle G(j\omega)=-tan^{-1}(\cfrac{\omega}{\omega_{0}}) \tag{8.34} \]

这与式(8.26)的单极点的相位表达式相同。因此，右半平面零点呈现左半平面零点的幅值响应，但相角响应与左半平面极点相同。图8.13总结了其幅值和相角的渐近线。

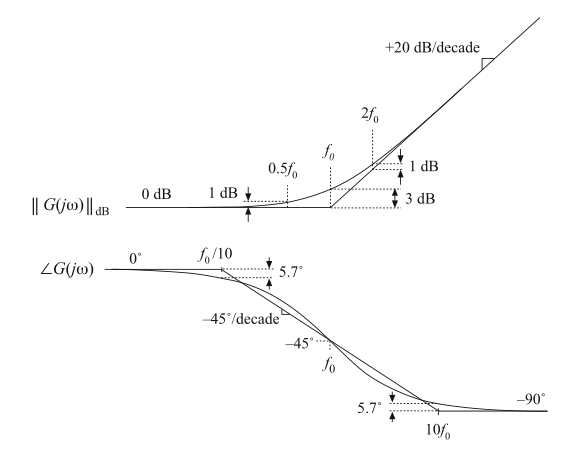
Fig. 8.13 Summary of the magnitude and phase Bode plot for the single real RHP zero

8.1.4 频率翻转

将现有的bode特性图高低频特性反转(译者：把传递函数中的\(s/\omega_{0}\)变为\(\omega_{0}/s\)，又可以得到额外的两种形式。翻转的单极点响应的传递函数为：

\[G(s)=\cfrac{1}{(1+\cfrac{\omega_{0}}{s})} \tag{8.35} \]

如图8.14，单极点响应翻转后的bode特性，高频增益为1，低频渐近线斜率为\(+20\ dB\)每十倍频程。这种形式可以用来描述那些高通滤波器的增益，以及在需要强调高频增益，低频衰减的其他传递函数的增益。式(8.35)等效于：

\[G(s)=\cfrac{(\cfrac{s}{\omega_{0}})}{(1+\cfrac{s}{\omega_{0}})} \tag{8.36} \]

但是，式(8.35)更直观的强调了高频增益为1的特性。

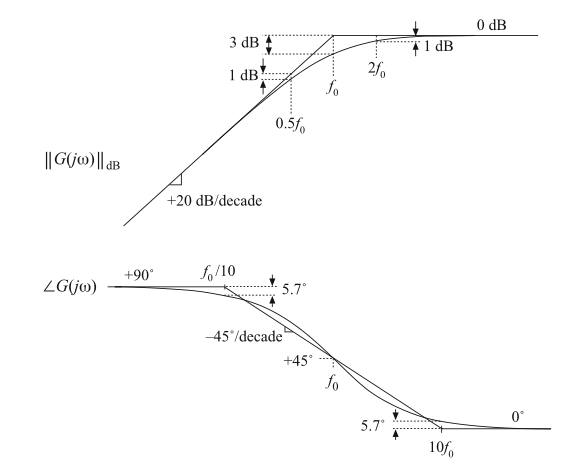
Fig. 8.14 Inversion of the frequency axis: summary of the magnitude and phase Bode plots for the
inverted real pole

将单零点传函bode图特性进行频率翻转后:

\[G(s)=(1+\cfrac{\omega_{0}}{s}) \tag{8.37} \]

如图8.15所示，将单零点传函bode图特性进行频率翻转后，高频增益渐进趋于1，而低频渐进斜率为\(-20\ dB\)每十倍频程。这种形式传递函数的一个应用就是PI控制器( proportional-plus-integral controller)，将在下一章中与反馈回路设计有关的内容里进行讨论。式(8.37)等效于：

\[G(s)=\cfrac{(1+\cfrac{s}{\omega_{0}})}{(\cfrac{s}{\omega_{0}})} \tag{8.38} \]

然而，当需要强调其高频增益渐进线时，式(8.37)是更好的选择。

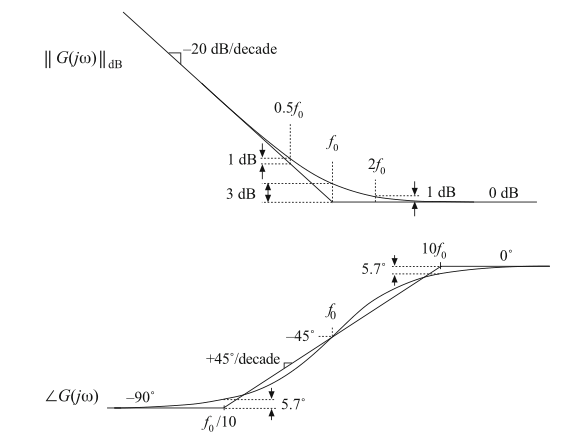
Fig. 8.15 Inversion of the frequency axis: summary of the magnitude and phase Bode plot for the inverted real zero

下一节将举例说明如何使用频率反转。

8.1.5 组合

对于包含若干个极点，零点以及增益项的传递函数的伯德图，可以通过简单的加法来构造。在任何给定的频率下，复合传递函数的大小(以分贝为单位)等于各个项分贝总和。同样的，在给定频率下，复合传递函数的相位也是各项相角之和。

例如，假设我们已经构建了两个关于\(\omega\)的复函数，\(G_{1}(\omega)\)和\(G_{2}(\omega)\)。这两个函数的幅值为\(R_{1}(\omega)\)，\(R_{2}(\omega)\)，相角为\(\theta_{1}(\omega)\)和\(\theta_{2}(\omega)\)。我们希望构建乘积项\(G_{3}(\omega)=G_{1}(\omega)G_{2}(\omega)\)。并且设\(G_{3}(\omega)\)的幅值和相角分别为\(R_{3}(\omega)\)和\(\theta_{3}(\omega)\)。为了求解这个幅值和相角，我们将\(G_{1}(\omega)\)，\(G_{2}(\omega)\)和\(G_{3}(\omega)\)写成极坐标的形式：

\[\begin{matrix} G_{1}(\omega)=R_{1}(\omega)e^{j\theta_{1}(\omega)} \\ G_{2}(\omega)=R_{2}(\omega)e^{j\theta_{2}(\omega)} \\ G_{3}(\omega)=R_{3}(\omega)e^{j\theta_{3}(\omega)} \tag{8.39} \end{matrix} \]

乘积项\(G_{3}(\omega)\)可以表示为：

\[G_{3}(\omega)=G_{1}(\omega)G_{2}(\omega)=R_{1}(\omega)e^{j\theta_{1}(\omega)}R_{2}(\omega)e^{j\theta_{2}(\omega)} \tag{8.40} \]

\[G_{3}(\omega)=(R_{1}(\omega)R_{2}(\omega))e^{j(\theta_{1}(\omega)+\theta_{2}(\omega))} \tag{8.41} \]

因此，相位为：

\[\theta_{3}(\omega)=\theta_{1}({\omega})+\theta_{2}(\omega) \tag{8.42} \]

总幅值为：

\[R_{3}(\omega)=R_{1}(\omega)R_{2}(\omega) \tag{8.43} \]

以分贝形式表示时，式(8.43)变为：

\[|R_{3}(\omega)|_{dB}=|R_{1}(\omega)|_{dB}+|R_{2}(\omega)|_{dB} \tag{8.44} \]

因此，复合后的传递函数，总相位为各个相位之和，以分贝表示时，总幅值就是各个幅值之和。所以，在以\(dB\)每十倍频程为单位时，总幅值的斜率也就是各个部分幅值斜率之和。

例如，考虑下面传递函数的bode图的构建：

\[G(s)=\cfrac{G_{0}}{(1+\cfrac{s}{\omega_{1}})(1+\cfrac{s}{\omega_{2}})} \tag{8.45} \]

其中\(G_{0}=40\ \Rightarrow\ 32dB\)，\(f_{1}=\omega_{1}/2\pi=100\ Hz\)，\(f_{2}=\omega_{2}/2\pi=2\ kHz\)。该传递函数包含三个部分：增益\(G_{0}\)，以及频率为\(f_{1}\)和\(f_{2}\)的两个极点。图8.16给出了其中各项的渐进线。\(G_{0}\)是一个正实数，因此其增益为\(32\ dB\)并且对相位无影响。在\(100\ Hz\)和\(2\ kHz\)处分别产生了如图8.11所示的渐近线。

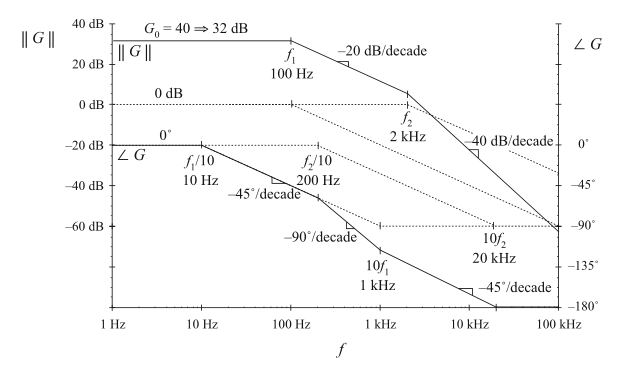
Fig. 8.16 Construction of magnitude and phase asymptotes for the transfer function of Eq. (8.45). Dashed lines: asymptotes for individual terms. Solid lines: composite asymptotes

在频率小于\(100\ Hz\)时。\(G_{0}\)项贡献的幅值增益为\(32\ dB\)，其他两个极点的渐近线均为\(0\ dB\)。所以，低频总幅值渐进线为\(32\ dB\ +\ 0\ dB\ +\ 0\ dB=\ 32\ dB\)。在位于\(100\ Hz\)到\(2\ kHz\)的频率范围内，\(G_{0}\)仍贡献\(32\ dB\)的增益，\(2\ kHz\)单极点项幅值渐近仍然为\(0\ dB\)，只不过这时\(100\ Hz\)处单极点项的幅值斜率已经是\(-20\ dB\)每十倍频程。如图8.16，总幅值的渐近线也会以\(-20\ dB\)每十倍频程下降。在大于\(2\ kHz\)的频率范围内，\(100\ Hz\)和\(2\ kHz\)的单极点幅值渐近线斜率均为\(-20\ dB\)每十倍频程。如图所示，总的幅值渐近线就以\(-40\ dB\)每十倍频程下降。

图8.16还给出了总相位渐进线。在\(10\ Hz\)以下，各部分的相位渐进线都是0°。在\(f_{1}/10=10\ Hz\)到\(f_{2}/10=200\ Hz\)频率范围内，\(f_{1}\)处的极点使得相位以\(-45°\)每十倍频程递减。在\(200\ Hz\)到\(10f_{1}=1\ kHz\)频率范围内，两个极点贡献的斜率均为\(-45°\)每十倍频程，总斜率为\(-90°\)每十倍频程。在\(1\ kHz\)到\(10f_{2}=\ 20\ kHz\)范围内，\(f_{1}\)处的极点贡献的相角渐近线恒为\(-90°\)，而\(f_{2}\)处极点造成的相位渐近线斜率为\(-45°\)每十倍频程。所以这段频率范围内，总斜率为\(-45°\)每十倍频程。对于大于\(20\ kHz\)的频率范围，两个极点贡献的相位渐近线均为\(-90°\)。因此，总相位渐近线为\(-180°\)。

作为第二个示例，考虑图8.17所示的幅值和渐近线表示的传递函数\(A(s)\)。让我们来写出这些渐近线对应的传递函数。直流渐近线为\(A_{0}\)。在转折频率\(f_{1}\)处，渐近线斜率从\(0\ dB\)增加到\(+20\ dB\)每十倍频程。因此，在\(f_{1}\)处一定存在一个零点。在频率\(f_{2}\)处，渐近线斜率从\(+20\ dB\)减小到\(0\ dB\)每十倍频程。因此，传递函数包含一个频率为\(f_{2}\)的极点。所以我们可以将传递函数表示为：

\[A(s)=A_{0} \cfrac{(1+\cfrac{s}{\omega_{1}})}{(1+\cfrac{s}{\omega_{2}})} \tag{8.46} \]

其中\(\omega_1\)和\(\omega_{2}\)分别等于\(2\pi f_{1}\)和\(2\pi f_{2}\)。

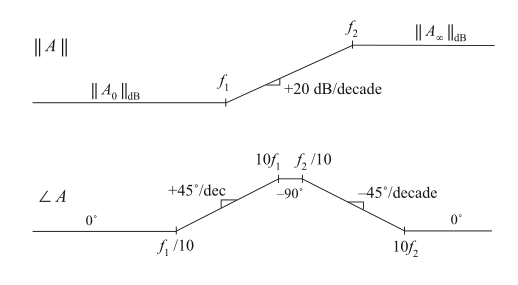
Fig. 8.17 Magnitude and phase asymptotes of example transfer function A(s)

我们可以利用式(8.46)来推导渐近线的表达式。对\(f<f_{1}\)，让\(s=j\omega\)，我们可以看到\((s/\omega_{1})\)和\((s/\omega_{2})\)的幅值都小于1。那么分析渐近线时就忽略这些项。因此，低频幅值渐近线为：

\[||A_{0} \cfrac{(1+\cfrac{s}{\omega_{1}})}{(1+\cfrac{s}{\omega_{2}})}||=A_{0} \cfrac{1}{1}=A_{0} \tag{8.47} \]

当\(f_{1}<f<f_{2}\)，分子项\((s/\omega_{1})\)幅值大于1，而分母项\((s/\omega_{2})\)幅值小于1。对于渐近线，可以通过忽略较小项来推导：

\[||A_{0} \cfrac{(1+\cfrac{s}{\omega_{1}})}{(1+\cfrac{s}{\omega_{2}})}||=A_{0} \cfrac{||\cfrac{s}{\omega_{1}}||_{s=j\omega}}{1} \\ =A_{0} \cfrac{\omega}{\omega_{1}}=A_{0} \cfrac{f}{f_{1}} \tag{8.48} \]

这就是\(A(s)\)的中频幅值渐近线的表达式。对\(f>f_{2}\)频段，\((s/\omega_{1})\)和\((s/\omega_{2})\)的幅值都大于1。高频渐近线的表达式为：

\[||A_{0} \cfrac{(1+\cfrac{s}{\omega_{1}})}{(1+\cfrac{s}{\omega_{2}})}||=A_{0} \cfrac{||\cfrac{s}{\omega_{1}}||_{s=j\omega}}{||\cfrac{s}{\omega_{2}}||_{s=j\omega}} =A_{0} \cfrac{\omega_{2}}{\omega_{1}}=A_{0} \cfrac{f_{2}}{f_{1}} \tag{8.49} \]

总结下，高频增益为：

\[A_{\infty}=A_{0} \cfrac{f_{2}}{f_{1}} \tag{8.50} \]

因此我们可以就可以得到渐近线的表达式了。

利用极点和零点的翻转，还可以将\(A(s)\)写成另一种形式。假设\(A(s)\)代表高频放大器的传递函数，其直流增益并不重要。然后，我们期望使用高频增益\(A_{\infty}\)来表示\(A(s)\)。可以将传递函数视为在频率\(f_{2}\)处有一个翻转的极点，这会在小于\(f_{2}\)频率处引起幅值衰减。此外，在\(f=f_{1}\)频率处，还有一个翻转的零点。因此\(A(s)\)可以表示为：

\[A(s)=A_{\infty} \cfrac{(1+\cfrac{\omega_{1}}{s})}{(1+\cfrac{\omega_{2}}{s})} \tag{8.51} \]

可以验证，式(8.51)和(8.46)是等效的。

8.1.6 双极点响应：谐振

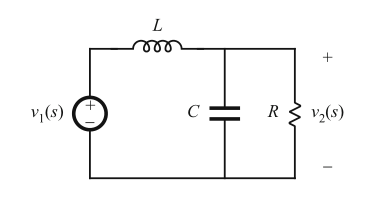
Fig. 8.18 Two-pole low-pass filter example

接下来考虑图8.18所示的双极点低通滤波器的传递函数\(G(s)\)。降压变换器就包含此类低通滤波器(输出的LC滤波器)。当转化为规范形式时，boost和buck-boost变换器的模型中也包含类似的变换器。可以看出，该电网络的传递函数为：

\[G(s)=\cfrac{v_{2}(s)}{v_{1}(s)}=\cfrac{1}{1+s \cfrac{L}{R}+s^{2}LC} \tag{8.52} \]

该传递函数的分母包含一个二阶多项式，其形式为：

\[G(s)=\cfrac{1}{1+a_{1}s+a_{2}s^{2}} \tag{8.53} \]

其中，\(a_{1}=L/R\)，\(a_{2}=LC\)。

要构建这个传递函数的bode图，我们可以尝试将分母分解为两个根乘积形式：

\[G(s)=\cfrac{1}{(1-\cfrac{s}{s_{1}})(1-\cfrac{s}{s_{2}})} \tag{8.54} \]

利用二次方程求根公式可以得到：

\[\begin{matrix} s_{1}=-\cfrac{a_{1}}{2a_{2}}[1-\sqrt{1-\cfrac{4a_{2}}{a_{1}^{2}}}] \\ s_{2}=-\cfrac{a_{1}}{2a_{2}}[1+\sqrt{1-\cfrac{4a_{2}}{a_{1}^{2}}}] \tag{8.55-56} \end{matrix} \]

如果\(4a_{2} \leq a_{1}^{2}\)，那么根为实数。每一个实极点都如8.1.1节展现出相应的bode特性，并且复合的bode图可以根据8.1.5节的描述来构建(但8.1.7节给出了一种更好的方法)。

如果\(4a_{2}>a_{1}^{2}\)，那么式(8.55)和(8.56)的解为复数。在第8.1.1节中，以\(\omega_{0}\)是实数进行假设，因此，该节的结果并不能用于这里的情况。我们需要在根为复数的情况下做一些额外的工作来确定幅值和相角。式(8.52)和(8.53)可以用以下的标准形式重新写出：

\[G(s)=\cfrac{1}{1+2\zeta \cfrac{s}{\omega_{0}}+(\cfrac{s}{\omega_{0}})^{2}} \tag{8.57} \]

如果系数\(a_{1}\)和\(a_{2}\)是正实数，那么参数\(\zeta\)和\(\omega_{0}\)也是正实数。参数\(\omega_{0}\)仍然是转折频率，并且我们定义\(f_{0}=\omega_{0}/2 \pi\)。参数\(\zeta\)被称为阻尼系数：\(\zeta\)控制了\(f=f_{0}\)附近的传递函数特性的形状。另一种标准形式为：

\[G(s)=\cfrac{1}{1+\cfrac{s}{Q \omega_{0}}+(\cfrac{s}{\omega_{0}})^{2}} \tag{8.58} \]

其中

\[Q=\cfrac{1}{2\zeta} \tag{8.59} \]

参数\(Q\)被称为电路的品质因数，并且可以衡量系统的耗散程度。对于无源元件或者网络的正弦激励，\(Q\)的更一般的定义为：

\[Q=2\pi \cfrac{(peak\ stored\ energy)}{(energy\ dissipated\ per\ cycle)} \tag{8.60} \]

对于二阶无源系统，式(8.59)和(8.60)是等效的。我们将会看到，在二阶传递函数的幅值bode特性上，系数\(Q\)具有非常简单的定义。

参数\(Q\)和\(\omega_{0}\)的解析表示可以通过令式(8.52)的原始传递函数和标准式(8.58)的同次幂式对比得到。其结果为：

\[\begin{cases} f_{0}=\cfrac{\omega_{0}}{2\pi}=\cfrac{1}{2\pi \sqrt{LC}} \\ Q=R \sqrt{\cfrac{C}{L}} \tag{8.61} \end{cases} \]

当\(Q \leq 0.5\)时，式(8.55)和(8.56)的根\(s_{1}\)和\(s_{2}\)为实数，并且当\(Q>0.5\)时为复数。

\(G\)的幅值为：

\[||G(j\omega)||=\cfrac{1}{\sqrt{(1-(\cfrac{\omega}{\omega_{0}})^{2})^{2}+\cfrac{1}{Q^{2}}(\cfrac{\omega}{\omega_{0}})^2}} \tag{8.62} \]

图8.19给出了\(||G||\)的渐近线。在低频段，\((\omega / \omega_{0})<<1\)，因此：

\[||G|| \rightarrow 1\ \ \ for\ \omega<<\omega_{0} \tag{8.63} \]

在高频段，\((\omega / \omega_{0})>>1\)，\((\omega /\omega_{0})^{4}\)项主导了根式内部的结果(译者：也就是根式值取决于该项)，因此，高频渐进线为：

\[||G|| \rightarrow(\cfrac{f}{f_{0}})^{-2} \ \ \ for\ \omega>>\omega_{0} \tag{8.64} \]

这个表达式与\(n=-2\)时的式(8.5)是等效的。因此其高频渐近线斜率为\(-40\ dB\)每十倍频程。渐近线的交截点再\(f=f_{0}\)，并且与\(Q\)无关。

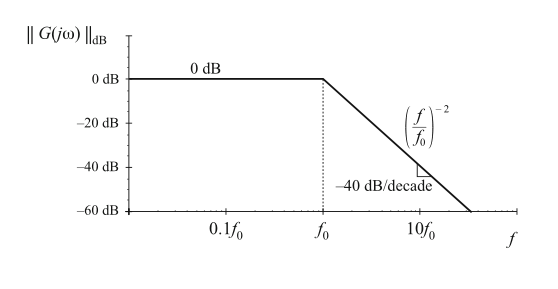
Fig. 8.19 Magnitude asymptotes for the two-pole transfer function

参数\(Q\)实际影响着转折频率\(f_{0}\)附近实际曲线与渐近线之间的偏差。在\(f=f_{0}\)处的实际幅值可以将\(\omega=\omega_{0}\)代入式(8.62)得到：

\[||G(j\omega_{0})||=Q \tag{8.65} \]

所以实际传递函数在转折频率\(f_{0}\)处的幅值为\(Q\)。以分贝表示时，式(8.65)变为：

\[||G(j\omega_{0})||_{dB}=|Q|_{dB} \tag{8.66} \]

因此，现在如果假设\(Q=2 \Rightarrow6\ dB\)，那么实际曲线与渐近线在转折频率\(f=f_{0}\)处的偏差就达到了\(6dB\)。图8.20给出了二阶传递函数幅值bode图的显著特征。

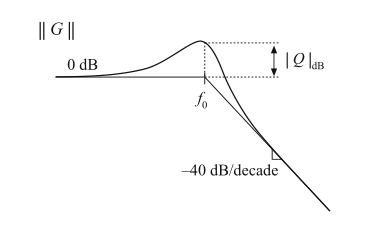
Fig. 8.20 Important features of the magnitude Bode plot, for the two-pole transfer function

\(G\)的相位为：

\[\angle G(j\omega)=-tan^{-1} [\cfrac{\cfrac{1}{Q}(\cfrac{\omega}{\omega_{0}})}{1-(\cfrac{\omega}{\omega_{0}})^{2}}] \tag{8.67} \]

在低频段，相角趋近于0°，在高频段趋近于-180°。在\(f=f_{0}\)处，相角为-90°。如图8.21，\(Q\)值的增加使得0°与-180°渐近线之间的相位改变更加陡峭。这里我们仍然需要一个中频渐近线，来近似转折频率\(f_{0}\)附近的相角变化，如图8.22所示。在实际中为单极点的情况时，我们可以将渐近线的斜率设置为与\(f=f_{0}\)时实际曲线的斜率相同。可以证明，这种选择会得到以下渐近线的穿越频率：

\[\begin{matrix} f_{a}=(e^{\pi /2})^{- \frac{1}{2Q}}f_{0} \\ f_{a}=(e^{\pi /2})^{ \frac{1}{2Q}}f_{0} \tag{8.68} \end{matrix} \]

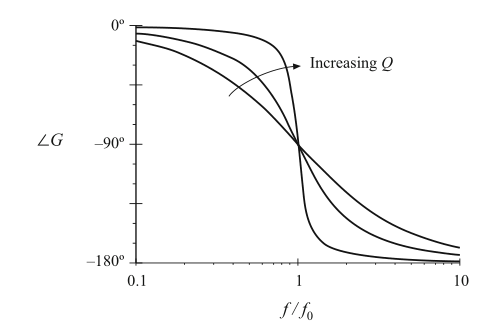
Fig. 8.21 Phase plot, second-order poles. Increasing Q causes a sharper phase change

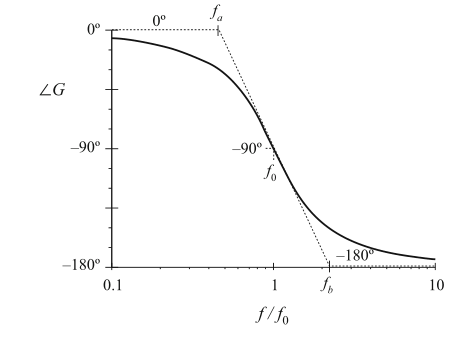
Fig. 8.22 One choice for the mid-frequency phase asymptote of the two-pole response, which
correctly predicts the actual slope at \(f = f_{0}\)

作为另一种更好的近似选择，可以与式(8.28)采用的对实极点的近似方法保持一致：

\[\begin{matrix} f_{a}=10^{-\frac{1}{2Q}}f_{0} \\ f_{b}=10^{\frac{1}{2Q}}f_{0} \tag{8.69} \end{matrix} \]

在这种情况下，中频渐近线的斜率为\(-180Q°\)每十倍频程。相位渐近线如图8.23所示。在\(Q=0.5\)的情况下，以转折频率\(f_{0}\)为中心，在大约二十倍频程的跨度内，相位从0°变为-180°。增加\(Q\)会使这个频率跨度范围迅速降低。

图8.24和8.25绘制了二阶响应的幅值和相位曲线。

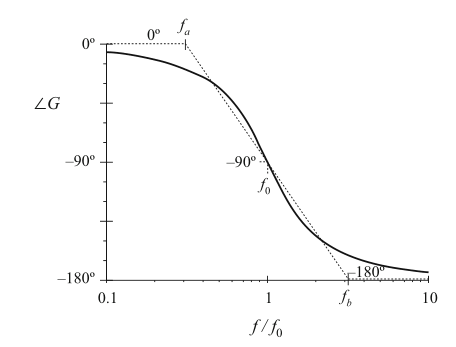
Fig. 8.23 A simpler choice for the mid-frequency phase asymptote, which better approximates the curve over the entire frequency range and is consistent with the asymptote used for real poles

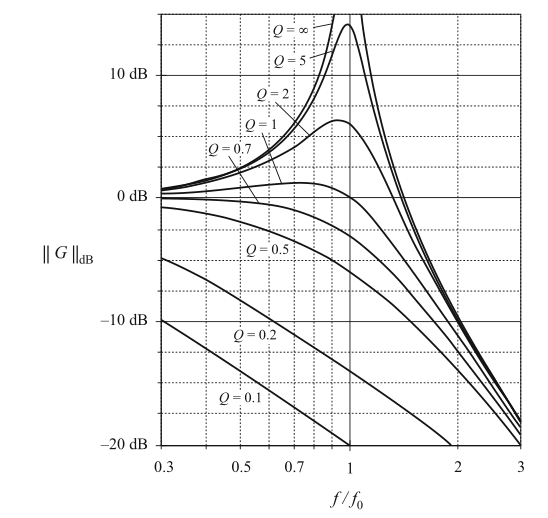
Fig. 8.24 Exact magnitude curves, two-pole response, for several values of Q

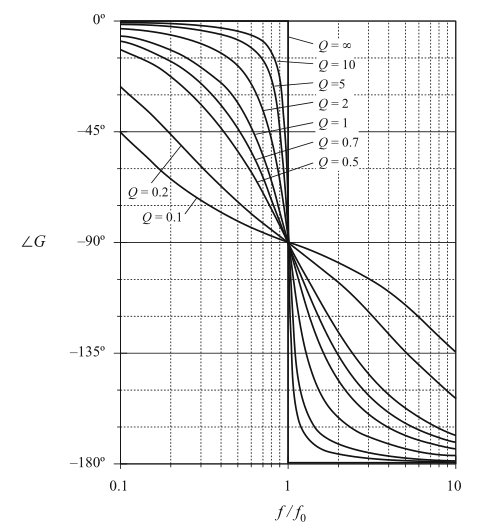
Fig. 8.25 Exact phase curves, two-pole response, for several values of Q

8.1.7 低\(Q\)值逼近

正如8.1.6节所述，当式(8.53)的二阶分母多项式的根为实数时，那么我们就可以分解分母，并使用渐近线来构造实极点的bode图。我们可以使用如下的标准形式：

\[G(s)=\cfrac{1}{(1+\cfrac{s}{\omega_{1}})(1+\cfrac{s}{\omega_{2}})} \tag{8.70} \]

当转折频率\(\omega_{1}\)和\(\omega_{2}\)分隔较远时，这是比较理想的方法。

这个过程的困难之处在于用于确定转折频率的二次方程的复杂性。特别是当电路包含元件较多时，用电路元件\(R,L,C\)等来表示转折频率\(\omega_{1}\)和\(\omega_{2}\)总是得到复杂且模糊的表述公式。即使在传递函数由式(8.52)给出的如图8.18所示的简单电路中，常规的二次方程使得转折频率如下式般复杂：

\[\omega_{1},\omega_{2}=\cfrac{\cfrac{L}{R} \pm \sqrt{(\cfrac{L}{R})^{2}-4LC}}{2LC} \tag{8.71} \]

对于转折频率与这些元件值之间的关系，上式并不能给出比较直观的结果。打个比方，可以证明，当转折频率的值分隔较远时，可以通过更简单的关系来高精度的表示他们：

\[\omega_{1} \approx\cfrac{R}{L},\ \ \ \omega_{2}=\cfrac{1}{RC} \tag{8.72} \]

在这种情况下，\(\omega_{1}\)基本上与\(C\)的值无关，而\(\omega_{2}\)的值基本上与\(L\)无关。而式(8.71)显然显示两个转折频率都与所有元件值有关。式(8.72)的简化公式比(8.71)更适合，并且其可以很容易的利用低\(Q\)近似得到。

让我们假设传递函数已经以式(8.58)的标准形式写出，这里再次给出：

\[G(s)=\cfrac{1}{1+\cfrac{s}{Q \omega_{0}}+(\cfrac{s}{\omega_{0}})^{2}} \tag{8.73} \]

当\(Q<0.5\)时，我们使用二次方程求根公式写出实根：

\[\begin{matrix} \omega_{1}=\cfrac{\omega_{0}}{Q} \cfrac{1-\sqrt{1-4Q^2}}{2} \\ \omega_{1}=\cfrac{\omega_{0}}{Q} \cfrac{1+\sqrt{1-4Q^2}}{2} \tag{8.74-75} \end{matrix} \]

转折频率\(\omega_{2}\)可以表示为：

\[\omega_{2}=\cfrac{\omega_{0}}{Q}F(Q) \tag{8.76} \]

其中将\(F(Q)\)定义为：

\[F(Q)=\cfrac{1}{2}(1+\sqrt{1-4Q^2}) \tag{8.77} \]

注意到，当\(Q<<0.5\)时，\(4Q^2<<1\)，那么\(F(Q)\)就近似等于1。我们可以得到：

\[\omega_{2} \approx \cfrac{\omega_{0}}{Q} \ \ for\ Q<<0.5 \tag{8.78} \]

\(F(Q)\)的函数如图8.26所示。可以看出，当\(Q\)降低到0.5以下时，\(F(Q)\)很快接近于1。

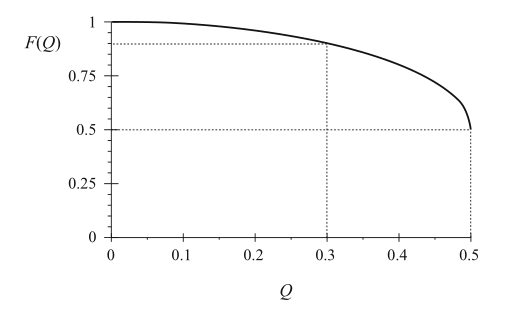
Fig. 8.26 F(Q) v s. Q, as given by Eq . (8.77). The approximation F(Q) = 1 is within 10% of the exact value for Q < 0.5

为了得到\(\omega_{1}\)的近似值，我们将式(8.74)先乘(8.77)的\(F(Q)\)，展开化简后，再除以\(F(Q)\)。通过简化我们得到：

\[\omega_{1}=\cfrac{Q\omega_{0}}{F(Q)} \tag{8.79} \]

同样的，当\(Q\)较小时，\(F(Q)\)趋近于1。因此，\(\omega_{1}\)可以近似为：

\[\omega_{1} \approx Q\omega_{0}\ \ \ for\ Q<<0.5 \tag{8.80} \]

图8.27给出了低\(Q\)情况下的幅值渐近线。当\(Q<0.5\)时，\(\omega_{0}\)处的两个极点分裂成实数极点。一个极点出现在转折频率\(\omega_{1}<\omega_{0}\)处，另一个出现在转折频率\(\omega_{2}>\omega_{0}\)处。使用式(8.78)和(8.80)可以很容易估算转折频率。

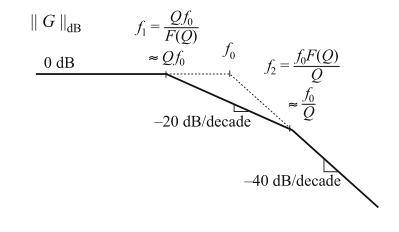
Fig. 8.27 Magnitude asymptotes predicted by the low-Q approximation. Real poles occur at frequencies\(Qf_0\) and$ f_0/Q$

对于如图8.18所示的滤波器电路，参数\(Q\)和\(\omega_{0}\)由式(8.61)给出。当\(Q<<0.5\)时，我们可以利用式(8.78)和(7.80)推导出如下所示的转折频率的解析表达式：

\[\begin{matrix} \omega_{1} \approx Q\omega_{0}=R\sqrt{\cfrac{C}{L}} \cfrac{1}{\sqrt{LC}}=\cfrac{R}{L} \\ \omega_{2} \approx \cfrac{\omega_{0}}{Q}=\cfrac{1}{\sqrt{LC}} \cfrac{1}{R\sqrt{\cfrac{C}{L}}} =\cfrac{1}{RC} \tag{8.81} \end{matrix} \]

因此，低\(Q\)值逼近允许我们推导面向设计的转折频率的简化解析表达式。

8.1.8 高\(Q\)值逼近

另一个有趣的情况是确定含多个电阻元件的高\(Q\)值谐振电路的\(Q\)系数。例如，考虑图8.28所示的含负载电阻\(R\)和电容串联电阻\(R_{C}\)的LC谐振电路。在较大\(R\)和小\(R_{C}\)的情况下，电路近似为无阻尼LC电路，谐振频率为：

\[\omega_{0}=\cfrac{1}{\sqrt{LC}} \tag{8.82} \]

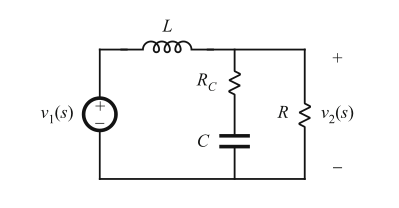
Fig. 8.28 Two-pole low-pass filter with two resistive elements

当\(R_{C}\)小到可以忽略而\(R\)又很大时，这个电路已经在先前的8.1.6节中讨论过了(图8.18)。先前我们已经得到了该电路的\(Q\)系数：

\[Q_{load}=\cfrac{R}{R_{0} }\tag{8.83} \]

其中：

\[R_{0}=\sqrt{\cfrac{L}{C}} \]

那么传递函数为：

\[G(s)=\cfrac{1}{1+\cfrac{s}{Q_{load}\omega_{0}}+(\cfrac{s}{\omega_{0}})^{2}} \tag{8.84} \]

相反，当负载电阻\(R\)较大但同时\(R_{C}\)也比较显著时，我们可以分析电路并找到如下所示的传递函数：

\[G(s)=\cfrac{(1+\cfrac{s}{\omega_{z}})}{1+\cfrac{s}{Q_{c}\omega_{0}}+(\cfrac{s}{\omega_{0}})^2} \tag{8.85} \]

转折频率\(\omega_{0}\)由式(8.82)，但\(Q\)系数为：

\[Q_{C}=\cfrac{R_{0}}{R_{C}} \tag{8.86} \]

因此这两种阻尼情况分别导致相似的二阶分母，其中的\(Q\)系数取决于电阻值。

对于\(R\)和\(R_{C}\)同时引起显著阻尼的情况下，我们可以分析图8.28所示的电路来推导传递函数：

\[G(s)=\cfrac{1+sR_{C}C}{1+s(\cfrac{L}{R}+R_{C}C)+s^{2}LC(1+\cfrac{R_{C}}{R})} \tag{8.87} \]

该式子可以被表示为如下所示的标准形式：

\[G(s)=\cfrac{(1+\cfrac{s}{\omega_{z}})}{1+(\cfrac{s}{\omega_{0}})(\cfrac{1}{Q_{load}}+\cfrac{1}{Q_{C}})+(\cfrac{s}{\omega_{0}})^{2}(1+\cfrac{1}{Q_{load}Q_{C}})} \tag{8.88} \]

其中：

\[\begin{matrix} \omega_{0}=\cfrac{1}{\sqrt{LC}} \\ Q_{load}=\cfrac{R}{R_{0}} \\ Q_{C}=\cfrac{R_{0}}{R_{C}} \\ R_{0}=\sqrt{\cfrac{L}{C}} \tag{8.89} \end{matrix} \]

如果\(Q_{load}>>1\)且\(Q_{C}>>1\)，那么：

\[1+\cfrac{1}{Q_{load}Q_{C}} \approx 1 \tag{8.90} \]

式(8.88)可以简化如下所示：

\[G(s) \approx\cfrac{(1+\cfrac{s}{\omega_{z}})}{1+(\cfrac{s}{\omega_{0}})(\cfrac{1}{Q_{load}||Q_{C}})+(\cfrac{s}{\omega_{0}})^{2}} \tag{8.91} \]

因此，对于\(R\)和\(R_{C}\)同时引起显著阻尼的情况，可以使用高\(Q\)值逼近根据\(Q_{load}\)和\(Q_{C}\)来估算复合\(Q\)因子：

\[Q\approx Q_{load}||Q_{C}=\cfrac{1}{\cfrac{1}{Q_{load}}+\cfrac{1}{Q_{C}}} \tag{8.92} \]

其中符号\(x||y\)代表并联结果，也就是倒数相加再取倒数。分母的这种极点近似是准确的，只要满足如下式子：

\[Q_{load}>>1\ \ and\ \ Q_{C}>>1 \tag{8.93} \]

两个阻尼项\(Q_{load}\)和\(Q_{C}\)同时影响精确的频率和\(Q\)系数。我们可以用下面的标准形式来表示式(8.88):

\[G(s) \approx\cfrac{(1+\cfrac{s}{\omega_{z}})}{1+(\cfrac{s}{\omega_{e}})(\cfrac{1}{Q_e})+(\cfrac{s}{\omega_{e}})^{2}} \tag{8.91} \]

其中精确的转折频率\(\omega_{e}\)和\(Q\)系数\(Q_{e}\)为：

\[\omega_{e}= \cfrac{\omega_{0}}{F_{H}(Q_{load}Q_{C})},\ \ Q_{e}=(Q_{load}||Q_{C})F_{H}(Q_{load}Q_{C}) \tag{8.95} \]

并且：

\[F_{H}(Q_{1}Q_{2})=\sqrt{1+\cfrac{1}{Q_{1}Q_{2}}} \tag{8.96} \]

系数\(F_{H}(Q_{1}Q_{2})\)如图8.29所示。可以看到，当两个\(Q\)因子的乘积增加到1以上时，这个系数收敛到1。

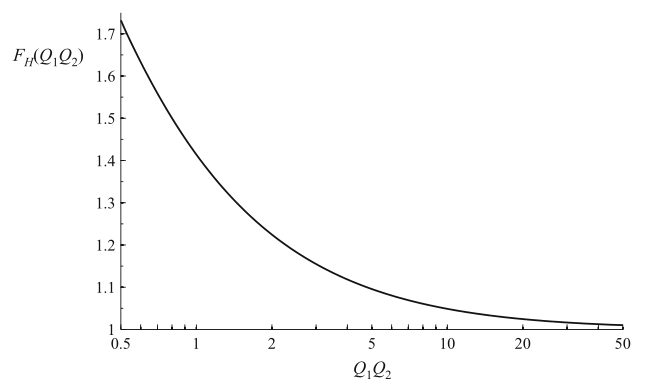
Fig 8.29 \(F_{H}(Q_{1}Q_{2})\) vs. \(Q_{1}Q_{2}\) as given by Eq.(8.96). The approximation \(F_{H}(Q_{1}Q_{2}) \approx 1\) is within 10% of the correct value for \(Q_{1}Q_{2}>5\)

综上所述，高\(Q\)值逼近表示在由两个分别引起\(Q_{1}\)和\(Q_{2}\)的元件构成的谐振电路中，其复合\(Q\)系数为\(Q_{1}||Q_{2}\)。这种近似方式有利于推导具有多个阻尼元件的面向设计的谐振电路简化表达式。第9.5.4节中给出了一个示例，其中高\(Q\)逼近大大简化了对电感和电容上的电阻都进行建模的buck变换器的模型方程。

8.1.9 任意阶多项式的近似根

我们还可以将低\(Q\)逼近法进行推导，来求解\(n\)阶多项式的近似解析表达式。

\[P(s)=1+a_{1}s+a_{2}s^2+...+a_{n}s^{n} \tag{8.97} \]

我们期望将上述多项式分解为如下形式：

\[P(s)=(1+\tau_{1}s)(1+\tau_{2}s)...(1+\tau_{n}s) \tag{8.98} \]

在实际电路中，系数\(a_{1},...a_{n}\)是实数，而时间常数\(\tau_{1},...\tau_{n}\)可能为实数也可能为复数。通常，部分或者所有的时间常数都可以很好的分隔开，并且会比较简单的依赖于电路元件的值。在这种情况下，可以推导出时间常数的简化近似解析表达式。

通过将式(8.98)乘开，可以将时间常数\(\tau_{1},...\tau_{n}\)用原始系数\(a_{1},...a_{n}\)来表示，其结果为：

\[\begin{aligned} & a_{1}=\tau_{1}+\tau_{2}+...+\tau_{n} \\ & a_{2}=\tau_{1}(\tau_{2}+...+\tau_{n})+\tau_{2}(\tau_{3}+...+\tau_{n})... \\ & a_{3}=\tau_{1}\tau_{2}(\tau_{3}+...+\tau_{n})+\tau_{2}\tau_{3}(\tau_{4}+...+\tau_{n})... \\ & ...\\ & a_{n}=\tau_{1}\tau_{2}\tau_{3}...\tau_{n} \end{aligned} \tag{8.99} \]

这个方程组的一般解等于任意阶多项式精确分解，这是一个非常困难的问题。但是，式(8.99)确实提出了一种近似根的方法。

假设所有的时间常数\(\tau_{1},...\tau_{n}\)都是实数并且值完全分开(译者：无重根)。我们可以不失一般性的进一步假设，将时间常数按降序排列：

\[|\tau_{1}|>>|\tau_{2}|>>...|\tau_{n}| \tag{8.100} \]

当式(8.100)的不等式满足时，那么式(8.99)中的\(a_{1},...a_{n}\)表达式均以各自的第一项为主导项：

\[\begin{aligned} & a_{1} \approx \tau_{1}\\ & a_{2} \approx \tau_{1} \tau_{2} \\ & a_{3} \approx \tau_{1} \tau_{2} \tau_{3} \\ &... \\ & a_{n} \approx \tau_{1} \tau_{2} \tau_{3}...\tau_{n} \\ \end{aligned} \tag{8.101} \]

现在可以利用时间常数求解这些表达式，结果为：

\[\begin{aligned} & \tau_{1} \approx a_{1} \\ & \tau_{2} \approx \cfrac{a_{2}}{a_{1}} \\ & \tau_{3} \approx \cfrac{a_{3}}{a_{2}} \\ & ...\\ & \tau_{n} \approx \cfrac{a_{n}}{a_{n-1}} \\ \end{aligned} \tag{8.102} \]

因此，如果：

\[|a_{1}|>>|\cfrac{a_{2}}{a_{1}}|>>|\cfrac{a_{3}}{a_{2}}|>>...>>|\cfrac{a_{n}}{a_{n-1}}| \tag{8.103} \]

然后由等式(8.97)给出的多项式\(P(s)\)可以具有近似因式分解：

\[P(s)\approx(1+a_{1}s)(1+\cfrac{a_{2}}{a_{1}}s)(1+\cfrac{a_{3}}{a_{2}}s)...(1+\cfrac{a_{n}}{a_{n-1}}s) \tag{8.104} \]

请注意，如果式(8.97)中的原始系数是电路元件的简单函数，那么由(8.104)给出的近似根也同样是类似的电路元件的简单函数。那么就可以获得根的近似解析表示。将数值代入式(8.103)可以证明近似的合理性。

当两个根并没有相距很远时，式(8.103)的不等式中就要有不满足的情况存在。这时，我们将相应的项保留为二次形式。假设第\(k\)个不等式不满足：

\[|a_{1}|>>|\cfrac{a_{2}}{a_{1}}|>>...>>|\cfrac{a_{k}}{a_{k-1}}| \not >> |\cfrac{a_{k+1}}{a_{k}}|...>>|\cfrac{a_{n}}{a_{n-1}}| \tag{8.105} \]

然后将其近似分解为：

\[P(s) \approx (1+a_{1}s)(1+ \cfrac{a_{2}}{a_{1}}s)...(1+\cfrac{a_{k}}{a_{k-1}}s+\cfrac{a_{k+1}}{a_{k-1}}s^{2})...(a+\cfrac{a_{n}}{a_{n-1}}s) \tag{8.106} \]

要保证上式的精确性，需要满足：

\[|a_{1}|>>|\cfrac{a_{2}}{a_{1}}|>>...>>|\cfrac{a_{k}}{a_{k-1}}| >>|\cfrac{a_{k-2}a_{k+1}}{a_{k-1}^2}|>>|\cfrac{a_{k+2}}{a_{k+1}}|...>>|\cfrac{a_{n}}{a_{n-1}}| \tag{8.107} \]

复杂的共轭根可以用这种形式简化。

当式(8.103)的第一个不等式不满足时：

\[|a_{1}|\not >>|\cfrac{a_{2}}{a_{1}}|>>|\cfrac{a_{3}}{a_{2}}|>>...>>|\cfrac{a_{n}}{a_{n-1}}| \tag{8.108} \]

那么前两个根应该以二次形式保留：

\[P(s)\approx(1+a_{1}s+a_{2}s^2)(1+\cfrac{a_{3}}{a_{2}}s)...(1+\cfrac{a_{n}}{a_{n-1}}s) \tag{8.109} \]

那么要保证上述近似合理，就要满足如下前提：

\[|\cfrac{a_{2}^2}{a_{3}}|>>|a_{1}|>>|\cfrac{a_{3}}{a_{2}}|>>|\cfrac{a_{4}}{a_{3}}|>>...>>|\cfrac{a_{n}}{a_{n-1}}| \tag{8.110} \]

如果以上的近似均不满足，那么就可能存在三个以上的根并没有相距很远，这时就要使用三次或更高阶次的形式。

例如，考虑图8.30所示的阻尼EMI滤波器。通常将这类滤波器放置在变换器电源输入处以衰减变换器输入电流中的开关成分。通过电路分析，可以证明滤波器的传递函数如下所示：

\[G(s)=\cfrac{i_{g}(s)}{i_{c}(s)}=\cfrac{1+s \cfrac{L_{1}+L_{2}}{R}}{1+s \cfrac{L_{1}+L_{2}}{R}+s^2L_{1}C+s^3\cfrac{L_{1}L_{2}C}{R}} \tag{8.111} \]

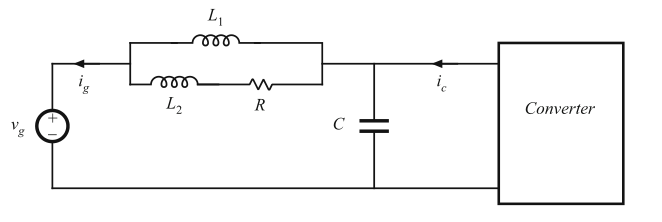
Fig. 8.30 Input EMI filter example

该传递函数包含一个三阶分母，其系数如下所示：

\[\begin{aligned} & a_{1}= \cfrac{L_{1}+L_{2}}{R} \\ & a_{2}= L_{1}C \\ & a_{3}= \cfrac{L_{1}L_{2}C}{R} \end{aligned} \tag{8.112} \]

我们期望将分母分解，来获得极点的解析表达式。正确的方法肯定是取决于\(R,L_{1},C\)的数值。当根为实数且分隔较远时，按式(8.104)的形式可以将其分解为：

\[(1+s \cfrac{L_{1}+L_{2}}{R})(1+sRC \cfrac{L_{1}}{L_{1}+L_{2}})(1+s \cfrac{L_{2}}{R}) \tag{8.113} \]

根据式(8.113)，近似需要满足：

\[\cfrac{L_{1}+L_{2}}{R}>>RC \cfrac{L_{1}}{L_{1}+L_{2}}>>\cfrac{L_{2}}{R} \tag{8.114} \]

上式必须在\(L_{1}>>L_{2}\)的情况下才能满足。当\(L_{1}>>L_{2}\)时，式(8.114)可以被简化为：

\[\cfrac{L_1}{R}>>RC>>\cfrac{L_{2}}{R} \tag{8.115} \]

经过近似分解，式(8.113)可以进一步简化为：

\[(1+s \cfrac{L_{1}}{R})(1+sRC)(1+s \cfrac{L_{2}}{R}) \tag{8.116} \]

因此，在这种情况下，传递函数包含三个相距较远的极点。式(8.113)和(8.116)代表了式(8.111)中的分母的近似分解解析式。尽管必须将数值代入公式(8.114)或者(8.115)来证明近似的正确性，但无论如何，我们都可以将式(8.113)和(8.116)表示为\(L_{1},L_{2},R,C\)的解析函数。公式(8.113)和(8.116)是面向设计的，因为它们可以深入了解如何选择元件的值，从而获得给定的指定极点频率。

当式(8.114)的第二个不等式不满足时：

\[\cfrac{L_{1}+L_{2}}{R}>>RC \cfrac{L_{1}}{L_{1}+L_{2}} \not >> \cfrac{L_{2}}{R} \tag{8.117} \]

那么第二和第三个根应该以二次形式保留：

\[(1+s \cfrac{L_{1}+L_{2}}{R})(1+sRC \cfrac{L_{1}}{L_{1}+L_{2}}+s^{2}L_{1}||L_{2}C) \tag{8.118} \]

这个表达式就来自\(k=2\)时的式(8.106)。根据式(8.107)可知上述近似要在如下前提下满足：

\[\cfrac{L_{1}+L_{2}}{R}>>RC \cfrac{L_{1}}{L_{1}+L_{2}}>>\cfrac{L_{1}||L_{2}}{L_{1}+L_{2}} RC \tag{8.119} \]

在式(8.117)的应用中，我们使\(a_{0}\)等于1。(8.119)的不等式简化为：

\[L_{1}>>L_{2},\ \ and\ \ \cfrac{L_{1}}{R}>>RC \tag{8.120} \]

请注意，这里不再需要\(RC>>L_{2}/R\)。式(8.120)意味着可以将因式分解(8.118)进一步简化为：

\[(1+s \cfrac{L_{1}}{R})(1+sRC+s^2 L_{2}C) \tag{8.121} \]

因此，在这种情况下，传递函数包含一个低频极点，并且这个极点与高频的二次极点对相隔较远。同样，因式分解结果表示为元件值的解析函数，因此也是面向设计的公式。

在第一个不等式不满足的情况下：

\[\cfrac{L_{1}+L_{2}}{R} \not>>RC \cfrac{L_{1}}{L_{1}+L_{2}} >> \cfrac{L_{2}}{R} \tag{8.122} \]

那么第一和第二个根将被表示为二次形式：

\[(1+s \cfrac{L_{1}+L_{2}}{R}+s^2 L_{1}C)(1+s \cfrac{L_{2}}{R}) \tag{8.123} \]

这个表达式从式(8.109)而来。式(8.110)给出了上述表示形式的前提：

\[\cfrac{L_{1}RC}{L_{2}}>> \cfrac{L_{1}+L_{2}}{R}>>\cfrac{L_{2}}{R} \tag{8.124} \]

也就是：

\[L_{1}>>L_{2},\ \ \ and\ \ \ RC>>\cfrac{L_{2}}{R} \tag{8.125} \]

在这种情况下，传递函数包含一个低频二次极点对，该二次极点对与高频实极点相距较远。如果上述的近似表示均不成立，那么三个根相距的就都不远。这个时候，我们就得找到其他可以处理这种三次多项式的方法。而包括图8.30所示的输入滤波器的设计将在第17章中介绍。