[Fundamental of Power Electronics]-PART II-7. 交流等效电路建模-7.4 规范电路模型

7.4 规范电路模型

在讨论了推导开关变换器交流等效电路模型的几种方法后，让我们先停下来，说明下这些结果。所有的在 CCM下以PWM工作的DC-DC变换器都具有相似的基本功能。首先，他们在理想情况下，以100%效率对电压或者电流等级进行转换。其次，他们包含对波形的低通滤波器。尽管必须滤除高频开关纹波，但这种滤波也会影响到低频电压和电流的变化。第三，可以通过占空比的变化来控制变换器的波形。

我们期望具有相似物理特性的变换器具有相似的等效电路结构。因此，我们可以定义一个规范电路模型，来正确说明所有这些基本电路。任何在CCM下的采用PWM的DC-DC变换器都可以采用这种规范形式。这就允许我们能够从物理的视角理解，并比较变换器的交流特性。为了能够以通用方式分析变换器的特性而无需参考特定的变换器，后面的几章中我们将使用规范模型。因此，规范模型使我们能够定义和讨论变换器的物理交流特性。

在本节中，将基于物理参数建立规范电路模型。将给出一个说明如何将变换器等效电路转换为规范形式的实例。最后，还将几种基本的理想变换器的规范模型参数制成了表格。

7.4.1 规范电路模型的建立

规范电路模型的物理构成在图7.33中全部给出。变换器具有功率输入端口\(v_{g}(t)\)，控制输入端口\(d(t)\)以及具有相同电压\(v(t)\)的功率输出端口和负载。正如第3章所述，所有的CCM下的PWM DC-DC变换器的基本功能都是对直流电压和电流等级的变换，并且在理想情况下其效率为100%。如图7.33a所示，我们使用理想的直流变压器对这个特性进行建模，该变压器的有效匝比为\(1:M(D)\)，其中\(M\)为变换比，并且其是关于\(D\)的函数。同时，如果需要，可以通过添加电阻或者对其他变换器损耗建模的元件来完善这个模型。

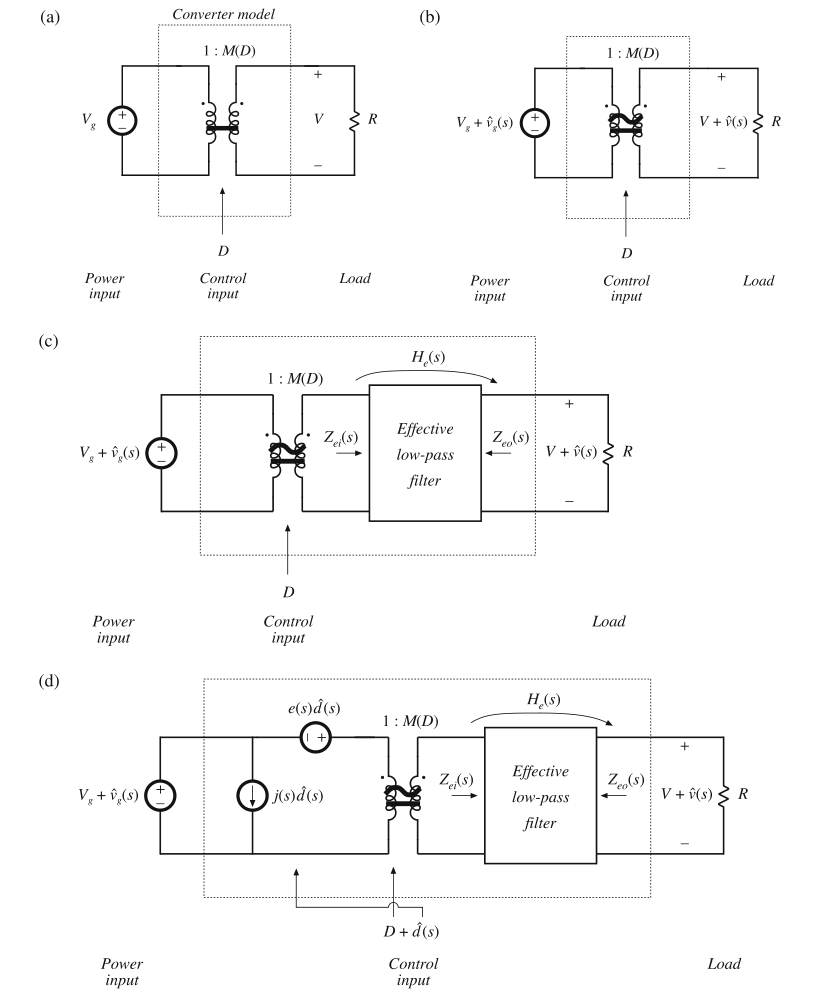
Fig. 7.33 Development of the canonical circuit model, based on physical arguments:(a) dc transformer model, (b) inclusion of ac variations, (c) reactive elements introduce effective low-pass filter, (d) inclusion of ac duty-cycle variations

功率输入电压\(v_{g}(t)\)的缓慢变化会导致变换器输出电压\(v(t)\)的交流变化。如图7.33b所示，我们期望这些变化也可以通过变比\(M(D)\)进行转换。

变换器还必须包括无功元件，来过滤开关谐波和在功率输入输出端口间传递能量。由于希望输出的开关纹波较小，无功元件必须能够形成一个具有截止频率小于开关频率的低通滤波器。这种低通特性还影响着输入电压（译者：原文中为Line voltage，这里认为是直流输入电压）变化对输出电压的关系。因此，模型中还应该包含一个如图7.33c所示的有效的低通滤波器。这个图片预测了输入输出(译者：原文为Line-to-output)的传递函数为：

\[G_{vg}(s)=\frac{\hat{v}(s)}{\hat{v}_{g}(s)}=M(D)H_{e}(s) \tag{7.86} \]

其中\(H_{e}(s)\)为负载电阻为\(R\)时的低通滤波器的传递函数。当负载为非线性时，\(R\)就是静态工作点得到的增量负载电阻(incremental)。滤波器同时还会影响变换器的其他属性，比如小信号输入和输出阻抗。值得注意的是，低通滤波器中的元件值不一定与变换器中的物理元件值相等。通常，滤波器中的元件值，传递函数以及端口阻抗会随静态工作点变化而变化。在下面的章节中给出了示例。

控制输入的变化，特别是占空比\(\hat{d}(t)\)的变化，也会引起变换器电压和电流的交流变化。因此，模型中应该包含由\(\hat{d}(t)\)驱动的电压和电流源。在前节的示例中，我们已经看到了电压源和电流源都出现了，他们分布在电路模型中。可以通过对模型进行处理，从而将所有含\(\hat{d}(t)\)的源整理到等效电路的输入侧。在这个过程中，这些源可能与频率有关；在下一节中将给出一个示例。通常情况下，这些电源可以被组合为如图7.33d所示的单电压源\(e(s)\hat{d}(s)\)和单电流源\(j(s)\hat{d}(s)\)。由这个模型得到的控制到输出的小信号传递函数为：

\[G_{vd}(s)=\frac{\hat{v}(s)}{\hat{d}(s)}=e(s)M(D)H_{e}(s) \tag{7.87} \]

上述式子是在将\(\hat{v}_{g}(s)\)设置为0，求解\(\hat{v}(s)\)与\(\hat{d}(s)\)的关系得到的。图7.33d是一个可以对任何CCM下的PWM DC-DC变换器进行建模的完整的规范电路。

通常，我们对负载电流\(\hat{i}_{load}\)变化引起的输出电压\(\hat{v}\)的变化也比较感兴趣。如图7.34所示，我们可以通过在变换器的输出端添加一个独立电流源来对此进行建模。在图中，负载被建模为并联于独立交流电流源\(\hat{i}_{load}\)的电阻\(R\)。在交流模型中，电阻\(R\)是在静态工作点测得的负载的增量电阻（译者：应该是\(i-v\)曲线的斜率），且\(\hat{i}_{load}\)是负载电流的交流变化量。这个模型得到了从负载电流变化量到输出电压变化量的传递函数为：

\[Z_{out}(s)=-\frac{\hat{v}(s)}{\hat{i}_{load}(s)}=Z_{eo}(s)||R \tag{7.88} \]

为了推导式(7.88)，我们将独立源\(\hat{v}_{g}\)和\(\hat{d}\)置0，求解\(\hat{i}_{load}\)到\(\hat{v}\)的传递函数。这个传递函数（含负号）就是变换器的输出阻抗\(Z_{out}(s)\)。正如上面的定义，输出阻抗包括负载电阻\(R\)的增量。在某些情况下，将输出阻抗\(Z_{out}\)的定义中将负载阻抗去除或者包含其他阻抗可能更为合适。

因此，规范模型可用于求解变换器关键交流传递函数。同时令人感兴趣有控制-输出传递函数\(G_{vd}(s)\)，源-输出传递函数\(G_{vg}(s)\)，以及输出阻抗\(Z_{out}(s)\)。

Fig. 7.34 Modeling the effect of load current variations by addition of independent current source \(\hat{i}_{load}\)

7.4.2 示例：buck-boost变换器模型到规范模型的演化

为了说明规范电路模型的推导步骤，让我们将buck-boost变换器的等效电路演化为规范模型。buck-boost变换器的交流小信号模型在7.2节中已经推导。其结果为图7.16b，这里再次给出，如图7.35所示。为了将这个电路演化为规范形式，有必要将所有关于\(\hat{d}(t)\)的独立源向左移动，同时将电感向右移动从而合并变压器。

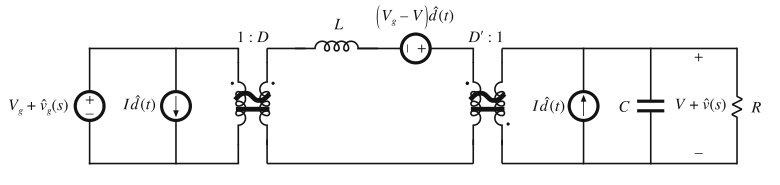
Fig. 7.35 Small-signal ac model of the buck–boost converter, before manipulation into canonical form

电压源\((V_{g}-V)\hat{d}(t)\)与电感串联，因此，这两个元件的位置可以交换。在图7.36a中，电压源被放置在了理想变压器的原边，所以这也就需要将电压除以有效匝比\(D\)。同样的，输出侧电流源\(I\hat{d}(t)\)也被移动到匝比为\(D^{'}:1\)的变压器的原边，这就需要将其乘以匝比\(1/D^{'}\)。其极性也要根据匝比为\(D^{'}:1\)的变压器的极性进行反转。

下一步，我们需要将电流源\(I\hat{d}(t)/D\)移动到电感的左侧。这可以使用图7.36b所示的技巧来实现。电流源的接地点断开，取而代之的是连接到节点\(A\)。另外一个相同的电流源从节点\(A\)连接到地。第二个电流源使流过节点\(A\)的电流并未发生改变，因此图7.36a和7.36b的节点方程是相同的。

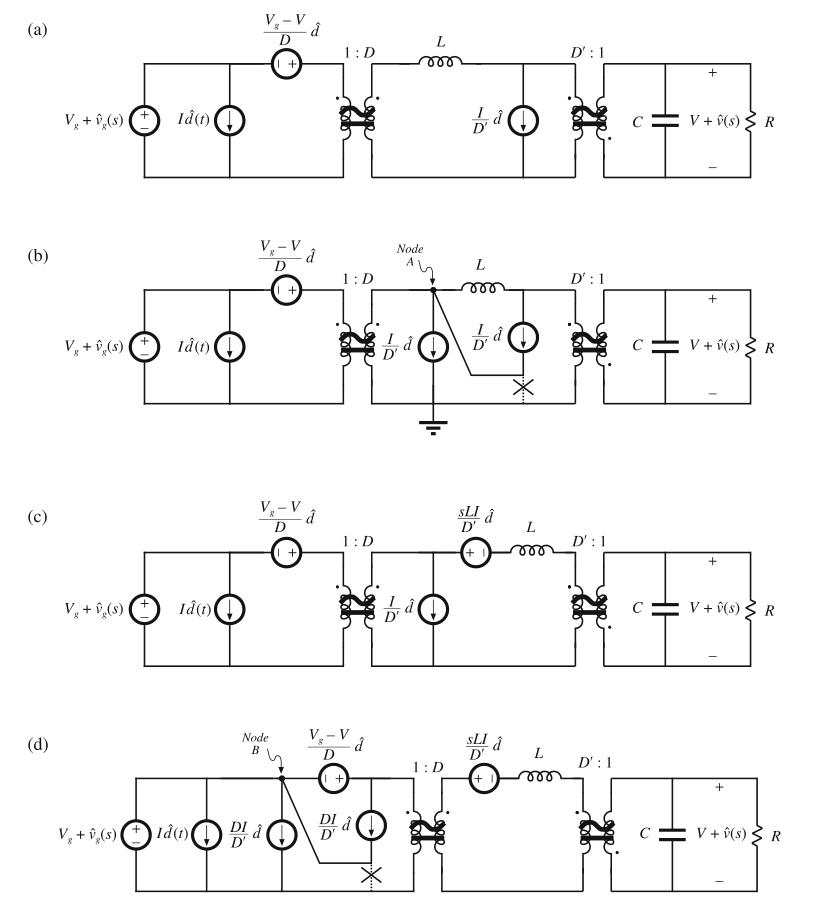
Fig. 7.36 Steps in the manipulation of the buck–boost ac model into canonical form

在图7.36c中，电感和电流源的并联组合被变换为戴维南等效形式。从而获得了电感和电压源的串联组合。

在图7.36d中，电流源\(I\hat{d}(t)/D\)被移到变比为\(1:D\)的变压器的原边。电流源幅值需要乘以变比\(D\)。此外，还可以利用之前的方法，将电流源经电压源\((V_{g}-V)\hat{d}(t)/D\)移动到左侧。电流源的接地点移动到节点\(B\)，并且再添加一个相同的电流源连接到节点\(B\)和地之间。

图7.37就是模型的最终形式。通过乘以匝比的平方，电感被移动到匝比为\(D^{'}:1\)的变压器的次级。通过除以匝比\(D\)，电压源\(sLI\hat{d}(t)/D^{'}\)被移动到匝比为\(1:D\)的变压器的初级侧。如图所示，电压源和电流源可以被组合，将两个变压器组合为一个变比为\(D^{'}:D\)的变压器。电路现在就是规范形式了。

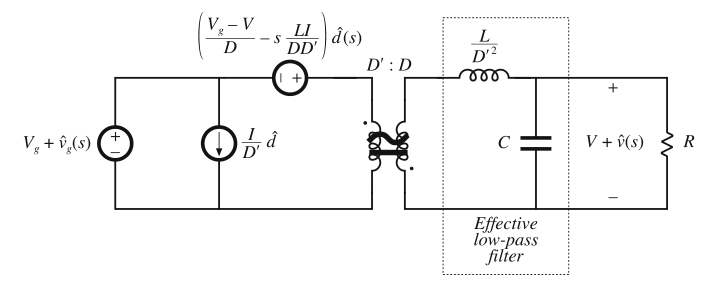
Fig. 7.37 The buck–boost converter model, in canonical form

可以看出，低通滤波器的电感值并不简单的等于物理电感值\(L\)，而是等于\(L/D^{'2}\)。在不同的\(D^{'}\)的不同静态工作点时，这个电感值将会发生变化。因此，低通滤波器的传递函数，输入阻抗和输出阻抗也会随着静态工作点的变化而变化。这种变化的原因就是匝比为\(D^{'}:1\)的变压器对电感值的变化。

同时还可以从图7.37看出，由\(\hat{d}(t)\)引起的电压源的系数为：

\[e(s)=\frac{V_{g}-V}{D}-s \frac{LI}{DD^{'}} \tag{7.89} \]

通过将式(7.30)的直流关系代入后，上式可以简化为：

\[e(s)=- \frac{V}{D^{2}} (1-s \frac{DL}{D^{'2}R}) \tag{7.90} \]

当我们将输出侧电流源\(I\hat{d}(t)\)经过电感移动时，我们获得了一个与频率相关的电压源。因此,\(e(s)\hat{d}\)电压源是频率相关的。

7.4.3 常见变换器的规范电路参数值

对于包含单电感和单电容的理想CCM下PWM DC-DC变换器，其低通滤波器的规范模型应该包含单个电感和单个电容。将规范电路模型可简化为图7.38所示。假设电容直接连接在负载上。对于基本的buck，boost以及buck-boost变换器的参数如表7.1所示。同时再次说明，电感有效值并不等同于物理电感值，其与静态工作点占空比\(D\)是相关的。此外，流过有效电感\(L_{e}\)的电流通常与物理电感器中流过的电流\(I+\hat{i}(t)\)并不相同。

Table 7.1 Canonical model parameters for the ideal buck, boost and buck–boost converters

可以使用传统的线性电路的分析方法来求解图7.38的模型，从而获得感兴趣的关系，如传递函数，输入输出阻抗等。变压器隔离版本的buck，boost以及buck-boost（如全桥，正激和反激变换器）也可以使用图7.38和表7.1的模型和参数进行建模，只是这要在正确考虑变压器匝比的前提下完成。