[Fundamental of Power Electronics]-PART II-7.交流等效电路建模-7.1 引言

7.1 引言

变换器系统总是需要反馈的。例如，在典型的DC-DC变换器应用中，无论输入电压\(V_{g}(t)\)和输出有效负载\(R\)如何变化，都必须使输出电压\(v(t)\)保持恒定。这是通过构建一个可以改变变换器控制输入的回路来完成的[例如：占空比\(d(t)\)]，来使得输出电压\(v(t)\)被调节为期望值\(V_{ref}\)。在逆变器系统中，反馈回路使得输出电压遵循正弦曲线参考电压。在现代低谐波整流系统中，控制系统使得变换器的输入电流与输入电压成正比。从而使得输入端口对于交流电源而言可等效为电阻负载。因此，通常情况下都会使用反馈。

图7.1给出了一个典型的DC-DC系统，其结合了Buck变换器和反馈控制环路。其期望设计出这样一个反馈，使得输出电压可以得到精确调节，并且对\(v_{g}(t)\)和负载电流的变化不敏感。此外，反馈系统应该是稳定的，并且瞬态过冲，建立时间和调节时间等特性应该符合相关的规范要求。本书的第二部分主题就是变换器及其控制系统的交流建模和设计。

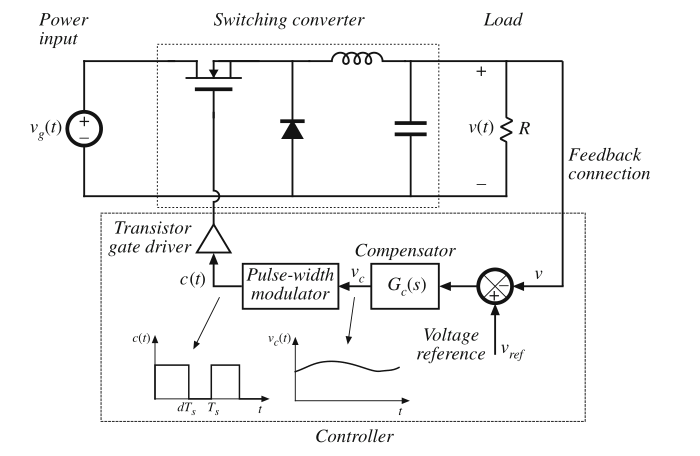
Fig 7.1 A simple DC-DC regulator system, including a buck converter power stage and a feedback network.

为了设计图7.1的系统，我们需要开关变换器的动态模型。电源输入电压，负载电流或者占空比是如何影响输出电压的呢？什么是小信号传递函数？为了回答这些问题，我们将通过引入电感和电容的动态特性来扩展在第2和第3章中得到的稳态模型。可以使用与第2和第3章中非常相似的方法对在CCM下运行的变换器进行动态建模。由此产生的交流等效电路与第3章中得到的直流等效电路非常相似。

建模就是通过数学的手段对物理现象的表示。在工程上，通常希望忽略一些无关紧要的现象的同时，对系统的重要行为特性进行建模。可以完全忽略系统响应的许多方面，也就是这部分内容为“未建模”的，仅使用简化的元件构建端口方程。简化的模型可以得到对系统行为的物理观察，这有助于工程师设计系统来实现指定方式运行。因此，建模过程就涉及到使用近似来忽略较小但比较复杂的现象，来尝试了解最重要的内容。当这种基本了解已经有了以后，就可能需要通过考虑一些以前被忽视的现象来完善模型。实际上，真实的物理系统非常复杂，对其详细的分析很容易得到一些难以处理并且毫无用处的数学混乱结果。近似模型是获得理解和物理描述的重要工具。

如第2章所述，在设计良好的以CCM工作的变换器中，开关纹波很小。因此我们应该忽略开关纹波，仅对变换器波形中潜在的交流变化建模。例如，假设将交流变化引入变换器的控制信号\(v_c(t)\)，使得：

\[v_{c}(t)=V_{c}+V_{cm}cos\omega_{m}t \tag{7.1} \]

其中\(V_{c}\)和\(V_{cm}\)为常数，\(|V_{cm}|<<V_{c}\)，调制频率\(\omega_{m}\)远小于变换器开关频率\(\omega_{s}=2\pi f_{s}\)。该控制信号被馈送到脉冲宽度调制器（PWM）并产生一个开关频率为\(f_{s}=1/T_{s}\)的栅极驱动信号，并且每个开关周期的占空比取决于该开关周期施加的控制信号\(v_{c}(t)\)。

最终的晶体管驱动信号如图7.2(a)所示，典型buck-boost变换器电感电流\(i_{L}(t)\)输出电压波形\(v(t)\)如图7.2(b)所示。\(v(t)\)的频谱如图7.3所示。该频谱包含了开关频率及其谐波和边带成分。如果开关纹波较小，则这些分量的幅值就较小。此外，频谱在调制频率\(\omega_{m}\)处包含一个低频分量。该分量的大小和相位不仅取决于占空比的变化，还取决与变换器的频率响应。如果我们忽略了变换器开关纹波，其低频分量依然存在（如图7.2(c))。我们交流建模工作的目标就是预测这个低频分量。

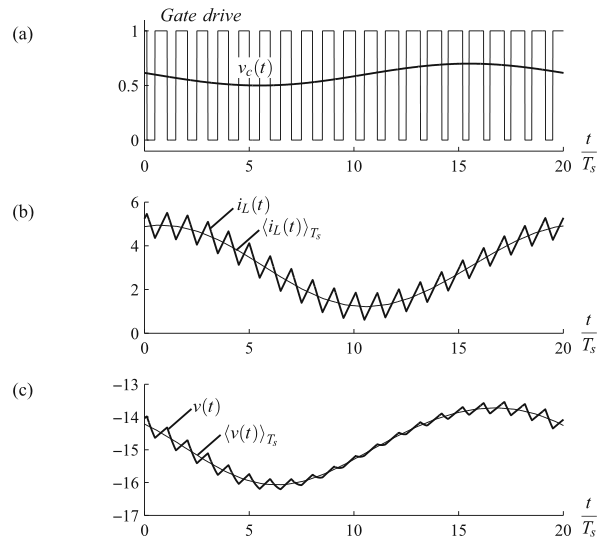
Fig 7.2 AC variation of the converter signals

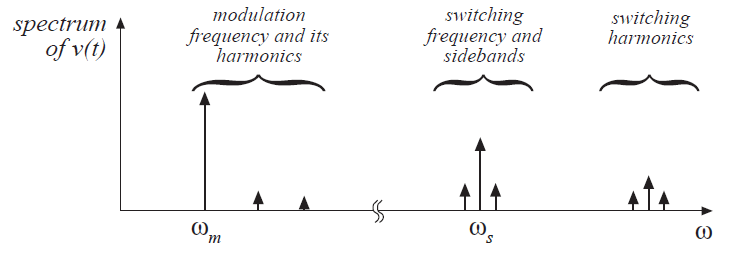
Fig 7.3 Specturm of the output voltage waveform \(v(t)\) of Fig 7.2

在7.2节中介绍了一种推导CCM变换器小信号模型的简单方法。通过平均一个开关周期可以消除电感电流和电容电压的开关纹波。因此，电感和电容波形低频分量通过以下形式的方程进行建模：

\[L \frac{{d<i_{L}(t)>}_{T_{s}}}{dt}=<v_{L}(t)>_{T_{s}} \\ C \frac{{d<v_{C}(t)>}_{T_{s}}}{dt}=<i_{C}(t)>_{T_{s}} \tag{7.2} \]

其中\(<x(t)>_{T_{s}}\)是\(x(t)\)在整个\(T_{s}\)时间长度内的平均值：

\[<x(t)>_{T_{s}}= \frac{1}{T_{s}} \int _{t} ^{t+T_{s}} x(\tau)d\tau \tag{7.3} \]

因此，我们将采用一种基本的近似方法，也就是通过平均一个开关周期来消除高频纹波。从而允许平均值从一个开关周期到下一个开关周期变化，来对低频变化进行建模。实际上，式7.3的移动平均值构成了对波形的低通滤波。本章末尾列出了有关变换器平均建模的众多参考文献中的一部分。（具体参见原文）。

请注意，在变换器工作于稳态时电感伏秒平衡和电容电荷平衡的原理可以用来预测式7.2右侧为0。式7.2描述了在一个开关周期内施加非零平均电感电压和电容电流时，电感电流和电容电压如何变化。式7.2的平均电感电压和电容电流通常是变换器中信号的非线性函数，因此式7.2构建了一组非线性微分方程。实际上，图7.3还包含调制波频率\(\omega_{m}\)的谐波。在大多数变换器中，随着调制频率\(\omega_{m}\)接近开关频率\(\omega_s\)或者调制幅值\(D_{m}\)接近静态占空比\(D\)，这些谐波的幅值会变得很大。非线性元素在电气工程中并不罕见。实际上所有的半导体器件都表现出非线性行为。为了获得易于分析的线性模型，我们通常构建一个围绕静态工作点进行线性化的小信号模型，其中忽略了调制或者激励频率的谐波。例如，图7.4说明了图7.4(b)所示的熟悉的二极管的\(i-v\)特性的线性化。假设二极管电流\(i(t)\)具有静态（DC）值\(I\)和一个信号分量\(\hat{i}(t)\)。因此，二极管两端电压\(v(t)\)就是包含晶体电压\(V\)和信号分量\(\hat v(t)\)。如果信号分量相比静态值非常小：

\[|\hat v|<<|V|,\ |\hat i|<<|I| \tag{7.4} \]

然后，\(\hat v(t)\)和\(\hat i(t)\)之间的关系就是近似线性的，\(\hat{v}(t)=r_{D} \hat{i}(t)\)。电导\(1/r_{D}\)代表了静态工作点处二极管特性的斜率。图7.4(c)的小信号等效电路模型描述了静态工作点附近微小变化时二极管的特性。

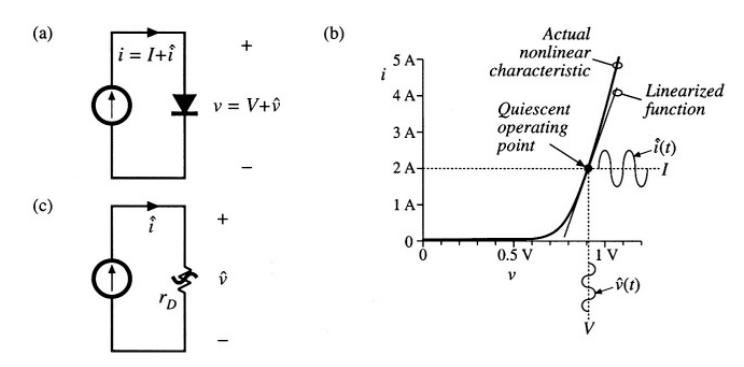
Fig 7.4 Small-signal equivalent circuit modeling of the diode: (a) a nonlinear diode conducting current i; (b) linearation of the diode characteristic around a quiescent point; (c) a linearized small-signal model.

非线性变换器特性的一个示例是buck-boost变换器的稳态输出电压\(V\)与占空比\(D\)之间的关系，如图7.5所示。假定变换器工作在一定的直流输出电压下，比如\(V=-V_{g}\)，其对应的静态占空比就是\(D=0.5\)。关于该静态值的占空比的变化量\(\hat{d}\)将激发出输出电压中的变化量\(\hat{v}\)。如果占空比变化的幅值足够的小，那么我们可以通过线性化曲线来计算最终的输出电压变化。图7.5中线性化特性的斜率与实际非线性特性曲线在静态工作点的斜率相同；这个斜率就是该变换器的“控制-输出”直流增益。如果占空比的变化\(\hat{d}\)足够的小，则线性化和非线性特性的值将会近似相等。

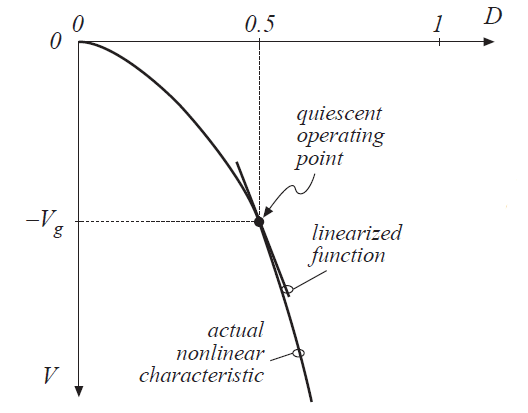
Fig 7.5 Linearization of the static control-to-output charateristic of the buck-boost converter about the quiescent operating point \(D=0.5\).

尽管上述说明了小信号线性化的过程，但图7.5的buck-boost示例过分简化了。变换器的电感和电容使得增益呈现对频率的响应关系。为了正确预测小信号传递函数的零极点，我们必须线性化式7.2中变换器的平均微分方程。这将在7.2节中完成。通过应用第3章中的方法，我们可以建立小信号交流等效模型。图7.6给出了buck-boost变换器的小信号模型；可以使用常规电路分析方法来求解该模型，从而找到小信号传递函数，输出阻抗以及其他与频率相关的特性。在图7.1所示系统中，可以插入等效电路模型来替代原本的变换器。当插入其他系统部分的小信号模型(例如脉冲宽度调制器)时，便获得了完整的线性系统模型。可以使用标准线性技术（例如Laplace变换）来分析该模型，以深入了解系统的行为和特性。

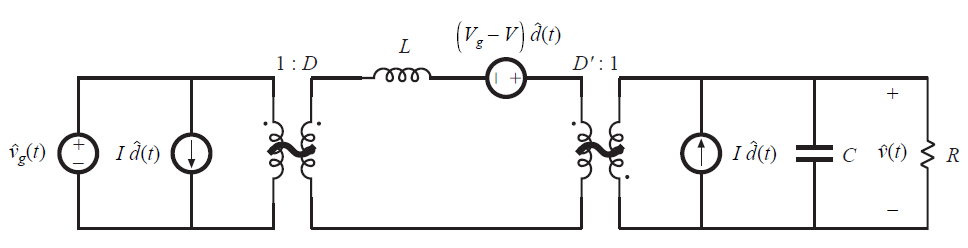
Fig 7.6 Small-signal AC equivalent circuit model of the buck-boost converter.

在7.5节和第14章中，将介绍交流建模方法的两个众所周知的变体，状态空间平均和电路平均。在14章中还讨论了电路平均的扩展，也就是平均开关建模。由于开关是唯一引入开关谐波的元件，因此可以通过仅对开关波形进行平均来得到等效电路模型。只需要将开关替换为平均开关模型，即可获得适用于分析或仿真的变换器模型。平均开关建模可以扩展到其他工作模式，例如不连续导通模式，以及电流编程控制和谐振变换器。在7.4节中，说明了可以以标准形式编写任何DC-DC脉宽调制CCM变换器的小信号模型。这种等效电路称为规范模型，其描述了这些变换器可能表现出的基本物理特性。7.3节描述了脉宽调制电路的简化模型。

如果你不知道如何应用这些模型，那他们将毫无用处。所以，在第8章中，以面向设计和详细的方式探讨了变换器的频率响应。基本的变换器小信号传递函数被制成表格。变换器传递函数和阻抗的伯德图以简单和近似的方式得到，从而可以深入了解复杂变换器系统的频率响应的来源。

这些结果将应用于设计第9章中的变换器控制系统和第17章中的输入滤波器。在第15和第18章中扩展了建模技术，包括了不连续导通模式和电流编程模式。